Математика формулалары жинағы: үшбұрыштар, төртбұрыштар, шеңбер және квадрат теңдеулер


Тәжірибе стансасының негізгі мектебі
Формулалар жинағы
Математика пәнінің мұғалімі
Құдайберген Бисен Жетпісбай Ұлы
2013 жылы

Аты жөні: Бисен Құдайберген Жетпісбай Ұлы
Туған жылы. айы күні: 1954 жылы 13 қазан
Бітірген оқу орыны: Ақтөбе педагогикалық институты
Мамандығы: Математика пәнінің мұғалімі
Білімі: Жоғары
Жалпы педагогикалық өтілі: 36 жыл
Мекен жайы : Мұғалжар ауданы
Жұрын стансасы
Тәжірибе стансасы ауылы
Жастар көшесі № 5 үй
Сот 8 - 701 - 385 - 2 - 385
I. ТІКБҰРЫШТЫ ҮШБҰРЫШ
 a, b - катетер, c - гипотенуза.
a, b - катетер, c - гипотенуза.
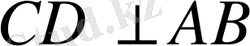 , h - биіктік,
, h - биіктік,
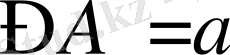
C
b a
h
A B
D
 Equation. 3
Equation. 3
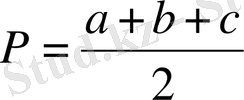 - жарты периметр.
- жарты периметр.
1. b 2 = c · c b
a 2 = c · c a
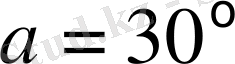 болса, онда
болса, онда
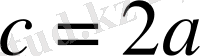
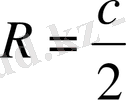
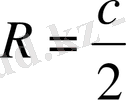 Формуласымен анықталады
Формуласымен анықталады
6.
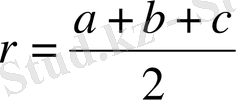
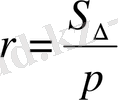
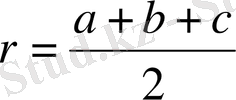 және
және
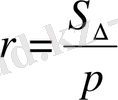 формуласымен анықталады
формуласымен анықталады
7.
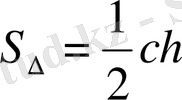
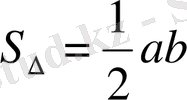
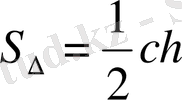 және
және
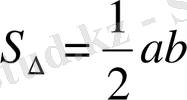 формулаларымен анықталады
формулаларымен анықталады
II. Қиғашбұрышты үшбұрыш
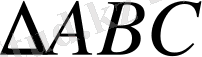
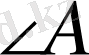 ;
;
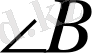 - сүйір бұрыштар, СD - биіктік, АВ - табаны.
- сүйір бұрыштар, СD - биіктік, АВ - табаны.
a 2 = c 2 + b 2 - 2cc b
b 2 = c 2 + a 2 - 2cc a
Cүйір бұрышқа қарсы жатқан қабырғаның квадраты, былайғы екі қабырғасы квадраттарының қосындысының табаны мен бүйір қабырғасының табанындағы проекциясының екі еселенген көбейтіндісін азайтқанға тең.
С
b a
h
А c b c a В
D
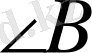 - доғал бұрыш b
2
= a
2
+ c
2
+2a
1
c Доғал бұрышқа қарсы жатқан квадраты, былайғы екі қабырғасы квадраттарының қосындысына табаны мен екінші бүйір қабырғасының табанындағы проекциясының екі еселенген көбейтіндісін қосқанға тең
- доғал бұрыш b
2
= a
2
+ c
2
+2a
1
c Доғал бұрышқа қарсы жатқан квадраты, былайғы екі қабырғасы квадраттарының қосындысына табаны мен екінші бүйір қабырғасының табанындағы проекциясының екі еселенген көбейтіндісін қосқанға тең
C
b a
h
D
А c B a 1
Ауданды анықтайтын формулалар
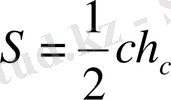 ,
,
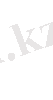
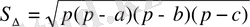 ,
,
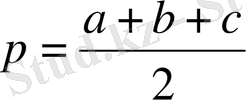 .
.
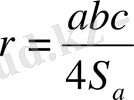 ,
,
S a - ауданы
Сыртай сызылған шеңбердің центрі қабырғаларынығ орта перпендикулярларының қиылысу нүктесінде жатады да, радиусы
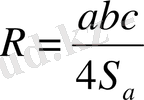 формуласымен анықталады
формуласымен анықталады
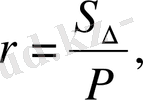 S - ауданы
S - ауданы
p - жарты периметр
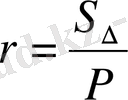 формуласымен анықталады
формуласымен анықталады
Бисектрисаны есептеу формулалары
С
b l c a
А В
b 1 D a 1
Үшбұрыштың ішкі бұрышының биссектрисасы табанын іргелес қабырғаларына пропорционал бөліктерге бөлінеді: l c -биссектриса
a)
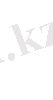
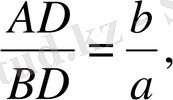 б)
б)
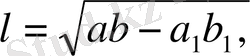
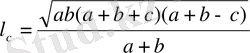
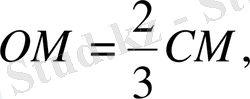
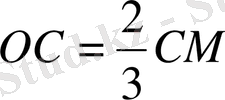
C
a
o N
A B
M
AN, CM - медианалар. Үшбұрыштың медианалары бір нүктеде қиылысады жіне төбесінен бастап есептегенде сол нүктеде 2 : 3 қатынасында бөлінеді.
Медиана
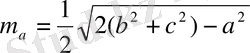 формуласымен есептеледі
формуласымен есептеледі
h a, h b, h c - cәйкес қабырғаларына түсірілген биіктік

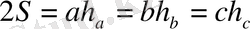 формулаларын пайдаланып тапсақ:
формулаларын пайдаланып тапсақ:
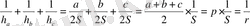
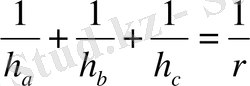 :
:
r - іштей сызылған шеңбер радиусы
III. ТӨРТБҰРЫШТАР
B
A O C
D
Ромб
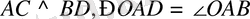
Ромбының диогналдары өзара перпендикуляр және бұрыштарын қақ бөледі
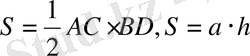 Ромбының ауданын есептейтін формулалар
Ромбының ауданын есептейтін формулалар
A B
o
b h
D C
ПАРАЛЛЕЛОГРАММ
AC 2 + BD 2 = 2a 2 + 2b 2
Диогналдарының киадраттарының қосындысы, оның барлық қабырғаларының киадраттарының қосындысына тең
Ауданы S = ah формуласымен анықталады
B b C
M h K
A D
a
Трапеция
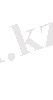
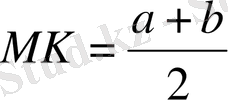 ; Трапециярың орта сызығы табандарының қосындысының жартысына тең
; Трапециярың орта сызығы табандарының қосындысының жартысына тең
Ауданы
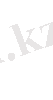
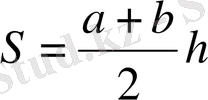 формуласымен анықталады
формуласымен анықталады
b
B C
c d
• O
A B
a
Трапеция
a +b = c+d. Егер трапецияға іштей шеңбер сызылған болса, онда табандарының қосындысы бүйір қабырғаларының қосындысына тең болады
M
B C
o
A D
N
Трапеция
Диогналдары өзара перпендикуляр болатын тең бүйірлі трапециярың ауданы - биіктігінің квадратына тең
S = h 2
B b C
c •o c
A D
Трапеция
Теңбүйірлі трапецияға іштей шеңбер сызылатын болса, онда биіктігі табандарының геометриялық орташасы болады:
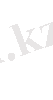
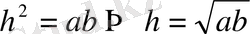
IV ШЕҢБЕР ЖӘНЕ ДӨҢГЕЛЕК
B
1 A
2
C
AB=AC
 Equation. 3
Equation. 3
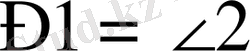 Егер щеңберден тысқары жатқан нүктеден оған екі жанама жүргізсе, онда:
Егер щеңберден тысқары жатқан нүктеден оған екі жанама жүргізсе, онда:
a) берілген нүктеден жанасу нүктесіне дейінгі кесінділердің ұзындықтары тең;
б) центрден өтетін қиюшымен жанамалар арасындағы бұрыштар өзара тең.
B n 1 A
n
D
b
c d b
a
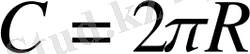
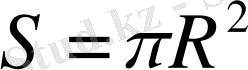
В
А
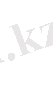
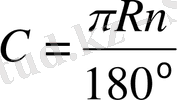
о
r • r
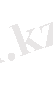
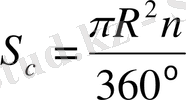
•о
a
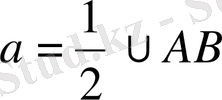
C D
A • B
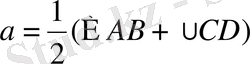
A E
B M
C
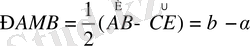
B D
A
•O
E
C
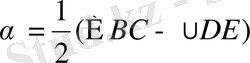
1 - ден 10 - ға дейінгі натурал сандардың квадраттары және кубтары
2 және 3 сандарының дәрежелері
10 - нан 99 - ға дейінгі натурал сандардың квадраттарының кестесі
Ондық-
тар
ҚЫСҚАША КӨБЕЙТУ ФОРМУЛАЛАРЫ
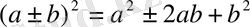
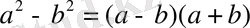
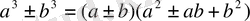
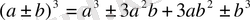
НАТУРАЛ ЖӘНЕ БҮТІН КӨРСЕТКІШТІ ДӘРЕЖЕНІҢ ҚАСИЕТТЕРІ


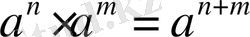
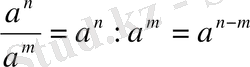
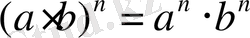
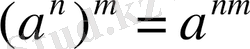
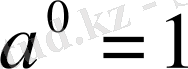
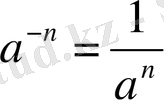
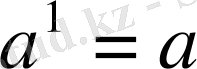
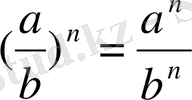
Бөлшек өрнектерге амалдар қолдану
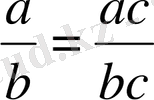
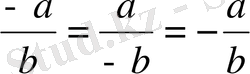
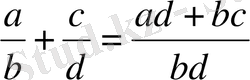
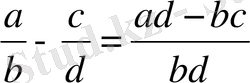
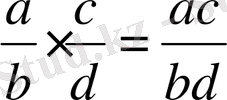
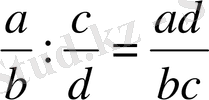
Тригонометриялық функциялардың мәндерінің кестесі
0
( 0˚)
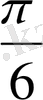
(30˚)
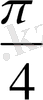
(45˚)
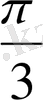
(60˚)
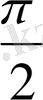
( 90˚)
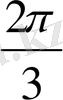
(120˚)
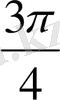
(135˚)
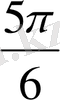
(150˚)

(180˚)
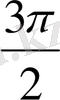
(270˚)

(360˚)
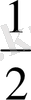
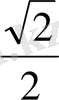
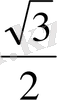
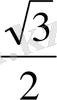
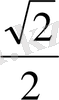
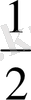
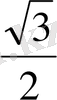
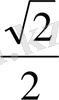
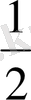
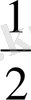
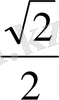
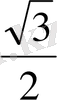
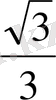
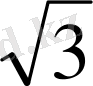
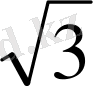
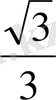
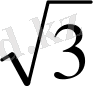
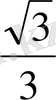
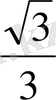
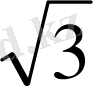
Келтіру формулалары
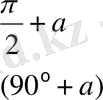
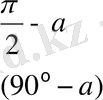
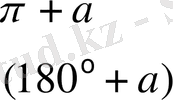
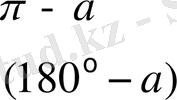
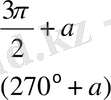
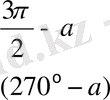
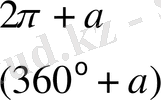
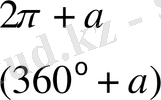
Негізгі тригонометриялық тепе - теңдіктер
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz