10-сынып математикасы: 4 нұсқа, әр нұсқа 25 есеп


10 сынып №1
1. Квадраттың қабырғалары 25%-ке ұзартылған. Квадраттың ауданы қанша процентке көбейеді?
2. Теңдеуді шешіңіз: 5 - 3(x - 2(x - 2(x - 2) ) ) = 2.
3. Бөлшектің бөліміндегі иррационалдықтан құтылыңыз:
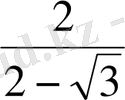 .
.
4. Теңсіздіктер жүйесін шешіңіз:
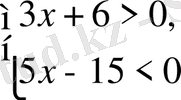
5. у-ті х арқылы өрнектеңіз: 2х + 5у - 16 = 0.
6. Жазықтықта тік бұрышты үшбұрыш берілген, гипотенузасы 12 см. Кеңістікте берілген бір нүктеден үшбұрыш төбелеріне дейінгі қашықтық 10 см-ден. Үшбұрыш жазықтығынан кеңістіктегі нүктеге дейінгі қашықтықты табыңыз.
7. Квадраттың диагоналі 4см. Бұл квадраттың қабырғасы басқа квадраттың диагоналі болып табылады. Екінші квадраттың қабырғасын табыңыз:
8. Ромбының биіктігі 10см, ал сүйір бұрышы 30 0 -қа тең деп алып, оның ауданын табыңыз:
9.
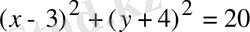 шеңбердің центрінен координаттар басына дейінгі ара қашықтықты табыңыз
шеңбердің центрінен координаттар басына дейінгі ара қашықтықты табыңыз
10. Есептеңіз:
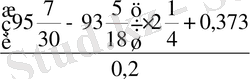
11. Теңдеуді шешіңіз: 1 - 4sіn 2 x = 0
12. Сырттай жанасатын екі дөңгелектің аудандарының қосындысы
130π см 2 . Егер олардың центрлерінің ара қашықтығы 14 см-ге тең болса, онда олардың радиустары неге тең?
13. Теңсіздіктің дұрыс шешімін анықтаңыз:
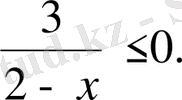
14. Интегралды есептеңіз:
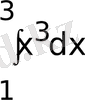
15. Геометриялық прогрессияның мүшелері оң S2 = 4, S3 = 13 екені белгілі болса, онда S4 есептеңіз.
16. Есептеңіз:
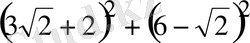 .
.
17. Теңдеулер жүйесін шешіңіз:
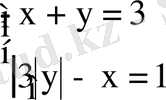
18. f(х) = х
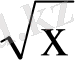 функциясының туындысын табыңыз.
функциясының туындысын табыңыз.
19. Функцияның туындысын тап
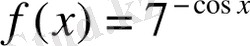
20. Үш учаскенің ауданы 60га. Бірінші учаскенің ауданы барлығының ауданының 25%-не тең. Екінші және үшінші учаскелердің аудандарының қатынастары 4:5-ке қатынасындай. Учаскелердің әрқайсысының ауданын табыңыз.
21. Теңдеулер жүйесін шешіңіз:
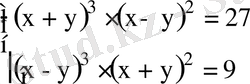
22. Теңдеулер жүйесі
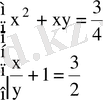 болса, х⋅у неге тең?
болса, х⋅у неге тең?
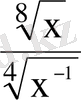 .
.
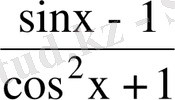 = 0.
= 0.
10 сынып №2
1. Күніне жылқыларға 96 кг шөп беретіндей етіп шөп қоры дайындалды. 2 жылқыны көрші колхозға өткізгендіктен, күніне әр жылқыға беретін тиісті мөлшерлі шөпті 4 кг-ға артық беруге тура келді. Әуелде қанша жылқы болып еді?
2. 6 күннің ішінде 24 адам құлпынай салынған учаскенің шөбін жұлды, онда 36 адам сол жұмысты неше күнде орындайтынын табыңыз:
3. Теңдеуді шешіңіз: 100 - 20y = -y 2
4. Ықшамдаңыз:
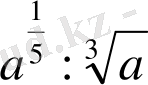
5. Функцияның анықталу облысын табыңыз: у =
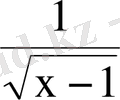
6. C бұрышы тік болатын тік бұрышты АВС үшбұрышында АС катеті 2-ге тең, гипотенузасы АВ=4. В төбесінен жүргізілген үшбұрыштың медианасын табыңдар.
7. Трапецияның орта сызығы 7см тең, ал табандарының бірі екіншісінен 4см-ге артық. Трапецияның табандарын табыңдар.
8. Ауданы қабырғаларының ұзындығы 8м және 18м тік төртбұрыштың ауданына тең болатын квадраттың қабырғасын табыңыз:
9. Қиық конустың табан радиустары 7 м және 4 м, жасаушысы табанына 60° бұрышпен көлбеген. Жасаушысын табыңыз.
10. Клоунға санды айтты да, оны 0, 5-ке көбейтіп, нәтижеге 3 қосу керек деді. Клоун шатастырып, берілген санды 0, 5-ке бөліп, нәтижеден 3-ті шегерді. Клоун шатысса да, егер дұрыс жауабын берген болса, оған қандай сан айтылды?
11. Теңдеуді шешіңіз: x = -3x - 5.
12. Екі санның геометриялық ортасы кішісінен 12-ге артық, ал сол сандардың арифметикалық ортасы үлкенінен 24-ке кем. Осы сандарды табыңыз.
13. Пропорцияның белгісіз мүшесін табыңыз: 18:х=7, 2:4, 5
14. Ықшамдаңыз:
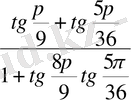 - 1.
- 1.
15. Сөйлемді аяқтаңыз:
“Синус пен косинус функцияларының анықталу облысы - . . . ”.
16. Теңдеулер жүйесін шешіңіз:
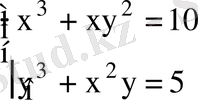
17. f(х) = 3sіn7х функциясының туындысын табыңыз.
18. Фунциясының туындысын тап:
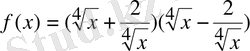
19. A(3; -4) нүктесінен өтетін, центрі координаттар басында орналасатын шеңбердің теңдеуін көрсетіңіз:
20. Егер өспелі геометриялыќ прогрессияны ќұрайтын үш санның ортанғысын екі есе көбейтсе, онда арифметикалыќ прогрессия шығады. Геометриялыќ прогрессияның еселігін табыңыз
21. Теңдеуді шешіңіз: 2 sіn x + cos x =1
22. Теңдеулер жүйесін шешіңіз:
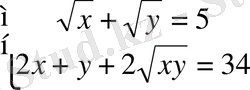
23. Теңсіздіктер жүйесін шешіңіз:
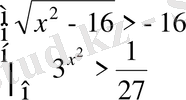
24. ϕ(x) = xe -3x функциясының өсу аралығын табыңыз.
25. Теңсіздікті шешіңіз: х 2 + x < x(x + 5) + 5.
10 сынып №3
1. Әсеттің массасы 35 кг. Адам массасының 65%-і су. Әсеттің денесінде неше килограмм су бар?
2. Теңдеуді шешіңіз:
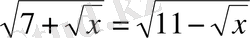 .
.
3.
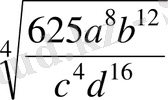 түбірін табыңыз және оның a = 1, b = 3, c = 5, d = 3 деп алғандағы сан мәнін есептеңіз.
түбірін табыңыз және оның a = 1, b = 3, c = 5, d = 3 деп алғандағы сан мәнін есептеңіз.
4. Теңсіздіктер жүйесін шешіңіз:
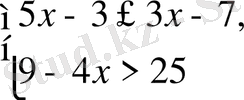
5. 2x- y= 11 теңдеуінің графигінің ординатасы нөлге тең, нүктесінің абсциссасын табыңыз:
6. АВС үшбұрышының АС қабырғасына параллель DK кесіндісі жүргізілген (кесіндінің D ұшы АВ қабырғасында, ал K ұшы ВС қабырғасында жатыр ) . АB = 8 см, АС =10 см және DK = 7, 5 см деп алып, AD кесіндісін табыңдар.
7. Ромбының бір қабырғасының диагональдармен жасайтын бұрыштарының қатынасы 2:7 қатынасындай. Ромбының бұрыштарын табыңдар.
8. Үшбұрыштың биіктігі мен табаны берілген: h а =10 см, а=5 см. Үшбұрыштың ауданын табу керек.
9. m-нің қандай мәнінде
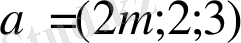 және
және
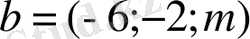
векторларының ұзындығы тең болады?
10. Өрнекті түрлендіріңіз:
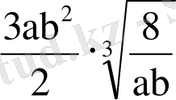 .
.
11. Теңдеуді шешіңіз:
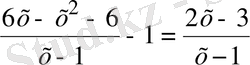
12. Пропорцияның алғашқы үш мүшесінің қосындысы 58-ге тең. Үшінші мүшесі бірінші мүшесінің
 -сін, ал екіншісі
-сін, ал екіншісі
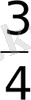 -ін құрайды. Пропорцияның төртінші мүшесін табыңыз.
-ін құрайды. Пропорцияның төртінші мүшесін табыңыз.
13. Теңсіздіктің шешімін табыңыз:
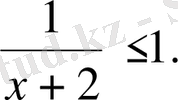
14. Есептеңіз:
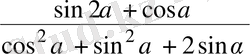 , егер α = -
, егер α = -
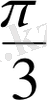 .
.
15. Егер геометриялық прогрессияда b
4
- b
2
= -
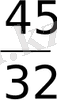 және b
6
- b
4
= -
және b
6
- b
4
= -
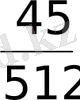 екендігі белгілі болса, онда прогрессияның еселігі мен бірінші мүшесін табыңыз.
екендігі белгілі болса, онда прогрессияның еселігі мен бірінші мүшесін табыңыз.
16. Көбейткіштерге жіктеңіз: (a 2 + b 2 ) 2 - a 2 (a 2 + b 2 ) .
17. Теңдеулер жүйесін шешіңіз:.
:
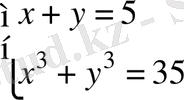
18. f(x) = 2x 4 -x 2 функциясы үшін f ′(x) = 0 теңдеуін шешіңіз.
19. Егер f(x) = sіn
4
x - cos
4
x болса, онда f ' (
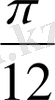 ) мәнін табыңыз.
) мәнін табыңыз.
20. 10 м 3 ауа 13 кг тартады. Ұзындығы 4, 2 м, ені 3, 5 м және биіктігі 2, 6 м болатын бөлмедегі ауа қанша тартады?
21. Теңдеулер жүйесін шешіңіз:
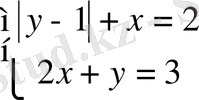
22. Теңдеулер жүйесін шешіңіз:
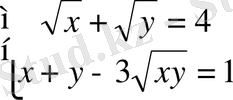
23. у = x -2 ⋅ e 1+2x функциясының графигінің х 0 = -0, 5 нүктесінде жүргізілген жанаманың теңдеуін жазыңыз.
24. Есептеңіз:
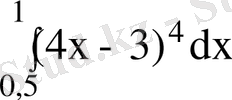 .
.
25. Үшбұрышты дұрыс пирамиданың төбесіндегі жазық бұрышы 90° тең. Бүйір бетінің ауданы 192 см 2 тең пирамиданың бүйір жағына сырттай сызылған шеңбердің радиусын табыңыз.
10 сынып №4
1. Тіктөртбұрыштың ауданы 42 см 2 . Егер оның ені 3 см болса, ұзындығы қанша болады?
2. Теңдеуді шешіңіз: sіn3xcos3x = -
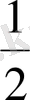 .
.
3. Аэропортта 880 жолаушы ұшақ күтіп отыр. Олардың 35%-і еркектер. Әйелдер мен балалардың жалпы санының 75%-ін әйелдер құрайды. Аэропортта қанша әйел және қанша бала болғанын табыңыз?
4. Бөлшекті қысқартыңыз:
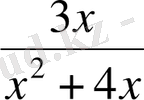 .
.
5. Мына өрнекті оған тең синус функцияның ең кіші оң аргументінің мәнімен алмастырыңыз:
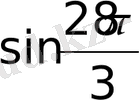
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz