Квадрат теңдеуінің мәні түбірлері

Маңғыстау облысы, Ақтау қаласы
№8 орта мектептің математика мұғалімі
Налибаева Қарлығаш Шамсудинқызы

Сабақтың тақырыбы: «Квадрат теңдеулер» тақырыбын қайталау

Сабақтың мақсаты: Білімділік: Оқушылардың квадрат теңдеулерді шешу
дағдыларын жетілдіру;

Дамытушылық:Оқушылардың ой өрісін кеңейтіп,шығармашылық қабілеттерін
дамыту;

Тәрбиелік:Оқушыларды алғырлыққа, тапқырлыққа, шапшаңдыққа тәрбиелеу;

Сабақтың түрі: қайталау

Сабақтың әдісі:сұрақ-жауап,түрлі тапсырмалар

Сабақтың көрнекілігі:слайдтар

Сабақтың барысы: Ұйымдастыру

Үй тапсырмасын сұрау

Сұрақ-жауап

1. Қандай теңдеуді квадрат теңдеу дейміз?
2. Толық квадрат теңдеу дегеніміз не?
3. Толымсыз квадрат теңдеулер дегеніміз не?
4. Келтірілген квадрат теңдеу дегеніміз не?
5. Теңдеуді шешу дегеніміз не?
6. Теңдеудің түбірі дегеніміз не?
7. Квадрат теңдеу түбірлерінің дискриминантын қалай табамыз?
8. Квадрат теңдеудің түбірлерінің санын қалай анықтаймыз?

|Квадрат теңдеуінің түрлері |Дискриминанттың |Квадрат теңдеуінің |
| |мәні |түбірлері |
|Толымсыз |ax2=0 |- |x1=0, x2=0 |
|квадрат |(b=c=0) | | |
|теңдеулер | | | |
| | | | |
| | | | |
| |ax2+bx=0 |- |x1=0, x2=- |
| |(c=0) | | |
| |ax2+c=0 |- |->0 болғанда, |
| |(b=0) | |x1;2=± |
| | | |-<0 болғанда, |
| | | |теңдеудің шешімі жоқ |
|Толымды |Жалпы түрі: |D>0 |x1;2= |
|квадрат |ax2+bx+с=0, | | |
|теңдеулер |D=b2-4ac | | |
| | | | |
| | | | |
| | |D=0 |x=- |
| | |D<0 |Теңдеудің шешімі жоқ |
| |b=2n |D>0 |x1;2= |
| |ax2+bx+с=0, | | |
| |D=n2-ac | | |
| | | | |
| | |D=0 |x=- |
| | |D<0 |Теңдеудің шешімі жоқ |
| |Келтірілген |D>0 |x1;2=-k |
| |квадрат теңдеуі: | | |
| |x2+px+q=0, | | |
| |мұндағы p=2k | | |
| |D=k2-q | | |
| | |D=0 |x=-k |
| | |D<0 |Теңдеудің шешімі жоқ |

|Теңдеу |a |b |c |D= |Түбірлер |
| | | | | |саны |
| | | | | | |
| | | | | | |
| | | | | | |

Кім жылдам?

Деңгейлік тапсырмалар

I деңгей №360 (1,3)

А) a=-2, b= c=3

Б) a=0,7, b=6 c=-8 болса, теңдеуін жаз

I I деңгей №362 (1,3)

Теңдеуді шешіңдер

А)

Б)

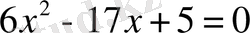
I I I деңгей №365 (1,2)

А)

Б)

Тарихи деректер

Квадрат теңдеуді шешу әдістері Вавилон қолжазбаларында,ежелгі грек
математигі Евклидтің (б.з.д.ІІІ ғ.) еңбектерінде,ежелгі Қытай мен Жапон
трактаттарында кездеседі. Сонымен қатар,Орта Азия математигі әл-Хорезмидің
(ІХ ғ.) «Хисаб әл-джебр вал-мукабала» деген еңбегінде жазылған.Ежелгі
үнді ғалымдары квадрат теңдеуге келтіретін есептерді өмірден алды.Олар мал
санын есептеу,еңбекақы төлеу және т.б.

Кестемен жұмыс

|Түбірлері |Қосындысы |Көбейтіндісі |Теңдеу |
|Х1=-2, X2=3 | | | |
|Х1=5, X2=6 | | | |
|Х1=-4, X2=-3 | | | |
|Х1=1.5, X2=4 | | | |
|Х1=0.6, X2=2 | | | |

Сергіту сәті
Оқулықпен жұмыс

№367 есеп

Сабақты қорытындылау

Рефлексия парағы

Рефлексия: (қорытынды) Оқушылар өз ойларын білдіреді.

Оқушының аты-
жөні:______________________________________________________________

1. Қандай теңдеуді еске
түсірдің?_________________________________________________________

2. Квадрат теңдеудің қандай түрлерін
қайталадың?____________________________________________

3. Квадрат теңдеуді шешіп үйрендің
бе?__________________________________________

4. Деңгейлік тапсырмаларды орындай алдың
ба?__________________________________________________

5. Сабақ ұнады ма? Қандай тілегің
бар?____________________________________________________

Баға:___________________________________________________

Үйге тапсырма

№362 есеп (2,4)

№365 есеп (2, 4)

Бағалау