Толымсыз квадрат теңдеу

Сабақтың тақырыбы: Квадрат үшмүшені көбейткіштерге жіктеу.
Сабақтың мақсаты:
Білімділік: Оқушыларды квадрат үшмүше және оның түбірлері ұғымдарымен
таныстыру, оқушылардың квадрат үшмүшені көбейткіштерге жіктей алу
дағдыларын қалыптастыру.
Дамытушылық: Оқушыларды алғырлыққа, тез ойлай білуге дағдыландыра
отырып, олардың талдау, салыстыра білу, танымдық, өз бетімен еңбектену,
ауызша және жазбаша есептеу қабілеттерін дамыту.
Тәрбиелік: Математика пәні талап ететін ұқыптылыққа, ізденімпаздыққа,
жауапкершілікке тәрбиелеу арқылы оқушылардың меңгерген білімдерін іс-
жүзінде қолдана білуге үйрету, оқушылардың пәнге деген көзқарасын, білімге
деген құштарлығын арттыру.
Сабақтың типі: Жаңа сабақты меңгеру.
Сабақтың түрі: Аралас сабақ.
Оқыту әдіс-тәсілдері: Сұрақ-жауап, практикалық, тест, көрнекілік,
салыстыру.

Сабақ жоспары:
І. Ұйымдастыру бөлімі:
✓ оқушылармен амандасу, оларды түгендеу;
✓ оқушылардың сабаққа дайындығын тексеру;
✓ оқушылар назарын сабаққа аудару;
✓ кері байланыс картасымен таныстыру, сабақ соңында толтыру керектігі
ескертіледі.

ІІ. Үй тапсырмасын тексеру: 1. «Ұшқыр ойдан-ұтымды жауап» сұрақ-жауап
кезеңі:
1. Төртінші дәрежелі теңдеуді шешу үшін не қолданамыз?
Жауабы: Жаңа айнымалыны енгізу арқылы.
2. Квадрат теңдеу дегеніміз не?
Жауабы: ах2+bx+c=0 түрінде берілген теңдеу квадрат теңдеу деп аталады.
3. Толымсыз квадрат теңдеу дегеніміз не?
Жауабы: b мен c нөлге тең болатын дербес жағдайлардағы квадрат теңдеу
толымсыз квадрат теңдеу деп аталады.
Толымсыз квадрат теңдеулер былай жазылады:
1) ах2+bх=0 (мұндағы с=0);
2) ах2+с=0 (мұндағы b=0);
3) ах2=0 (мұндағы b=0, с=0).
4. Квадрат теңдеудің түрлерін ата?
Жауабы: Толымды квадрат теңдеу, толымсыз квадрат теңдеу, келтірілген
квадрат теңдеу.
5. Толымды квадрат теңдеу дегеніміз не?
Жауабы: Егер (1) теңдеудегі b≠0 және c≠0 болса, онда ол толымды квадрат
теңдеу деп аталады. Мысалы: х2-2x-1=0, 3х2-8x+5=0, 2,1х2+102,3x+0,8=0.
6. Квадрат үшмүше дегеніміз не?
Жауабы: ах2+bx+c түрінде берілген теңдеу квадрат үшмүше деп аталады.

2. «Миға шабуыл» кезеңі:

ІІ. Мағынаны тану. Жаңа сабақ:
Алдымен х2+px+q келтірілген квадрат үшмүшесін көбейткіштерге жіктейік.
Бұдан былай х2+px+q=0 квадрат теңдеуінің түбірлерін х2+px+q квадрат
үшмүшесінің түбірлері деп атаймыз. Бұл квадрат үшмүшенің түбірлері
х2+px+q=0 теңдеуінің түбірлерімен бірдей болғандықтан, -(х1+x2)=p, х1∙x2=q
теңдіктері орындалады. Сонда
х2+px+q=х2-(х1+x2)х+х1∙x2=х2-х1х+х1x2=х(х-х1)-х2(х-х1)=(х-х1)(х-х2)теңдігін
аламыз. Сонымен, егер х1 және х2 сандары х2+px+q квадрат үшмүшесінің
түбірлері болса, онда х2+px+q=(х-х1)(х-х2) теңдігі орындалады.
Ал жалпы жағдайда, aх2+bx+c квадрат үшмүшесінің түбірлері aх2+bx+c=0
теңдеуінің немесе 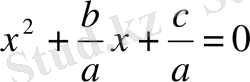теңдеуінің түбірлерімен бірдей болады. Егер оның
түбірлері х1,x2 болса, онда жоғарыдағы көрсетілгендей 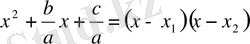теңдігі
орындалады. Сондықтан 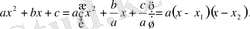Сонымен, егер х1 және x2 сандары aх2+bx+c
квадрат үшмүшесінің түбірлері болса, онда aх2+bx+c=а(х-х1)(х-х2) теңдігі
орындалады.
1-мысал. х2-6x+8 квадрат үшмүшесін көбейткіштерге жіктейік. Оның
түбірлері: х1=2, х2=4 болғандықтан, х2-6x+8=(х-2)(х-4) теңдігін аламыз.
2-мысал. 2х2-x-6 квадрат үшмүшесін көбейткіштерге жіктейік. Оның
түбірлері: х1=-1,5; х2=2 болғандықтан, 2х2-x-6=2(х-(-1,5))(х-2)=2(х+1,5)
(х-2)=(2х+3)(х-2) теңдігі орындалады.

1. Есептер шығару:
Деңгейлік тапсырмалар:
А тобы:
№326. Квадрат үшмүшені көбейткіштерге жіктеуңдер: 1) х2-2x-48;
Жауабы: х1=-6; х2=8 болады, көбейткіштерге жіктеу: х2-2x-48=(х+6)(х-8).
2) х2+9x-22;
Жауабы: х1=2; х2=-11 болады, көбейткіштерге жіктеу: х2+9x-22=(х-2)(х+11).

В тобы:
№330. Квадрат үшмүшені көбейткіштерге жіктеуңдер: 1) ах2-(а+с)x+с;
Жауабы: ах2-(а+с)x+с=ах2-аx-xс+с=ах(x-1)-c(x-1)=(ax-c)(x-1).
2) 6х2+5mx+m2;
Жауабы:6х2+5mx+m2=6х2+3mx+2mx+m2=3x(2x+m)+m(2m+m)=(3x+m)(2x+m)

C тобы:
№341. Түбірлері бойынша теңдеулер құрастырып, оларды көпмүше түрінде
жазыңдар. 1) -3;8;
Жауабы:

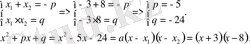
2. Тест сұрақтары
1. ах4+bx2+c=0, мұндағы а≠0 түрінде берілген теңдеу қандай теңдеу?
а)биквадрат теңдеу ә)квадрат теңдеу б)келтірілген
квадрат теңдеу
2. Квадрат теңдеудің неше түрі бар?
а)төрт ә)үш
б)екі
3. 4х2-3x=0 қандай теңдеу?
а)толымсыз квадрат теңдеу; ә) толымды квадрат теңдеу; б)дұрыс жауап жоқ
4. Квадрат теңдеудің қанша түбірі болатынын қалай анықтауға болады?
а)есептің берілуіне байланысты; ә) дискриминантқа б)түбірі жоқ
5. х2-8x+15=0 теңдеуінің түбірлерін Виет теоремасы арқылы жауабын жылдам
тап?
а)2;6 ә)3;6 б)2;6
6. Егер 11 және -2 сандары кез-келген квадрат теңдеудің түбірлері болса,
онда квадрат теңдеуді құрыңдар.
а)х2-10x+25=0 ә)х2-9x-22=0
б)9х2-24x+16=0
7. ах2=0 (мұндағы b=0, с=0). Бұл қандай теңдеудің жазылу түрі?
а)толымсыз ә)келтірілген б)биквадрат
8. 2,1х2+102,3x+0,8=0. Бұл қандай теңдеу, дұрысын анықта?
а)келтірілген ә) толымды б)биквадрат

Тест жауаптары: 1-а, 2-ә, 3-а, 4-ә, 5-ә, 6-ә, 7-а, 8-ә.

ІІІ. Толғаныс.
1. Ребус шешу кезеңі. Жауабы: КВАДРАТ
2. Сөзжұмбақ шешу кезеңі.
1. Квадрат теңдеудің неше түрі бар? (үш)
2. ах2+bx+c=0 түріндегі квадрат теңдеудегі а-қандай коэффициент деп
аталады? (бірінші)
3. b мен c нөлге тең болатын дербес жағдайлардағы квадрат теңдеу қалай
аталады? (толымсыз)
4. Егер рационал теңдеудің екі жақ бөлігінде де бүтін өрнектер жазылса,
онда оны қандай теңдеу деп атаймыз? (бүтін)
5. ах2+bx+c=0 түріндегі квадрат теңдеудегі b-қандай коэффициент деп
аталады? (екінші)
6. Келтірілген квадрат теңдеудің түбірлерінің қосындысы қарама-қарсы
таңбамен алынған екінші коэффициентке, ал көбейтінділері бос мүшеге тең.
Бұл қай теорема? (Виет).

ІV. Қорытындылау, бағалау: Сабаққа жақсы қатысқан оқушыларды кері
байланыс картасымен бағалау. Сабақ бойында жасалған жұмыстарға талдау

V. Үй тапсырмасы: №326, №330.

Бекітемін:
Келісемін:
Мектеп директоры:
ДОІЖО:
________З.Пилалова
__________ Б.Смайлова

C.Торайғыров атындағы жалпы орта мектебі

коммуналдық мемлекеттік мекемесі

А ш ы қ с а б а қ

Сабақтың тақырыбы:

(8 сынып оқушыларымен)

Дайындаған пән мұғалімі: А.Булекбаева

2014-2015 оқу жылы

-----------------------
Толымсыз квадрат теңдеу

Толымды квадрат теңдеу

Квадрат теңдеу түрлері

Келтірілген квадрат теңдеу