Утешов Халел Хайноллаұлы дайындаған аудандық, облыстық және республикалық математикалық олимпиада есептері мен шешімдері (2005-2013)


Дайындаған:

Математика пәнінің жоғары санатты мұғалімі
Утешов Халел Хайноллаұлы
қаңтар 2013 жыл
Аудандық олимпиада
9 сынып . 2005 ж
а, в, с -үшбұрыштың қабырғалары болсын. Үшбұрышқа іштей сызылған шеңбердің центрі О-нүктесі АА 1 биссектрисасын АО:А 1 О=(в+с) :а қатынасында бөлетіндігін
дәлелдеңдер.
Шешуі:
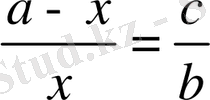 , х=
, х=
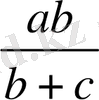 ,
,
BA
1
= a-
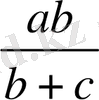 =
=
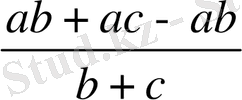 =
=
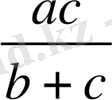 ,
,
AO:A
1
O=c
:
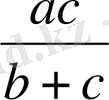 =
=
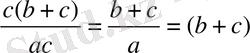 :a
д. к. о
:a
д. к. о
9 сынып. І тур. 2006ж
Үшбұрыштың екі медианасы перпендикуляр орналасқан, m a┴ m b , үшбұрыштың қабырғалары: a, b, c
Дәлелдеу керек: 5с 2 = а 2 +в 2
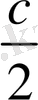
9-сынып. 1-тур . 2008ж
Табаны АД болатын АВСД трапециясы берілген. М нүктесі А және В төбелеріндегі
сыртқы бұрыштарының биссектрисаларының қиылысу нүктесі, ал N нүктесі С және
Д төбелеріндегі сыртқы бұрыштарының биссектрисаларының қиылысу нүктесі.
МN кесіндісі трапеция периметрінің жартысына тең екендігін дәлелдеңдер.
Дәлелдеу керек
MN=
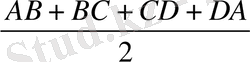
P=
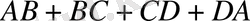
Шешуі: ∆АВМ -тік бұрышты үшбұрыш, себебі ішкі тұстас бұрыштардың биссектрисалары тік бұрыш жасап қиылысады.
Тікбұрышты үшбұрыштың тікбұрышының медианасы гипотенузаның жартысына тең.
ME=
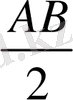 сол сияқты FN=
сол сияқты FN=
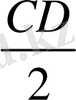 EF=
EF=
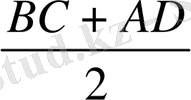
ME+EF+FN=
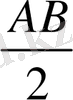 +
+
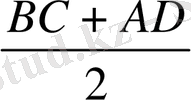 +
+
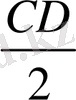 =
=
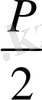
9 сынып. ІІ тур . 2008ж
Берілгені: а, в, с - үшбұрыштың қабырғалары және
а+в+с =2
Дәлелдеу керек : а 2 +в 2 +с 2 <2(2- авс ) екендігін.
Дәлелдеу жолы:
а, в, с- үшбұрыштың қабырғалары болғандықтан, мына теңсіздіктер тура болады:
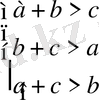 бағандап көбейтуге болады, өйткені
а>0 в>0
с>0
бағандап көбейтуге болады, өйткені
а>0 в>0
с>0
(а+в) (в+с) (а+с) >авс
(ав+ас+в 2 +вс) (а+с) =а 2 в+а 2 с+ав 2 +авс+авс+ас 2 +в 2 с+вс 2 >авс
ав(а+в+с) +ас(а+в+с) +вс(в+с-а) >0
в+с=2-а болғандықтан 2ав+2ас+вс(2-а-а) >0
2ав+2ас+вс(2-2а) >0
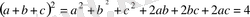 бұдан 2ав+2вс+2ас=4-
бұдан 2ав+2вс+2ас=4-
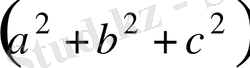 4-(а
2
+в
2
+с
2
) >2авс 4-2авс>а
2
+в
2
+с
2
2(2-авс) > а
2
+в
2
+с
2
д. к. о
4-(а
2
+в
2
+с
2
) >2авс 4-2авс>а
2
+в
2
+с
2
2(2-авс) > а
2
+в
2
+с
2
д. к. о
9 сынып. ІІ тур. 2007ж
Берілгені: кез-келген а, в, с -теріс емес сандар үшін келесі теңсіздікті дәлелдеңдер:
ав+вс+ас
≥
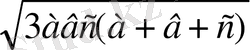
Шешуі: Теңсіздіктің екі жағын авс -ға бөлуге болады, себебі берілгені бойынша а, в, с - оң сандар.
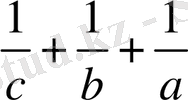 ≥
≥
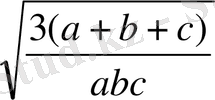
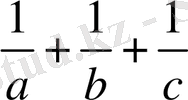 ≥
≥
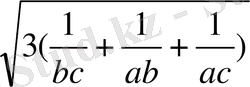 теңсіздіктің екі жағын квадраттаймыз, сонда теңсіздік мынадай түрге келеді:
теңсіздіктің екі жағын квадраттаймыз, сонда теңсіздік мынадай түрге келеді:
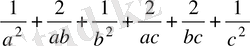 ≥
≥
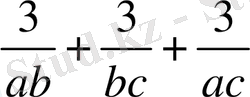
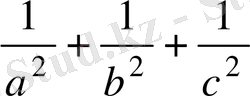 ≥
≥
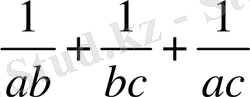 теңсіздіктің екі жағын 2-ге көбейтіп, айырманың квадратына келтіреміз.
теңсіздіктің екі жағын 2-ге көбейтіп, айырманың квадратына келтіреміз.
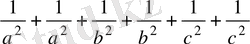 ≥
≥
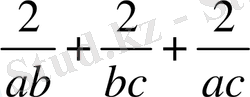
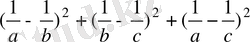 ≥0 д. к. о.
≥0 д. к. о.
9 сынып. ІІ тур . 2006ж
Диаметрі d-ға тең дөңгелекте өзара перпендикуляр АВ және CD хордалары жүргізілген. AC 2 +BD 2 =d 2
болатынын дәлелдеу керек.
Шешуі:
AD
2
=AE
2
+ED
2
S
ABD
=
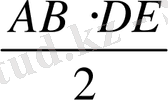 S
ABD
=
S
ABD
=
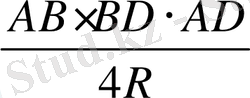
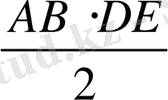 =
=
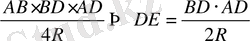
S
ACD
=
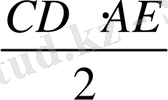 S
ACD
=
S
ACD
=
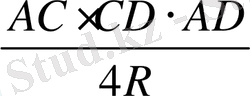
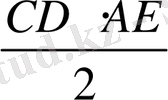 =
=
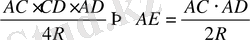
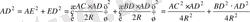
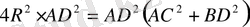
Бұдан
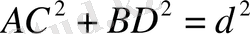 шығады
.
шығады
.
Есептеңдер:
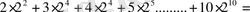
Шешуі: Қосылғыштарды бағандап жазамыз, сонда әрбір жол геометриялық прогрессияның қосындысы болады.
2 2 +2 3 +2 4 +2 5 +2 6 +2 7 +2 8 +2 9 +2 10
2 2 +2 3 +2 4 +2 5 +2 6 +2 7 +2 8 +2 9 +2 10
2 3 + . . . +2 10
2 4 + . . . +2 10
. . .
. . .
2 9 +2 10
2 10
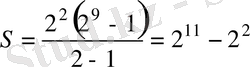
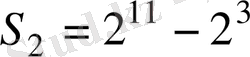
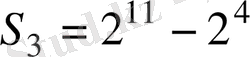 т. с. с.
т. с. с.
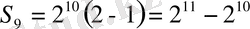 Бәрін қосамыз, сонда
Бәрін қосамыз, сонда
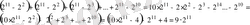 Жауабы:
Жауабы:
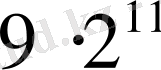
10 сынып. 1 тур . 2006ж
Берілген
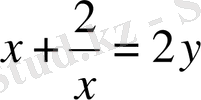
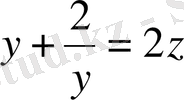
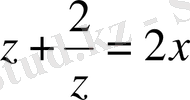 теңдіктерін қанағаттандыратын барлық x, y, z нақты сандарын тап.
теңдіктерін қанағаттандыратын барлық x, y, z нақты сандарын тап.
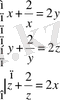
Жүйедегі теңдіктерді бағандап қосамыз, сонда
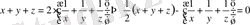
Жүйенің теңдіктерін 2-ге бөлеміз, сосын квадраттаймыз, айырманың квадратына келтіреміз де түбірін табамыз.
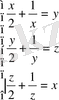
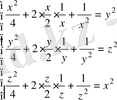
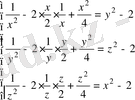
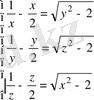
Жүйенің теңдіктерін бағандап қосайық
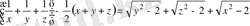
Теңдіктің сол жағы нөлге тең, олай болса оң жағы да нөлге тең болады
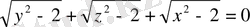 бұл теңдік орындалуы үшін
бұл теңдік орындалуы үшін
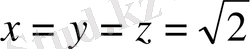 шарты орындалуы қажет.
шарты орындалуы қажет.
10 сынып. ІІ тур. 2008ж
АВС үшбұрышында
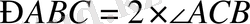 теңдігі орындалады.
теңдігі орындалады.
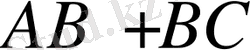 <
<
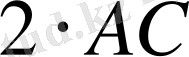 екендігін дәлелдеңдер.
екендігін дәлелдеңдер.
Биссектрисаның қасиеті бойынша
DC
табамыз:
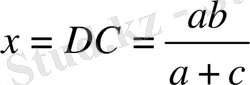
∆ BDC- тең бүйірлі, өйткені
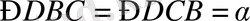
Үшбұрыштың қабырғаларының теңсіздігі бойынша:
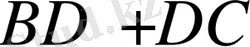 >
а
>
а
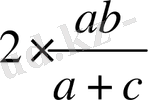 >
а
2ав>
>
а
2ав>
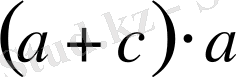
2
в
>
а+с
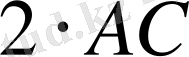 >
>
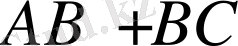 д. к. о.
д. к. о.
11 сынып. І тур. 2007ж
Нақты х және у сандары келесі шарттарды қанағаттандырады:
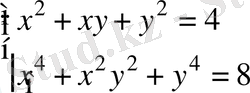 Онда
Онда
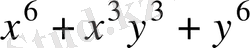 натурал сан екенін дәлелдеңіз және оны табыңыз.
натурал сан екенін дәлелдеңіз және оны табыңыз.
Шешуі
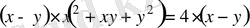
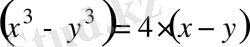
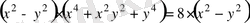
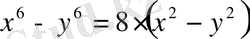
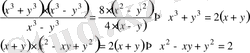
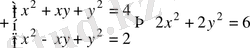
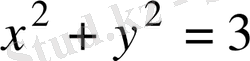
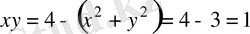
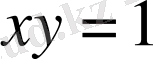
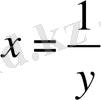
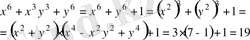
Сонымен,
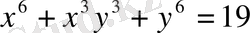 д. к. о.
д. к. о.
11 сынып. ІІ тур . 2007ж
Қай сан үлкен?
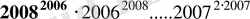
Шешуі: 2007=a деп алсақ,
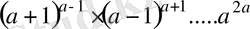
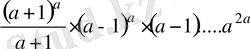
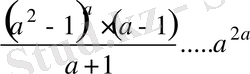
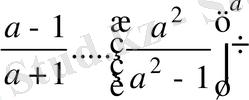
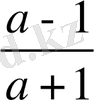 <1 және
<1 және
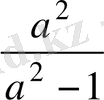 Equation. 3 >1
Equation. 3 >1
Сонымен,
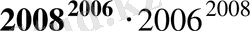 <
<
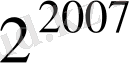 д. к. о.
д. к. о.
10 сынып. ІІ тур 2007ж
1-ден 127-ге дейінгі натурал сандарды топтағы сандардың қосындылары өзара тең бірнеше (бірден артық) топқа бөлген. Осындай топтардың саны жұп болатынын дәлелде.
Шешуі: Тақ сандар мен жұп сандар тізбегін айырып аламыз, екеуі де арифметикалық прогрессия болады.
1+3+5+ . . . +125+127=S т
2+4+6+ . . . +124+126=S ж
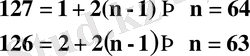 қосындысын табамыз:
қосындысын табамыз:
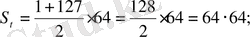
S
ж
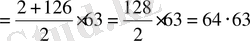
Сонымен, екі сандар тобы пайда болды. Тақ сандардың қосындысы жұп сандардың қосындысынан 64-ке артық, екі қосындыны теңестіру үшін 32 санын жұп сандарға қосу қажет. Сонда екі топтың қосындысы теңеседі:
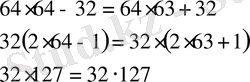
Өзара тең екі топтан өзара тең бірнеше топтар құрастыруға болады, олардың саны жұп болады.
9 сынып. І тур. 2008ж
Дәлелдеңдер:
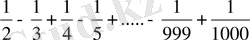 <
<
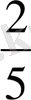
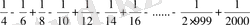 <
<

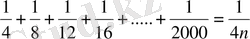
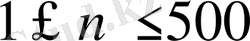
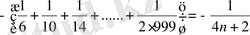
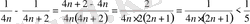
 болғанда
болғанда
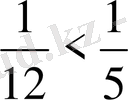
11 сынып.
Теңдеулер жүйесін шешіңдер.
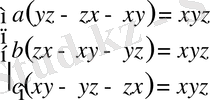 xyz≠0 болсын, жүйенің теңдеулерін xyz-ке бөліп мынадай жүйе аламыз:
xyz≠0 болсын, жүйенің теңдеулерін xyz-ке бөліп мынадай жүйе аламыз:
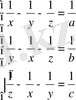 бағандап қоссақ мынау шығады:
бағандап қоссақ мынау шығады:
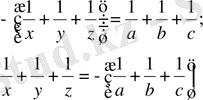
Шыққан теңдеуді (1) жүйенің әрбір теңдеуімен қоссақ мынадай жүйе аламыз:
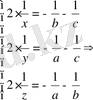
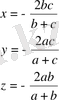
9 класс ІІ тур 2007ж
1) Офисте жұмыс істейтін 94 қызметкердің әрбіреуі әлде қазақша, әлде орысша біледі. Қазақша сөйлейтіндердің 70%-і орысша біледі, ал орысша сөйлейтіндердің 80%-і қазақша біледі. Офисте қанша қызметкер екі тілде сөйлейді?
Шешуі:
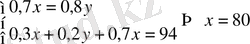
80 қызметкер қазақ тілін біледі, 80∙0, 7=56 қызметкер екі тілде сөйлейді.
10-сынып 2-тур 2007ж
2) Иесі кодты дипломатты ашатын үш цифрды ұмытып қалды, (000-999) . Бірақ ол үш цифрдың қосындысы 15-ке тең екендігін біледі. Дипломатты ашу мүмкіндігінің ең аз саны қанша?
Шешуі:
Дипломатты ашу мүмкіндігінің ең аз саны: 73
АВС үшбұрышының АР биссектриссасы жүргізілген. BP=16 PC=20 ABP үшбұрышына сырттай сызылған шеңбердің центрі АС қабырғасында жатыр. АВ-ны тап.
AB=x деп алайық, сонда
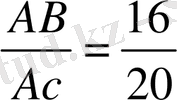
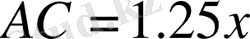

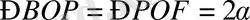 (центрлік бұрыштар)
(центрлік бұрыштар)

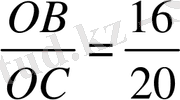
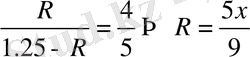
Қиюшылардың қасиетін қолданамыз:
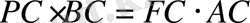
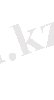

9 - сынып І тур 2010 жыл
Өрнекті ықшамдаңдар:

10-сынып 2009ж
Теңсіздікті дәлелдеңдер
:
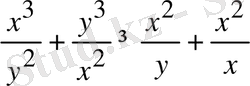 (х, у>0)
(х, у>0)
Екі жағын квадраттаймыз, сонда
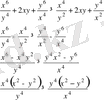
Сол жаққа жинап ортақ бөлімге келтіреміз, сонда
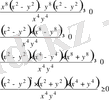
д. к. о.
Алматы қаласындағы Жәутіков конкурсы. 2009ж
АВСД трапециясының диагоналдары О нүктесінде АО:ОС=3:1 қатынасында қиылысады және АОД үшбұрышының ауданы 36-ға тең. Трапецияның ауданын табыңыз.
А) 81 В) 108 С) 96 Д) 58 Е) 64
Шешуі:
 S
∆AOD
=36
S
∆AOD
=36
S
MBCA
=S
BCED
=1z∙h S
∆CDE
=
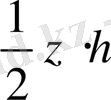
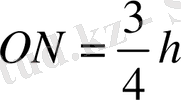
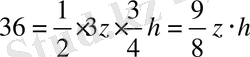
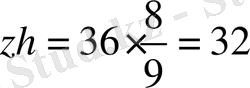 S
BCD
=16 S
ABC
=16
S
BCD
=16 S
ABC
=16
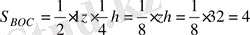
Сонымен S тр =36+16+16-4=64. ∆AOD~∆BOC
9-сынып 2010 жыл
а+в+с=х+у+z теңдігін қанағаттандыратын теріс емес а, в, с және оң х, у, z нақты сандары үшін теңсіздікті дәлелдеңдер:
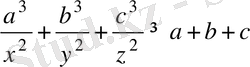
Шешуі:
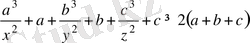 теңсіздіктің сол жағына Коши теңсіздігін қолданамыз, сонда
теңсіздіктің сол жағына Коши теңсіздігін қолданамыз, сонда
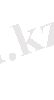
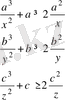

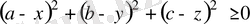
8-сынып 2009ж
Сүйір бұрышты АВС үшбұрышының АВ және АС қабырғаларының орталарын сәйкесінше М және N
деп белгілейік. Олай болса, ВС қабырғасынан алынған кез-келген S нүктесі үшін
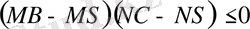 болатынын
болатынын
дәлелдеңдер.
Егер S нүктесі ВС қабырғасының ортасы болса,

Егер S
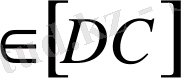 болса, <МДВ< <МДS, сондықтан МВ<МS
болса, <МДВ< <МДS, сондықтан МВ<МS
МВ-МS<0 <NCS< <NSC болғандықтан NS<NC
NC-NS>0
Егер S
 болса, керісінше болады.
болса, керісінше болады.
10-сынып 2-тур 2011 ж
Қосындысы 2-ге тең оң нақты х, у, z сандары үшін
теңсіздікті дәлелдеңдер:
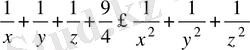
Шешуі: Теңсіздіктің екі жағын 2-ге көбейтеміз, сонда
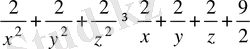
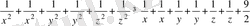
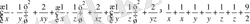

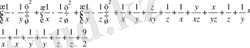
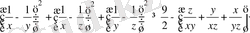
Теңсіздіктің оң жағының теріс екендігін дәлелдесек
жеткілікті.
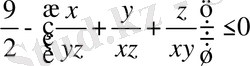 немесе
немесе
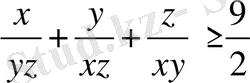
Теңсіздікті 2-ге көбейтіп, сол жағына Коши теңсіздігін
қолданамыз:
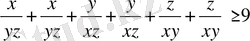
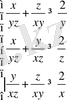 бұдан шығады:
бұдан шығады:
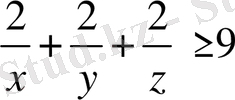
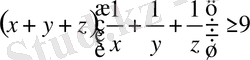 жақшаларды ашайық, сонда
жақшаларды ашайық, сонда
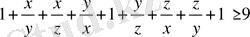
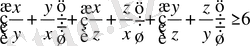
д. к. о
11-сынып 2011 жыл
Қосындысы 1-ге тең оң нақты a, b, c сандары үшін
теңсіздікті дәлелдеңдер:
abc≤(ab+bc+ca) (a 2 +b 2 +c 2 ) 2
Шешуі: Кез-келген оң нақты а, в, с сандары үшін мына теңсіздік тура екендігін білеміз:
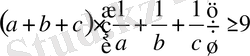 а+в+с=1 болғандықтан,
а+в+с=1 болғандықтан,
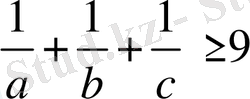
Берілген теңсіздікті (авс) -ға бөлуге болады:
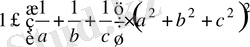 ,
,
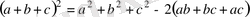
бұдан
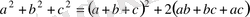
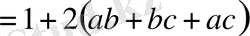
Сонда
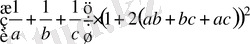
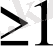 теңсіздігі тура,
теңсіздігі тура,
өйткені бірінші қосылғыш 9-дан кем емес, екінші
қосылғыш 1-ден артық. д. к. о.
9-сынып 2011 жыл
АВСД квадратының сыртынан АР=АВ және
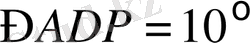
болатындай етіп Р нүктесі алынған.
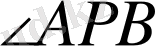 бұрышының
бұрышының
мүмкін ( градустық) мәндерін анықтаңдар.
10-сынып. 2011 ж
Кез-келген натурал n>1 және k>1 сандары үшін
n k+2 -n k саны 12-ге қалдықсыз бөлінетінін дәлелдеңдер.
9-сынып 2010 ж
m натурал саны үшін 8 m санының ондық жазбасындағы
цифрлардың қосындысы 8-ге тең екені белгілі.
Осы 8 m санының соңғы цифры 6-ға тең болуы мүмкін
бе?
10-сынып 2010 ж
АВСД параллелограмының
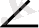 В бұрышы доғал. АД
В бұрышы доғал. АД
түзуі АВС үшбұрышына сырттай сызылған
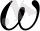 шеңберін
шеңберін
Е≠А нүктесінде қияды, ал СД түзуі
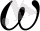 шеңберін F≠C
шеңберін F≠C
нүктесінде қияды. Онда DEF үшбұрышына сырттай
сызылған шеңбердің центрі
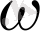 -да жататынын дәлелдең-
-да жататынын дәлелдең-
дер.
11-сынып 2011 ж
CK және BL биіктіктері үшін AB+CK=AC+BL теңдігі
орындалатын барлық АВС үшбұрыштарын сипаттаңдар.
Мұғалімдердің облыстық олимпиадасы
желтоқсан-2011
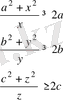
- а, в, с >0 үшін>2 теңсіздігін
дәлелдеңдер.
- Кез-келген натурал n үшін мына теңсіздікті
математикалық индукция әдісімен дәлелдеңдер:
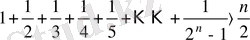
- +қосындысы 7-ге бөлінетінін
дәлелдеңдер.
- Төбелері (0; 0), (1; 0), (1; 1) және (0; 1) нүктелерінде
болатын квадратқа кездейсоқ М(х, у) нүктесі
тасталады. С={(х, у) : х 2 +у 2 ≤а 2 , а>0} оқиғасының
ықтималдығын табу керек.
- SАВСД тіктөртбұрышты пирамиданың табаны
АВСД, барлық бүйір жақтарының аудандары
тең.
жазықтығы оның SA, SB, SC, SD бүйір
қырларын сәйкесінше А 1 , В 1 , С 1 , Д 1 нүктелерінде
қияды және SA 1 B 1 C 1 D 1 пирамидасының
көршілес екі бүйір жағының аудандары тең болады. Осы пирамиданың қалған екі бүйір
жақтарының аудандарының тең болатынын
дәлелдеңдер.
- Жазықтықта қызыл, көк және жасыл түсті
15 әртүрлі нүктелер алынған. Басқа түсті нүкте-
лер жоқ. Қызыл және көк түсті нүктелердің
барлық парларының ара қашықтығы 51, дәл
осылайша қызыл және жасыл нүктелердің ара
қашықтығы 39, ал көк және жасыл нүктелердің
ара қашықтығы 1. Жазықтықта қанша қызыл,
көк, жасыл нүктелер алынған?
(Мүмкін жағдайлардың барлығы қарастырылуы керек) .
Құрметті әріптестер!
Облыстық олимпиада есептерінің шешу жолдарын интернетке жіберулеріңізді сұраймын.
Сәлеммен Халел Хайноллаұлы
Зеленов ауданы Батыс қазақстан облысы
2012 жылғы оқушылардың Республикалық математикалық олимпиадасының тапсырмалары
Жұмыс уақыты-4 сағат
Әр есеп 7 ұпайға бағаланады.
9-сынып 2-тур
- Қаржы министрі мемелекетте айналысқа тек қана
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz