Иррационал теңдеулерді шешу әдістері және бөгде түбірлерді анықтау

Скачать

Алгебра және анализ бастамалары

Сабақтың тақырыбы : Иррационал теңдеулерді шешу

Сабақтың мақсаты : 1. Оқушыларға иррационал теңдеулер туралы түсіндіру .

2. Иррационал теңдеулерді шешу тәсілдерін үйрету .

3. Бөгде түбірлерді анықтау тәсілін үйрету .

Дамытушылығы : Оқушылардың ойлау қабілеттерін арттыруға ықпал жасау

және де өз бетінше шығармашылықпен жұмыс жасау

дағдыларын қалыптастыруға ықпал ету .

Тәрбиелік мәні : Оқушылар бойында азаматтық қасиеттерді қалыптастыру .

Сабақтың көрнекілігі: Формулалар жазылған көрнекі кестелер . Интерактивтік

тақтадағы слайдтар .

Сабақтың түрі : Дәстүрлі сабақ

1. Сұрақ -жауап
2. Баяндау
3. Білімді бекіту

Сабақтың барысы : І Ұйымдастыру кезеңі

Оқушылардың сабаққа қатысуын тексеріп, психологиялық

дайындығын қалыптастырамын.

ІІ Үй тапсырмасын тексеру

ІІІ Негізгі бөлім

Жаңа тақырыпты түсіндіру үшін алдымен өтілген тақырыптармен байланыстыру жағын қарастырамын .

Ол үшін оқушылардан мына төмендегі сұрақтарға жауап алуға әрекет етемін .

1. Нақты санның n ші дәрежелі түбір дегеніміз не ?

А санының n -ші дәрежелі түбірі деп n-ші дәрежесі а санына тең болатын в санын айтады . 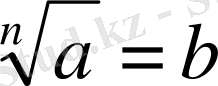; мұндағы

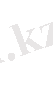
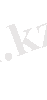
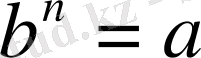
2. n-ші дәрежелі түбірдің қасиеттерін ата.

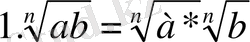
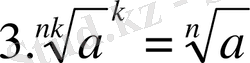Equation. 3 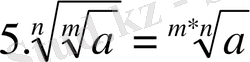Equation. 3

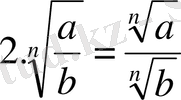
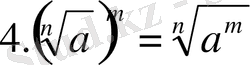Equation. 3

3. Рационал сандар дегеніміз не

Бүтін, бөлшек натурал сандар қиынынан құралған сандарды айтамыз .

4. Иррационал сан дегеніміз не

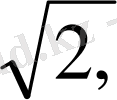
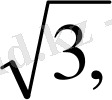
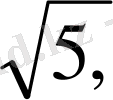
Мысалы, 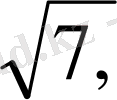т. с. с

5. Иррационал теңдеу деп

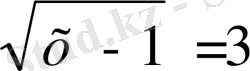
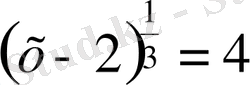
6. Иррационал теңдеулерді шешу тәсілдері

А) Дәрежеге шығару әдісі.

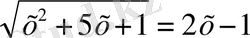
Ә) Жаңа айнымалы енгізу әдісі.

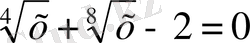
Б) Бөгде түбірді анықтау.

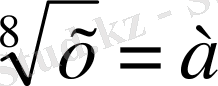
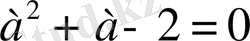түріне келтіру

ІІ ЕСЕПТЕР ШЫҒАРУ

1. Өтілген жаңа тақырып түсінікті болу үшін мына төмендегі есептерді оқулық бойынша жазу тақтасына көрсетемін

А - деңгейі бойынша № 120 (1), № 121 (1), № 122 (1)

В - деңгейі бойынша №122 (1), № 123 (1),

№ 124(1), №126(1)

тапсырмаларды көрсетемін.

А. № 120 1)

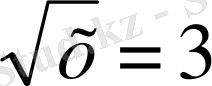
Х = 9

Шығару тәсілі - дәрежеге шғару тәсілі

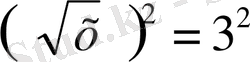тексереміз

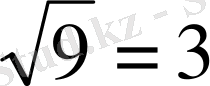
Х = 9

№ 121 1) 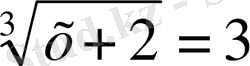Тексереміз

Х + 2 = 27

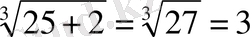
Х = 25

№122 1)

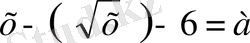
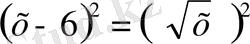
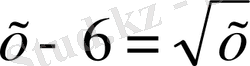х ² -12х + 36 = х

Х ₁ = 3 х ₂ = 9

Тексеру арқылы бөгде түбірді анықтаймыз. Жауабы: х = 9

№ 123 1)

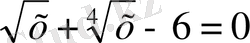
Жаңа айнымалы енгізу арқылы шешеміз 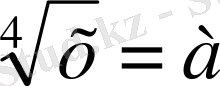деп алсақ, сонда теңдеу мына түрге келеді а ² + а - 6 = 0

а ₁ = - 3: а ₂ =2

а - ның табылған мәндерін бастапқы түрлендірген орынға қойсақ,

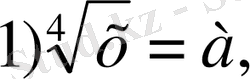
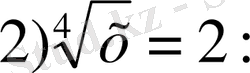тексерсек,

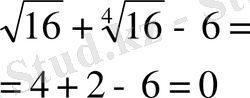
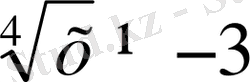
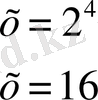Жауабы x= 16

В) №125 1) < = >

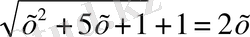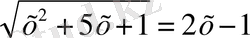
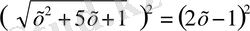
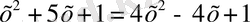
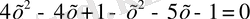
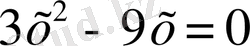
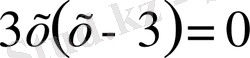
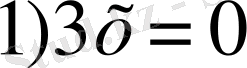
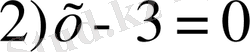
Тексереміз 1) X=0

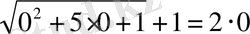
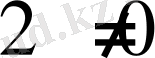
2) X=3

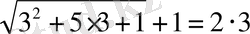
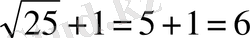
6 = 6

Жауабы x= 3

Сайыс кезеңі

1 . Оқушыларға осы көрсетілген есептердің қалған бөліктерін шығарту барысында, өтілген тақырыпты қандай деңгейде меңгергендіктерін байқау үшін «Кім жылдам» атты жарыс сабағын ұйымдастырамын.

Сонымен қатар, оқушылардан шығару тәсілі туралы да сұрап білуге әрекет етемін.

2. Сабақты қорытындылау.

3. Оқушылар білімін бағалау.

4. Үйге тапсырма: 123, (б)

124 (в)

125 (в)

шығарып келу

• Іс жүргізу
• Автоматтандыру, Техника
• Алғашқы әскери дайындық
• Астрономия
• Ауыл шаруашылығы
• Банк ісі
• Бизнесті бағалау
• Биология
• Бухгалтерлік іс
• Валеология
• Ветеринария
• География
• Геология, Геофизика, Геодезия
• Дін
• Ет, сүт, шарап өнімдері
• Жалпы тарих
• Жер кадастрі, Жылжымайтын мүлік
• Журналистика
• Информатика
• Кеден ісі
• Маркетинг
• Математика, Геометрия
• Медицина
• Мемлекеттік басқару
• Менеджмент
• Мұнай, Газ
• Мұрағат ісі
• Мәдениеттану
• ОБЖ (Основы безопасности жизнедеятельности)
• Педагогика
• Полиграфия
• Психология
• Салық
• Саясаттану
• Сақтандыру
• Сертификаттау, стандарттау
• Социология, Демография
• Спорт
• Статистика
• Тілтану, Филология
• Тарихи тұлғалар
• Тау-кен ісі
• Транспорт
• Туризм
• Физика
• Философия
• Халықаралық қатынастар
• Химия
• Экология, Қоршаған ортаны қорғау
• Экономика
• Экономикалық география
• Электротехника
• Қазақстан тарихы
• Қаржы
• Құрылыс
• Құқық, Криминалистика
• Әдебиет
• Өнер, музыка
• Өнеркәсіп, Өндіріс