Арифметикалық және геометриялық прогрессиялар: сабақ жоспары, теория және практикалық есептер


Батыс Қазақстан облысы
Жәнібек ауданы, Жақсыбай ауылы
М. Б. Ықсанов атындағы орта жалпы
білім беретін мектеп- балабақша
Зубайров Алмабек Жасталапұлы
Математика пәнінің мұғалімі
Сабақтың тақырыбы: Арифметикалық және геометриялық прогрессия
Сабақтың мақсаты:
1. Білімділік:
Арифметикалық, геометриялық прогрессиялардың қасиеттерін, ерекшеліктері мен ұқсастықтарын, формулаларын сатылай, жүйелі, комплексті меңгерту. Есептер шығаруда дұрыс қолдана алуға үйрету.
2. Дамытушылық:
Оқушылардың ойлау, есте сақтау, елестету қабілеттерін, танымын дамыту.
3. Тәрбиелілік:
Оқушылардың белсенділігін арттыру, өз бетінше оқуға, ізденуге тәрбиелеу.
Сабақтың түрі: Қорытындылау сабағы
Сабақтың әдісі: Сатылай комплексті талдау технологиясын, сұрақ-жауап, есептерді шығару, тест алуда деңгейлеп оқыту технологиясын қолдану.
Сабақтың көрнекілігі: плакаттар, тест карточкалары, бағалау беттері
Сабақтың барысы: І. Ұйымдастыру кезеңі
ІІ. Негізгі бөлім

- Анықтамасы
2. Тану
Арифметикалық прогрессия Геометриялық прогрессия
2. 1. а 1 , а 2 , а 3 , . . . , а n
Мысалы
1, 4, 7, . . .
а 2 - а 1 = а 3 - а 2 = …= a n-1 - a n =d
2. 2. (a n ) - арифметикалық
прогрессия
а 1 - бірінші мүше
d - айырымы
n - мүшелерінің саны
а n - n-ші мүшесі
S n - алғашқы n мүшесінің
қосындысы
b 1 , b 2 , b 3 , . . . , b n
Мысалы
2, 4, 8, 16 . . .
b 2 : b 1 = b 3 : b 2 = …= b n+1 : b n =q
(b n ) - геометриялық
прогрессия
b 1 - бірінші мүше
q - еселік
n - мүшелерінің саны
b n - n-ші мүшесі
S n - алғашқы n мүшесінің
қосындысы
2. 3. Арифметикалық және геометриялық прогрессиялар -
тізбектер. Тізбектер бірнеше тәсілдермен берілетінін еске түсіре кетейік:
2. 4. Математикалық белгі
Арифметикалық Геометриялық
прогрессия прогрессия
3. Қасиеті

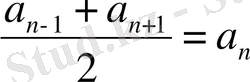
Мысалы
1, 3, 5, 7, . . .
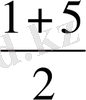
= 3;
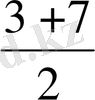
= 5
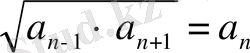
Мысалы
2, 2 2 , 2 3 , 2 4 , . . .
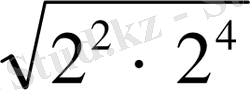
= 2 2
= 2 3
4. Маңызды түйін
4. 1. Рекурренттік формуласы
a
n+1
= a
n
+ d, n
 Equation. 3 N b
n+1
= b
n
Equation. 3 N b
n+1
= b
n
 Equation. 3 q, n
Equation. 3 q, n
 N
N
4. 2. Қабылдай алатын мәндері
a
1
 d -
d -
 сандар b
1
сандар b
1
 0, q
0, q
 0
0
d - айырымы q - еселігі
4. 3. Жалпы мүшесінің формуласы
a
n
= a
1
+ (n-1) d b
n
= b
1
 Equation. 3 q
n-1
Equation. 3 q
n-1
Айырымын табу: Еселікті табу:
d = a
n+1
- a
n
q =
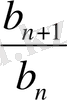
4. 4. Алғашқы n мүшесінің қосындысының формуласы
S
n
=
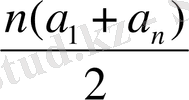 S
n
=
S
n
=
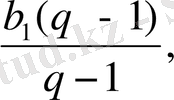 (q
(q
 1)
1)
4. 5. Шексіз кемімелі
геометриялық
прогрессияның
қосындысы
S =
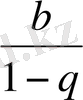 Equation. 3 ;
Equation. 3 ;
 < 1
< 1
5. Түрге айыру
5. 1. Арифметикалық прогрессия
d>0, өспелі
айырымы арифметикалық прогрессия
d<0, кемімелі
5. 2. Мүшелері тұрақты бір ғана сан болатын тізбек тұрақты
геометриялық прогрессия деп аталады.
Мысалы: 4, 4, 4, . . . тізбегі q = 1 болғанда тұрақты
геометриялық прогрессия болады.
6. Түрлену
Арифметикалық прогрессия Геометриялық прогрессия
6. 1.
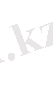
Equation. 3 мүшесін табу
a 1 = 2 b 1 = 3
d = 5 q = 2
a 7 - ? b 5 - ?
а
7
=a
1
+6d=2+30=32 b
5
=b
1
 q
4
=3
q
4
=3
 2
4
=3
2
4
=3
 16=48
16=48
6. 2. Айырымын табу 6. 3. Еселігін табу
a 1 =5 b 1 = 3
a 2 =7 b 2 = 9
d - ? q - ?
a
2
= a
1
+ d b
2
= b
1
 q
q
d = a
2
-a
1
q =
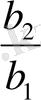 =
=
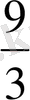 = 3
= 3
d = 2 q = 3
6. 4.
мүшелерінің қосындысын есептеу
a 1 = 9 b 1 = 1
a
2
= 13 q =
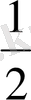
S 5 - ? S 4 - ?
d = a
2
- a
1
= 13 - 9 = 4 b
4
= b
1
 q
3
= 1
q
3
= 1
 (
(
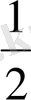 )
3
=
)
3
=

a 5 = a 1 +4d = 9+16=25
S
5
=
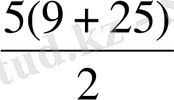 =
=
 = 85 S
4
=
= 85 S
4
=
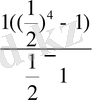 =
=
 = =
= =
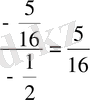
 2 =
2 =
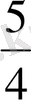 =1
=1
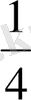
3. Есептер шығару
№1. Арифметикалық прогрессияның бірінші мүшесі 5-ке тең, айырымы
7-ге тең, оның он екінші мүшесі неге тең екенін бізден сұрайды.
Берілгені: а 1 =5
d=7
a 12 =?
Шешуі:
a
12
= a
1
+ 11d=5+11
 7=82
7=82
Жауабы: 82
№3. Арифметикалық прогрессияның бірінші мүшесі 25-ке, айырымы 4-ке тең, оның алғашқы он мүщесінің осындысын табыңдар.
Берілгені: a 1 = 25
d=4
S 10 - ?
Шешуі:
a
10
= a
1
+ 9d=25+9
 4=61
4=61
S
10
=
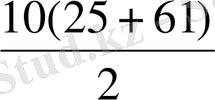 = 5
= 5
 86 = 430
86 = 430
Жауабы: 430
№5. Берілгені: a 10 = 120
d = 12
a 1 - ?
Шешуі:
a 10 = a 1 + 9d
a 1 =a 10 -9d=120-108=12
a 1 =12
Жауабы: 12
№2.
Геометриялық прогрессияның бірінші мүшесі 3-ке, еселігі
 - ге тең, оның үшінші мүшесі неге тең екені бізден сұрайды.
- ге тең, оның үшінші мүшесі неге тең екені бізден сұрайды.
Берілгені: b 1 =3
q=
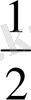
b 3 =?
Шешуі:
b
3
= b
1
 q
2
=3
q
2
=3

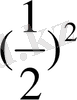 = 3
= 3

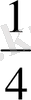 =
=
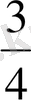
Жауабы:
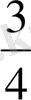
№4. Геометриялық прогрессияның бірінші мүшесі мен үшінші мүшесінің қосындысы 60-қа тең, еселігі 3-ке тең. Оның алғашқы төрт мүшесінің қосындысын табыңдар.
Берілгені: b 1 +b 3 = 60
q = 3
S 4 - ?
Шешуі:
b
3
= b
1
 q
2
q
2
b 1 + b 1 q 2 = 60
b 1 (1+q 2 ) = 60
b 1 (1+9) = 60
10b 1 =60
b 1 =6
S
4
=
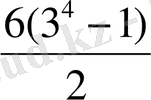 = 3
= 3
 80 = 240
80 = 240
Жауабы: 240
№6. Берілгені: b 1 =5
b 5 =3125
q - ?
Шешуі:
b 5 =b 1 q 4 ;
q
4
=
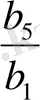 =
=
 =625
=625
q 4 = 625
q 4 = 5 4
q = 5
Жауабы: q = 5
4. Деңгейлік тапсырмалар бойынша тест алу
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz