Шеңбер ұзындығы мен π саны: есептер шығару сабағы

Тақырыбы: Шеңбердің ұзындығы, π саны тақырыбына есептер шығару.

Мақсаты: 1. Шеңбердің ұзындығы, π саны тақырыбы бойынша алған теориялық мағлұматтарын қайталау, есеп шығаруда орынды қолдана білуге үйрету.

2. Есеп шығаруда нәтижелерді қорытындылай білуге, ойын толық жеткізе білуге, есептерді ауызша шығаруға баулу.

3. Ізденуге, тиянақтылыққа, жолдастыққа, еңбекке баулу.

Әдісі: сұрақ-жауап, практика-тәжірибе

Түрі: аралас

Көрнекілігі: мультимедиа, тәжірибеге керекті екі түсті жіп, қайшы.

Сабақ жоспары: I. Ұйымдастыру кезеңі.

II. Ой қозғау - үй тапсырмасын тексеру.

III. Ой толғау - өткенді қайталау.

IV. Ой түйін - кітаппен жұмыс

V. Ой сергіту - шығармашылықты шыңдау

VI. Ой бөлісу - ауызша есептер (қорытындылау) .

Үйге тапсырма беру

Бағалау

Сабақ жүрісі: 1. ұйымдастыру кезеңі (оқушылармен амандасып, қатыстарын және сабаққа дайындықтарын тексеру) .

2. Ой қозғау - үй тапсырмасын тексеру .

№ 213 есеп (ауызша тексеріледі)

1) Бер: α=30 ⁰ Шешуі:

т/к: n n= $\frac{360^{0}}{30^{0}}$ $\frac{360^{0}}{30^{0}}$ = 12 (қабырға саны)

2) Бер: α=4 ⁰ Шешуі:

т/к: n n= $\frac{360^{0}}{4^{0}}$ $\frac{360^{0}}{4^{0}}$ = 90 (қабырға саны)

№ 215 (тақтада тексеріледі) Шешуі:

Бер: n=5; а=3см $R = \ \frac{а}{2\sin\frac{180^{0}}{5}}$ $R = \ \frac{а}{2\sin\frac{180^{0}}{5}}$ = $\frac{3}{2\sin 36^{0}} \approx 2, 6см;$ $\frac{3}{2\sin 36^{0}} \approx 2, 6см;$

т/к: r; R r= $\frac{а}{2{tg}\frac{180^{0}}{5}}$ $\frac{а}{2{tg}\frac{180^{0}}{5}}$ = $\frac{3}{2{tg}36^{0}} \approx 2, 1см;$ $\frac{3}{2{tg}36^{0}} \approx 2, 1см;$

Жауабы: $\approx 2, 6см; \ \approx 2, 1см;$ $\approx 2, 6см; \ \approx 2, 1см;$

3. Ой толғау - өткенді қайталау.

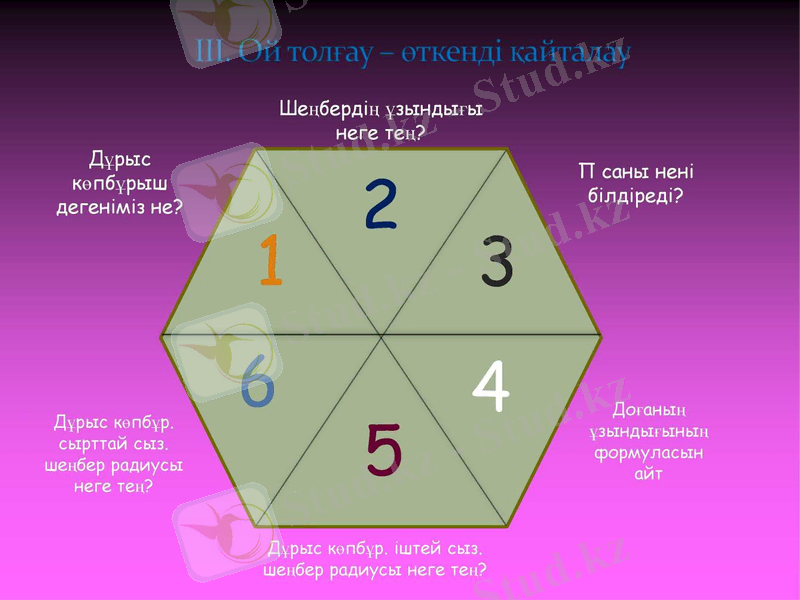
Мультимедиадағы мына дұрыс көпбұрыш сипатталады (мына сұрақтар қандай көпбұрышқа жазылған? Анықтамасы, элементтері айтылады. )

4. Ой түйін - кітаппен жұмыс

№217 (тақтада 1 оқушы шығарады)

Бер: d= 18м; n= 10 Шешуі:

т/к: а ₁ , а ₂ $R = \ \frac{а}{2\sin\frac{180^{0}}{\text{n}}}$ $R = \ \frac{а}{2\sin\frac{180^{0}}{\text{n}}}$ ; а ₁ = 2R $\sin\frac{180^{0}}{\text{10}}$ $\sin\frac{180^{0}}{\text{10}}$ = $d\sin 18^{0} \approx 5, 6м;$ $d\sin 18^{0} \approx 5, 6м;$

r= $\frac{а}{2{tg}\frac{180^{0}}{n}};$ $\frac{а}{2{tg}\frac{180^{0}}{n}};$ а ₂ = 2r ${tg}\frac{180^{0}}{10} = \ d{tg18}^{0} \approx 5, 8м;$ ${tg}\frac{180^{0}}{10} = \ d{tg18}^{0} \approx 5, 8м;$

Жауабы: $\approx 5, 6м; \ \approx 5, 8м$ $\approx 5, 6м; \ \approx 5, 8м$

№220 (тақтада орындалады) Шешуі:

Бер: Дұрыс көпбұрыш; АВ= $\ \frac{а}{2};$ $\ \frac{а}{2};$ М К

а - қабырғасы; R= $\sqrt{r^{2} + \frac{а^{2}}{4}} =$ $\sqrt{r^{2} + \frac{а^{2}}{4}} =$ R

r - ішт. сыз. ш. радиусы; т/к: R А В

= $\frac{\sqrt{4r^{2} + а^{2}}}{2};$ $\frac{\sqrt{4r^{2} + а^{2}}}{2};$ Жауабы: $\frac{\sqrt{4r^{2} + а^{2}}}{2};$ $\frac{\sqrt{4r^{2} + а^{2}}}{2};$

5. Ой сергіту - шығармашылықты шыңдау

Бұл жұмыс жұппен жүргізіледі, яғни екі оқушы бірігіп жасайды. Мультимедиада шығармашылық жұмыстың жүру барысы ретімен шығып отырады, әр кезеңді мұғалім тексеріп отырады.

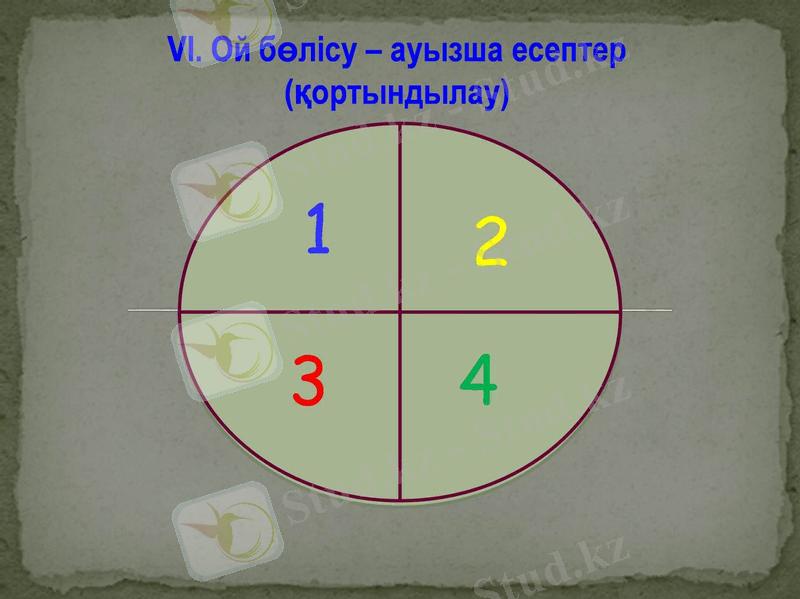
1 . Радиусы 10м болатын шеңбер ұзындығын тап. Жауабы: 20π м

2. Шеңбердің ұзындығы 1-ге тең. Радиусын тап. Жауабы: 1/(2π)

3. Катеттері 4дм және 3дм болып келген тік бұрышты үшбұрышқа сырттай сызылған шеңбердің ұзындығын тап. Жауабы: 5π дм

4. Квадраттың қабырғасы $2\sqrt{2}$ $2\sqrt{2}$ . Квадратқа іштей сызылған шеңбер радиусын тап. Жауабы: $\sqrt{2}$ $\sqrt{2}$

Бұл есептерді шығарып болған соң, экранда АРХИМЕД, ӘЛ-КӘШИ, ЛЕОНАРДО ЭЙЛЕР деген үш ғалымның аттары шығады. Олардың π санының математикаға енуіне жасаған жетістіктері туралы айтылады.

АРХИМЕД - π санының бастапқы 3 таңбасын дұрыс тапқан.

ӘЛ-КӘШИ - 16 таңбасын дұрыс тапқан, бірақ Еуропаға белгісіз болған.

ЛЕОНАРДО ЭЙЛЕР - 153 таңбасын дұрыс тапқан.

«Периферия» - грек сөзі дөңгелек ұғымын береді.

VII. Үйге тапсырма, бағалау

§13 (қайталау), №218, 223.

Атырау қаласы, Н. Тілендиев атындағы Кіші өнер академиясының математика

пәнінің 1 санатты мұғалімі - Есенғазиева Ақмарал Зейноллақызы

Ұқсас жұмыстар

Ең кіші ортақ еселікке есептер шығару: бекіту сабағы

Ондық бөлшектерді қосу бойынша есептер шығару сабағы

Проценттер арқылы экологиялық есептер шығару