8-сыныпта Қараевтың деңгейлеп-саралап оқыту элементтері негізінде өткізілген Квадрат теңдеулер тарауын қайталау-сайыс сабағы
Алматы облысы
Жамбыл ауданы
Қазыбек бек бекеті
Ұзынағаш орта мектебі Та
Таджимағамбетова Меңдігүл Валиқызы
II санатты математика пән мұғалімі
Оқушылардың алған білімдерін бекіту, жетілдіру мақсатында, әр оқушының білім деңгейлерін ескере отырып, Қараевтың деңгейлеп саралап оқыту технологиясының элементтерін қолданып «Квадрат теңдеулер» тарауын қайталау сабағын 8 сыныптарда сайыс түрінде өткізген сабағымды көрсеткелі отырмын. Сынып үш қатарға бөлінгені бойынша сайысқа түседі. Әр қатарда барлық деңгей есептерін шығара алатын оқушылар араласып отырады. Сабақ сергіту бөлімінен басталады.
1 кезең.
Қайталауға арналған сұрақтар:
1. Квадрат түбірдің анықтамасы?
2. Қандай теңдеулер толымсыз квадрат теңдеулер деп аталады?
3. Келтірілген квадрат теңдеу дегеніміз не ?
4. Квадрат теңдеудің формуласын кім жазады?
5. Дискриминанттық 3 жағдайын: D<0, D>0, D=0.
6. Виет теоремасын кім айтып, жазады?
2кезең.
Деңгейлік тапсырмалар :
1 деңгейдегі тапсырмалар - квадрат теңдеудің дискриминантын есептеп, қанша түбірі болатынын анықтауға арналған есептер.
Түбірлері х 1 мен х 2 болатын теңдеулерді жазыңдар:
2 -ші деңгейлік есептер.
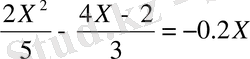
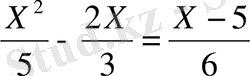
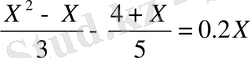
3- ші деңгейлік есептерге келтірілген квадрат теңдеулердегі белгісіз p немесе q мәндерін Виет теоремасы қоданып есептеуге арналған есептер.
x 2 + px -35=0;
x 1 =7; p=?.
x 2 - 13x - q=0
x 1 =12, 5; q=?
x 2 - px +5=0;
x 1 =5; p=?
Берілген теңдеулерде q-дың мәнін есептеу керек.
х 2 +4х+ q=0
х 1 - х 2 =6
х 2 -4х+ q=0
х 1 - х 2 =2
х 2 -12х+ q=0
х 1 - х 2 =2
Үш деңгейдің есетерін дұрыс шығарылуын тексеріле отырып, деңгей тапсырмасына қарай бағаланады.
3 кезең. Оқушыларға үлестірмелі тест тапсырмалары таратылады.
1нұсқа
А. 1
В. -2
С. 2
Д. 0
А. 1, 6; -1;
В. 1 ; -1, 6;
С. -5; 8;
Д. 8; -5
А. х 2 +4, 5х-2, 5= 0
В. х 2 +5, 5х-25= 0
С. х 2 -4, 5-2, 5= 0
Д. х 2 -4, 5х+2, 5= 0
2нұсқа
А. -1
В. 2
С. -3
Д. 3
А. 2 ; -2/3;
В. 2/3 ; -2;
С. 1 ; 1/3;
Д. -3 ; 0 ;
А. х 2 +3, 25х-7, 5= 0
В. х 2 - 3, 25х- 0, 75= 0
С. х 2 +3, 25х+7, 5= 0
Д. х 2 - 3, 25х+0, 75= 0
3нұсқа
А. 5
В. -5
С. 3
Д. -2
А. 1; 5/7;
В. -1 ; - 5/7;
С. 1; -5/7;
Д. -1; 5/7
А. х 2 +6, 2х-1, 2= 0
В. х 2 - 5, 8х- 1, 2= 0
С. х 2 -6, 2х+1, 2= 0
Д. х 2 +5, 8х- 1, 2= 0
Сабақты қорытындылай отырып оқушыларға тақтаға квадрат теңдеуді шешу жолдарын көрсетіп, тізбек құрастыруды сұрадым.
Квадрат теңдеу
Толымсыз түрі Толымды түрі
ах 2 =0 ах 2 +bx=0 ax 2 +c=0 ах 2 +bx+c =0
b=0; c=0; b=0; D=b 2 - 4ac
c=0; x=0;
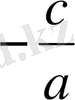>0; x
1/2
=
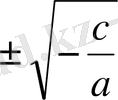; D>0, D=0, D<0;
x
1/2
=0; x=
;
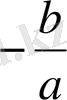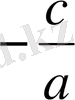<0; шешімі жоқ; x
1/2
=
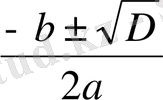х=
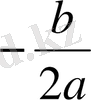; шешімі жоқ;
Үйге тапсырма : Кез келген екі санды квадрат теңдеудің түбірі деп алып бірнеше теңдеу құрып келу керек.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.
Ақпарат
Қосымша
Email: info@stud.kz