Функцияның экстремумдері

Функцияның экстремумдері

Математика пәнінің мұғалімі: Г.Прназарова

Сабақтың тақырыбы: Сындық нүктелер. Функцияның экстремумдері

Сабақтың мақсаты:
1. Оқушыларға тақырыпты игерте отырып , туындынының көмегімен функцияның
экстремум нүктелерін табу алгоритмін үйрету;
2. Оқушылардың математикалық таным көкжиегін дамыта , есеп шығару
дағдысын қалыптастыру;
3. Оқушылардың шығармашылық қабілеттерін арттыру.

Типі: Жаңа сабақтың игерту
Түрі: Интегралды сабақ

Пәнаралық байланыс: информатика , физика

Көрнекілігі: Интерактивті тақта, миниплакаттар , үлестірмелі карточкалар,
иллюстрация

Пайдаланған әдебиеттер: 10 сынып « Алгебра және анализ бастамалары»
2006ж
10-11 сынып « Алгебра және
анализ бастамалары» 2002ж
Интернет желісі

Барысы:
1. Ұйымдастыру кезеңі
2. Үй тапсырмасын тексеру
3. Өткен сабақты бекіту ( тест сұрақтары)
4. Жаңа сабақты меңгерту
5. Есептер шығару
6. Бекіту
7. Үйге тапсырма

І. Үй тапсырамсы
№263(ә)
F(x)= 2x3-3x2-12x-1;
F’(x)= 6x2-6x-12
x2-x-6>0
(x-3)(x+2)>0
(x-3)(x+2)=0
X1=-2
X2=3
Интервал әдісіне саламыз
+
- +
-2
3 х

Жауабы: (-∞;-2] және [3;+∞) аралғында функция өседі,
[-2;3] кемиді

ІІ. Өткен тақырыпқа шолу
Тесть сұрақтары
1. Функцияның туындысын тап
у = 2,5 х4 – 4 х3 + 7 х – 5.
1) у ´= 4 х3– 12 х2 + 7
2) у´ = 10 х3 – 12 х2 – 5
3) у´= 5 х3 – 3 х2 + 7
4) у´ = 10 х3 – 12 х2 + 7
Жауабы: 4
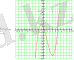
2. суретте у = f(х) графигі берілген.
Функцияның анықталу облысын анықта

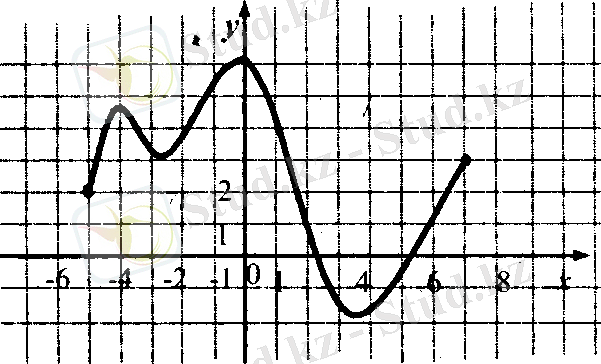
1) [- 5; 7]
2) [- 2; 6]
3) [- 2; 4]
4) [0; 7]

Жауабы:1

3. у = f(х) функцияның графигі [– 6; 4] аралықта.
f(х) >0 анықта

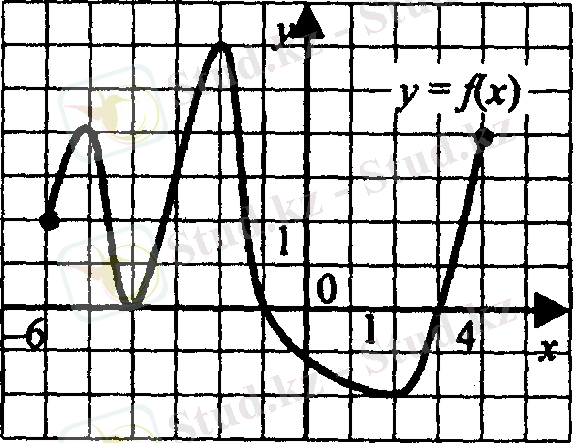
1) [- 6; - 5] [- 4; - 2] [2; 4]
2) [- 6; - 5] [- 4; 2] [3; 4]
3) [- 6; - 4) (- 4; - 1) (3; 4 ]
4)[- 6;- 1) (3;4]
Жауабы: 4

4.Функцияның қай аралықта кемімелі

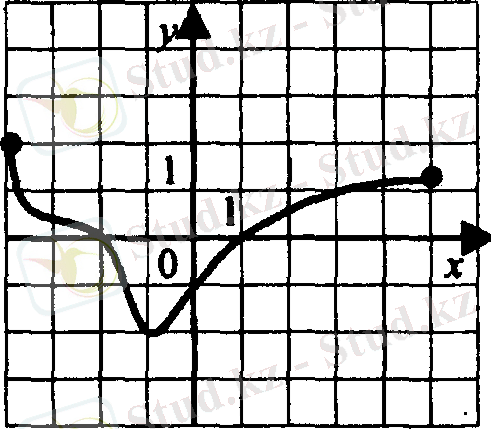
1)[– 4; 0]
2)[– 4; 1]
3)[– 2; 1]
4)[– 4;– 1]
Жауабы: 4

ІІІ.Жаңа сабақты меңгерту

Оқушыларға үлестірмелі карточкалар беріліп , ауызша жауап алынады.
Карточка №1
Y=(x-3)2(x-2) максимум және минимум нүтелерін тап.

Карточка №3 Y=х3-х2-3х максимум және минимум нүтелерін тап.

Осы сияқты №1-№15 үлестірмелі карточкалар

• Анықтама :
• Функцияның туындысы нольге тең немесе туындысы болмайтын анықталу
облысының ішкі нүктелері сындық нүктелер деп атайды.

• Қажетті шарты

• Егер f(x) функциясының х экстремум нүктесі болып және оны осы
нүктенің аймағында f’(x ) туындысы бар болса , онда ол туынды х
нүктесінде нөлге
тең , яғни f’(x )=0

• Жеткілікті шарты

• Егер х нүктесінде f(x) функциясы үзіліссіз, ал (а;х0 ) аралығында
f’(x)>0 (f’(x)<0)және (х0 ;b) аралығында f’(x)<0 (f’(x)>0 ) болса ,
онда х0 нүктесінде f(x) функцияның максимум (минимум) нүктесі болады.

х0 нүктесінің аймағында туынды таңбасы плюстен минуске ауыстырлыса ,
онда х0 нүктесі максимум нүтесі болады.

х0 нүктесінің аймағында туынды таңбасы минустен плюске ауыстырлыса ,
онда х0 нүктесі минимум нүтесі болады.

Функцияның экстремум нүктелерін табу алгоритмі

• 1. функцияның туындысын табу;
• 2.функцияның сындық нүктелерін табу, яғни f’(x)=0 теңдеуін шешу;
• 3. сындық нүктелер аймағында f’(x) тыундының таңбасын интервалдар
әдісімен анықтау;
• 4.экстремум нүтелерінің бар болуының жеткілікті шартын ,қолданып
максимум және минимум нүктелерін табу.

ІV. Есептер шығару
А-тобы
№267 есеп (ауызша )
№268 Функцияның экстремум нүктелерін анықтаңдар

А) f(x)=2x2-3x+1
1) f’(x)=(2x2-3x+1)’=4x-3
2) f’(x)=0 ;
4x-3=0
4x=3
x=3/4
- +
3)

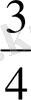
4) Жауабы: xmin=.

5) ә) f(x)=x2-2x+.

f’(x)=(x2-2x+)’=2х-3 ; 2x-2=0
2x=2
X=1
- +

1
Жауабы:
Xmin=1
№269

а) f(x)=-3x2+13x-12
f’(x)=(-3x2+13x-12)’=-6x+13
-6x+13=0
-6x=-13
X=

+ -

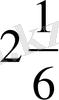
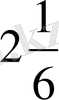
Жауабы: Xmax=

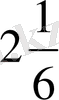
ә) f(x)=4-8х-5x2
f’(x)=(4-8х-5x2)’=-8-10x
-8-10x=0 +
-
-10x=8 -

X=-; Жауабы: Xmax=-
В тобы
№274 Функцияның максимум және минимум нүктелерін табыңдар:
ә) f(x)=16x3-15х2-18х+6
f’(x)=(16x3-15х2-18х+6)’=48x2-30x-18
x1=1; x2=0,375

+ -
+
0,375 1
xmin=1
xmax=0,375

ҰБТ –дан келетін дайындық тест тапсырмасынан

1. Функцияның неше экстремум нүктелері бар у = 3х5 – 15х2.
Ответы: 1) 0 2) 1 3) 2 4) 3 5) 4
Шешуі:
у ' =15х4 – 30х
15х ( х3 - 2) = 0 у '
+ - +
х = 0, х = 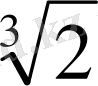- экстремум нүктелері
___________________________________ х
у

Жауабы: 3
Бекіту:

|Білемін |Білдім |Үйрендім |Таң қалдырды |
| | | | |

Үйге тапсырма :
№270, №274 (а,в)