10-сынып: Алгебра және анализ бастамалары - тригонометриялық қосынды мен айырымды көбейтіндіге түрлендіру, күрделі функцияның туындысы және теңдеулерді функциялық әдіспен шешу бойынша сабақ жоспары


 Жамбыл облысы
Жамбыл облысы
Жамбыл ауданы
А. С. Макаренко орта мектебінің жоғары
санаттағы математика пәнінің мұғалімі.
Сыныбы: 10(жаратылыстану -математикалық бағыты)
Пәні: алгебра және анализ бастамалары.
Сабақтың тақырыбы : Қосынды және айырым түрінде берілген тригонометриялық функцияларды көбейтіндіге түрлендіру.
Сабақтың мақсаты: Қосынды және айырым түрінде берілген тригонометриялық формулалармен таныстырып, ол формулаларды есептер шығаруда қолдану дағдысын қалыптастыру .
Сабақтың көрнекілігі : Тригонометриялық тепе - теңдіктер (таблица)
тест тапсырмалары, карточкалар.
Сабақтың түрі : жаңа сабақ.
Сабақтың әдістері : сұрақ-жауап, лекция, карточкамен жұмыс.
Сабақтың барысы: 1. Ұйымдастыру кезеңі.
2. Тригонометриялық тепе-теңдіктерді қайталау.
(Жаңа сабақты өтуге дайындық)
Кейбір бұрыштардағы тригонометриялық функциялардың мәндерін есте сақтау үшін мына тәсілді қолдануға болады
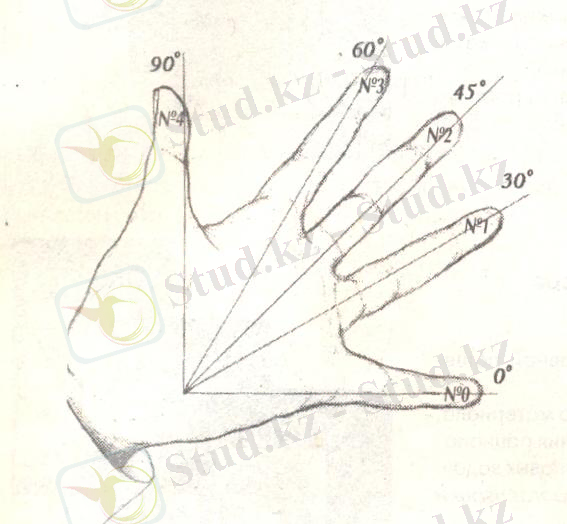
Енді осы тәсілді есте сақтағанымызды тексеріп көрейік
\[t g\,60^{0}\cdot c t g\,60^{0}\]
Шешуі: А, В, С. Д, Е, А.
Тапсырманың шешімін инемен тесу тәсілімен тексеріп, нәтижесі бірден айтылады.
3. Жаңа сабақ.

Сонымен,
Енді осы формулаларды есептер шығаруда қолдануды үйренейік:
1) Өрнектің мәнін табу керек
2) Тепе - теңдікті дәлелдеу керек
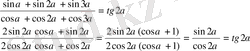
3) Өрнекті ықшамдау керек:
4. Жаттығу есептерін шығару . №54(а, ә)
а) =
ә)
№56(а)
а) + = =-
№59(а)
№61(а)
№62(а)
5. Сабақты қорытындылау.
Аргументтері әртүрлі синустар мен косинустардың айырымын немесе көбейтіндіге жіктеудің мақсаты неде?
Аргументтері әртүрлі синус пен косинустың айырымын немесе қосындысын көбейтіндіге қалай келтіруге болады?
6. Үйге тапсырма.
№63, 64 жаттығулар, аргументтері әртүрлі тангенс пен котангенстің айырымын немесе қосындысын көбейтіндіге келтірудің формулаларын қорытып шығару.
Сабақтың тақырыбы : Күрделі функцияның туындысы.
Сабақтың мақсаты :
а) оқушыларға күрделі функция ұғымын, оның туындысын есептеу формуласын меңгерту;
күрделі функция туындысын есептеу бойынша оқушылардың білік, дағдыларын қалыптастыру;
б) ойлау жүйелілігін және талдау, салыстыра білу қабілетін дамыту;
в) іздену, бақылау арқылы оқушылардың дүние таным қабілеттерін қалыптастыру.
Құрал-жабдықтар, көрнекті құралдар: тақырып бойынша
таблицалар(туынды табу ережелері, туынды табу
формулалары), жаңа сабақ бойынша мысалдар,
тест тапсырмалары.
Сабақтың типі: Жаңа білім беру
Сабақтың әдісі: түсіндірмелі, практикалық.
Сабақтың барысы:
I . Ұйымдастыру кезеңі . Оқушыларды түгелдеп,
сабаққа назарын аудару. Сабақтың жоспарымен,
бағалау шкаласымен таныстыру.
II. Үй тапсырмасын тексеру . 1) №203(а, ә) ; №204(б)
. №203(а, ә)
а) f(x) =x 4 ; x 0 =-1
y= f(x 0 ) + f
f(x 0 ) =(-1) 4 =1 f 1 (x) =4x 3 f 1 (-1) =4
ә) f(x) =х-3x 2 ; x 0 =2
f(x 0 ) =2-3
№204(б)
f(x) =3-х 2 +х 4 а =-1
y= f(x 0 ) + f
f(x 0 ) =3-1+1 =3 f 1 (x) = -2х+4x 3 f 1 (-1) =2+4
2) Математикалық диктант.
1.
2.
3.
4.
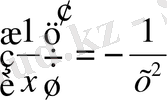 9.
9.
5.
Орындалуын тексеру: тақтадағы есепті тексеру үшін дұрыс жауабы ілінеді. Оқушы өзін-өзі тексереді.
Орында отырған оқушылардың жұмыстарын жинап алып тақтаға дұрыс жауабы ілінеді, бірден алған ұпайлары жарияланады.
III. Жаңа сабақ.
а) Туындының көмегімен күрделі теңдеулерді шешуге, физикада жылдамдық пен үдеуді есептеуге, геометрияда жанаманың теңдеуін анықтауға және де білімнің басқа салаларында да пайдаланылады .
Осы уақытқа дейін элементар функциялардан туынды алып үйрендік . Бүгінгі сабақта күрделі функция ұғымымен және оның туындысын есептеу формуласын пайдаланып есептер шығаруды үйренеміз.
б) Күрделі функция деп y=f(u) : u€U; y€Y u=g(x) x€X
y=f(g(x) ) функциясы аталады.
y= f(g(x) ) күрделі функцияның жалпы түрі
u=g(x) күрделі функцияның ішкі бөлігі, ал y=f(u) сыртқы бөлігі деуге болады.
Енді күрделі функцияның ішкі және сыртқы бөлігін ажыратуға бірнеше мысал келтірейік:
y=f(u) u=g(x)
1. u=
2. y=sin(3x-
3. y=
Күрделі функцияның туындысытабу ережесі:
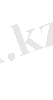
Осы формуланы пайдалануға мысал келтірейік:
y=(5+2x
3
)
7
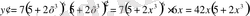
y =
iV. Жаңа сабақты бекіту Күрделі функцияның туындысын табу жұмыртқаның бөліктері ретінде қарастырып,
сыртқы бөлігінен туынды алу, «қабығын ашу» ретінде қарастыру бірақ ақ уызы мен сары уызы өзгеріссіз қалады, яғни:
V . Жаттығу есептерін шығару
. №213(а, б) №214(а, б) №215(а, б)
№ 213 Күрделі функциясын құрайтын функцияларды анықта:
a) y=(x+3) 2 ; х+3 функцияның ішкі бөлігі; y=u 2 фунцияның сыртқы бөлігі
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz