ҰБТ-ке дайындық: стереометрия есептері мен шешімдері


Батыс Қазақстан облысы
Теректі ауданы
Федоровка қазақ жалпы орта білім беретін мектебі
ҰБТ -ке дайындық
( стреометрия курсының есептерінің шығару жолдары)
Айнагүл Хабиболлақызы Хайрова
І санатты математика және информатика пәнінің мұғалімі
2011-2012 оқу жылы
Федоровка қазақ жалпы орта білім беретін мектебінің І санатты математика және информатика пәнінің мұғалімі Айнагүл Хабиболлақызы Хайрованың
«ҰБТ -ке дайындық» ( стреометрия курсының есептерінің шығару жолдары) жинағына
Пікір
Есептер жинағында, бірнеше жылдардан бері ҰБТ-де кездесіп отырған стреометрия курсы есептерінің шығару жолдары және оларға сәйкессызбаларымен көрсетілген.
Жинақ 8 бөлімнен тұрады. Әр бөлімге қысқаша анықтамалық мәліметтер мен формулалар берілген. Құрастырылған есептер жинағы ҰБТ-ке даярланушыларға, өз беттерімен жұмыстану барысында үлкен көмек көрсетеді.
Мұғалімнің «ҰБТ -ке дайындық» есептер жинағы талапқа сай орындалған және бекітуге ұсынылады.
Пікір айтушы: Федоровка қазақ жалпы орта білім беретін мектебінің жоғары санатты математика пәнінің мұғалімі Р. З. Кулекешова
І бөлім Жазықтықтардың қасиеттері
2003ж
№1(4 нұсқа №28)
А нүктесі жазықтықтан 18 см қашықтықта жатыр. Осы нүктеде өтетін және жазықтықпен 60 0 бұрыш жасайтын көлбеудің ұзындығын табыңыз.
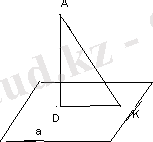 AD=18, <AKD=60
0
AD=18, <AKD=60
0
AK-?
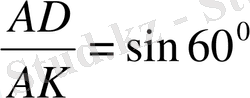
AK=18
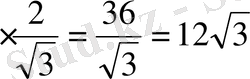
2004 ж
№2. (12 нұсқа №28)
АВС үшбұрышы a жазықтығындағы MNK үшбұрышының проекциясы, D нүктесі АВ кесіндісінде жатыр. А, В, С және D нүктелері сәйкеc M, N, K, P нүктелерінің прокциялары.
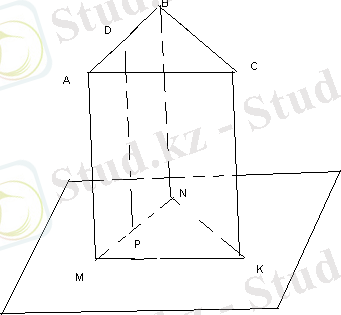 Егер АD =4, DB=6, MK= 6 болса, онда MN кесіндісінің ұзындығын табыңыз.
Егер АD =4, DB=6, MK= 6 болса, онда MN кесіндісінің ұзындығын табыңыз.
АD =4,
DB=6,
MK= 6
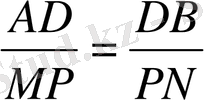
PN=9,
MN=6+9=15
№3 (21 нұсқа №28)
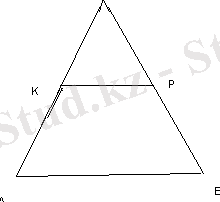 АВС үшбұрышының АВ қабырғасына параллель а жазықтығы оны АС және ВС түзулерінде жататын К және Р нүктелерінде қиып өтеді. Егер AC= 15, AB= 20, KP=4 болса, КС -ны табыңыз.
АВС үшбұрышының АВ қабырғасына параллель а жазықтығы оны АС және ВС түзулерінде жататын К және Р нүктелерінде қиып өтеді. Егер AC= 15, AB= 20, KP=4 болса, КС -ны табыңыз.
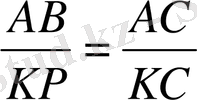
KC=3
№4 (26 нұсқа №28)
Ұзындығы 10 см тең кесінді жазықтықты қиып өтеді. Оның ұштары жазықтықтан 3 см және 2 см қашықтықта жатыр. Берілген кесінді мен жазықтықтың арасындағы бұрышты табыңыз
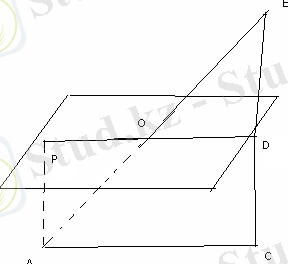
АВ=10см
АР=2см
ВD=3см
<BOD-?
BC=BD+DC=2см+3см=5см
<BAC=<BOD=

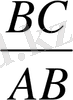 =sin
=sin

Sin
 =
=
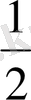
 =30
0
=30
0
<BOD=30
0
2006 ж
№5 (14 нұсқа №24)
Ұзындығы 2, 4 см-ге тең ВК кесіндісі катеттері 6 см және 8 см болатын АВС тік бұрышты (<B=90 0 ) үшбұрышының жазықтығына перпендикуляр. К нүктесінен АС түзуіне дейінгі қашықтықты табыңыз.
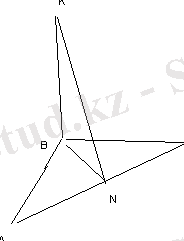 AB=6, BC=8, BK=2, 4
AB=6, BC=8, BK=2, 4
KN-?
AN=x
NC=10-x
BN 2 =AB 2 -AN 2
BN 2 =BC 2 -NC 2
36-x 2 =64-(10-х) 2
20х=7, 2
Х=3, 6
BN 2 =36-3, 6 2
BN=4*8
KN
2
=BK
2
+BN
2
KN 2 =5, 76+23, 04=28, 8
KN=2, 4
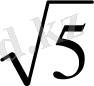
№6
Бір нүктеден өтетін екі көлбеудің ұзындықтары 10 см және 17 см. Берілген нүкте жазықтықтан 8 см қашықтықта болса, көлбеулердің проекцияларын табыңыз.
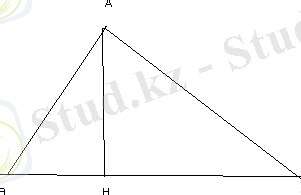 AB=10, AC=17, AH=8
AB=10, AC=17, AH=8
BH, HC-?
BH 2 =AB 2 -AH 2
BH 2 =100-64=36
BH=6
HC 2 =AC 2 -AH 2
HC
2
=289-64=225
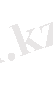
HC=15
2009ж
№7(22 нұсқа №19)
АВ кесіндісі а жазықтығын қияды. С нүктесі АВ кесіндісінің ортасы. А, В және С нүктелері арқылы
 жазықтығын М, К және Р нүктелерінде қиятын параллель түзулер жүргізілген.
жазықтығын М, К және Р нүктелерінде қиятын параллель түзулер жүргізілген.
Егер АM=
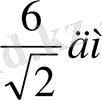 , BP =
, BP =
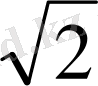 дм болса, СK кесіндісінің ұзындығын табыңыз.
дм болса, СK кесіндісінің ұзындығын табыңыз.
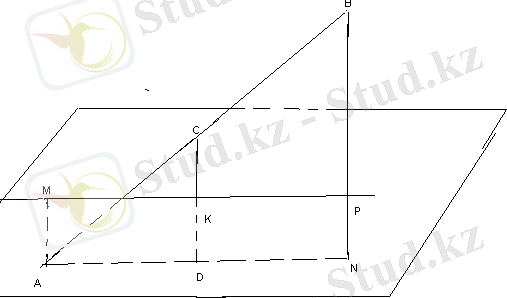 BN= BP+PN
BN= BP+PN
BN=
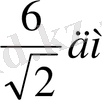 +
+
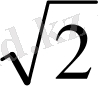 дм=4
дм=4
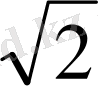 дм
дм
АВN үшбұрышының орта сызығы- CD
СD=BN:2=2
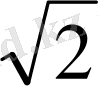
CK=CD-KD=2
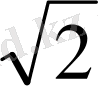 -
-
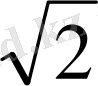 =
=
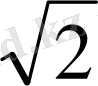
№8 (1 нұсқа №19)
А(3; -2; -4) нүктесінен ОУ осіне дейінгі және А нүктесінен XOZ жазықтығына дейінгі қашықтықтар қосындысын табыңыз.
A(3; -2; -4)
ОУ осіндегі А 1 (0; -2; 0)
XOZ жазықтығындағы А 2 (3; 0; -4)
АА
1
=
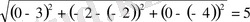
АА
2
=
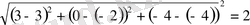
АА 1 + АА 2 =5+2=7
№9 (7 нұсқа №24)
АВСD ромбының қабырғасы 8 см, ал <D=135
0
, AE
 ABCD және ВС түзуінен 8
ABCD және ВС түзуінен 8
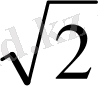 қашықтықта жатыр. В, С және Е нүктелері арқылы өтетін жазықтық пен ромб жазықтығының арасындағы бұрышты табыңыз.
қашықтықта жатыр. В, С және Е нүктелері арқылы өтетін жазықтық пен ромб жазықтығының арасындағы бұрышты табыңыз.
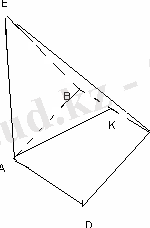
AB=8, EK=8
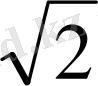
S ромб =a 2 sin135 0
S=32
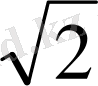
S=ah
h=S:a=4
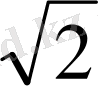
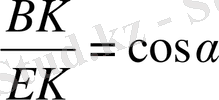
cos
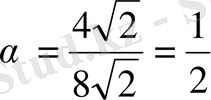
 =60
2
=60
2
№10 (19 нұсқа №19)
АВСD ромбының қабырғасы 8 см, ал <А=45
0
Ромб жазықтығына ВЕ перпендикуляры тұрғызылған. Е нүктесі АD түзуінен 4
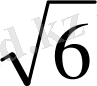 қашықтықта. Е нүктесінен АВС жазықтығына дейінгі қашықтықты табыңыз.
қашықтықта. Е нүктесінен АВС жазықтығына дейінгі қашықтықты табыңыз.
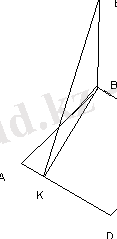 AB=8, EK=4
AB=8, EK=4
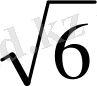
<A=45 0
<ABK=45 0
AK 2 +KB 2 =AB 2
2KB 2 =64
KB 2 =32
BE 2 =EK 2 - KB 2
BE 2 =96-32=64
BE=8
ІІ бөлім. Пирамида
Пирамида деп бір жағы кез келген көпбұрыш, ал қалған п жағы төбелері ортақ үшбұрыштардан тұратын көпжақты атайды.
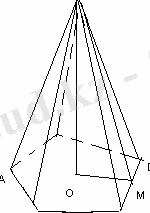 SA
-
бүйір қыры
,
SO-биіктігі, SM-бүйір жағының биіктігі( апофемасы)
SA
-
бүйір қыры
,
SO-биіктігі, SM-бүйір жағының биіктігі( апофемасы)
V- көлемі
S т. б -толық бетінің ауданы
S таб -табанының ауданы
S б. б -бүйір бетінің ауданы
Кез келген пирамида үшін: V=
 S
таб
H
S
таб
H
S т. б = S б. б + S таб
Дұрыс пирамида үшін
:
S
б. б
=
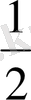 PA
PA
P-пирамида табанындағы көпбұрыштың периметрі
А-апофемасы
Қиық пирамида деп пирамиданың табаны мен табан жазықтығына параллель қима жазықтық арасындағы бөлігі аталады.
Р 1 , Р 2 -табандарының периметрі
S 1, S 2 -табандарының аудандары
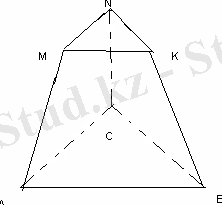
V=
 H(S
1
+S
2
+
H(S
1
+S
2
+
 )
)
S
б. б
=
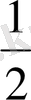 (P
1
+P
2
) A
(P
1
+P
2
) A
2003 ж тест жинағы
№1 (1 нұсқа №12)
Егер берілген нүктеден барлық қабырғаларына дейін 3 см, ал үшбұрыш қабырғасы 2
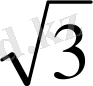 см тең болса, берілген нүктеден дұрыс үшбұрыш жазықтығына дейінгі қашықтықты табыңыз.
см тең болса, берілген нүктеден дұрыс үшбұрыш жазықтығына дейінгі қашықтықты табыңыз.
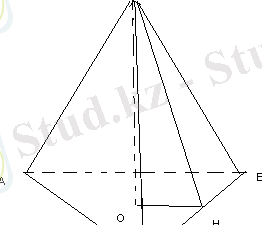 SH=3 см
SH=3 см
AB= 2
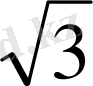 см
см
SO=?
 Шешуі: OH - дұрыс үшбұрышқа іштей сызылған шеңбердің радиусы.
Шешуі: OH - дұрыс үшбұрышқа іштей сызылған шеңбердің радиусы.
r=
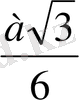 ;
;
OH=
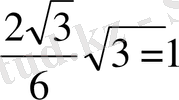
SO 2 =SH 2 -OH 2
SO=
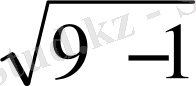 =2
=2
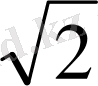
Жауабы:2
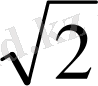 см
см
№2. (1 нұсқа №21)
Пирамиданың табанына параллель жазықтық пирамида биіктігін 3:2 қатынасқа бөледі. Жазықтық пирамиданың көлемін қандай бөлікке бөледі?
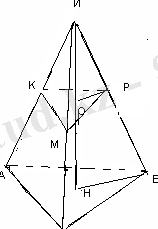
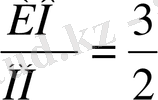
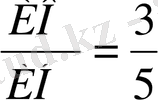 ИО=3x, ОН=2x
ИО=3x, ОН=2x
S КМР =S 1 ; S ABC = S 2
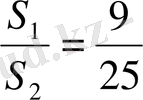 S
1
=9y; S
2
= 25y
S
1
=9y; S
2
= 25y
V
ИКМР
=
 Equation. 3 ИО* S
1
=
Equation. 3 ИО* S
1
=
 Equation. 3 *3x*9у=9 ху
Equation. 3 *3x*9у=9 ху
V
қиық пир
=
 ОИ (S
1
+S
2
+
ОИ (S
1
+S
2
+
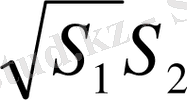 ) =
) =
 *2x (9y+25y+
*2x (9y+25y+
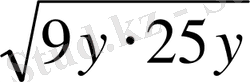 ) =
) =
 *98 xy
*98 xy
 =
=
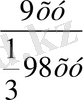 =
=
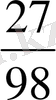
№3 (2 нұсқа №10)
Төртбұрышты дұрыс пирамиданың биіктігі 2 см -ге тең, ал табанының қабырғасы 4 см. Бүйір қырының ұзындығын тап.
SH=2, AB= 4. SA= ?
АC=
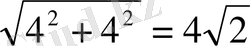
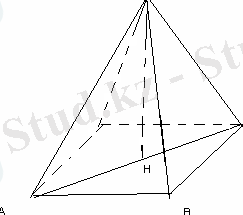 AH=2
AH=2
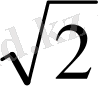
SA=
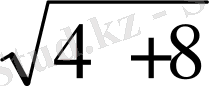 =
=
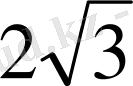
Жауабы:
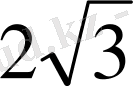 см.
см.
№4 (2 нұсқа №21)
Төртбұрышты дұрыс пирамиданың биіктігі 9 см-ге тең, ал бүйір қыры 12 см болса, көлемі неге тең?
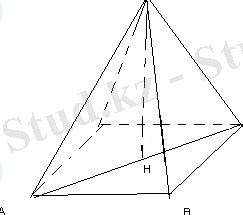 SH=9 см, SA= 12 см, V=?
SH=9 см, SA= 12 см, V=?
НС=
 =3
=3

AC=6

AB 2 +BC 2 =252
S=AB 2 = 126
V=
 S H
S H
V=
 *126 *9=378см
3
Жауабы:378см
3
*126 *9=378см
3
Жауабы:378см
3
№5 (4 нұсқа № 21)
Дұрыс төртбұрышты пирамиданың биіктігі 80 см, табан қабырғасы 120 см. Табанының центірінен өтетін бүйір жағына параллель қимасының ауданын табыңыз.
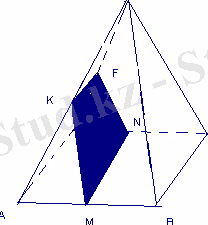
SH=80 cм,
AB=120 cм
S KFNM -?
AC=

AH=60
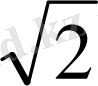
SA=
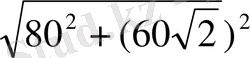 =20
=20

КМ=SA:2=20
 :2=10
:2=10

MN=BC=120
MO=(MN-KF) :2=(120-60) :2=30
KO=
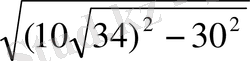 =50
=50
S
KFNM
=
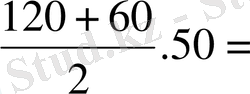 4500cм
2
4500cм
2
№6 ( 5 нұсқа № 10)
Төртбұрышты дұрыс пирамиданың табан қабырғасы 20 см, бүйір қырының екі жақты бұрышы 120 0 . Пирамиданың бүйір бетінің ауданын табыңыз.
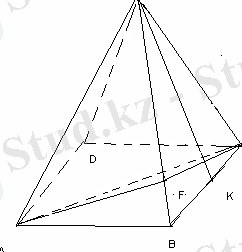
<AFC=120 0
AC 2 =AB 2 +BC 2
1)
 ABC
ABC
AC=
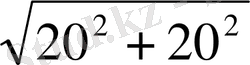 =20
=20
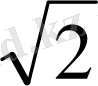
2)
 AFC
AFC
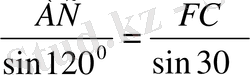
FC=(20
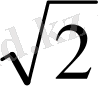 .
.
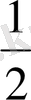 ) :
) :
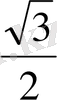 =20
=20
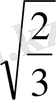
3)
 FBC
FBC
BF=
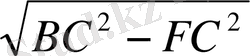 =
=
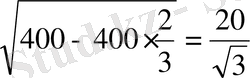
SC 2 =SF 2 +FC 2
SC=x,
SF= x-
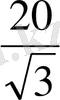
X
2
=( x-
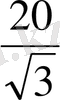 )
2
+(20
)
2
+(20
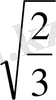 )
2
)
2
X
2
=X
2
-2X
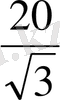 +(
+(
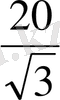 )
2
+
)
2
+
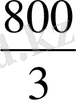
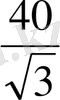 X=
X=
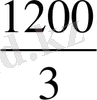
X=10
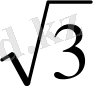
SC=10
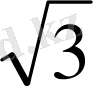
SK
2
=SC
2
-KC
2
=(10
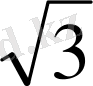 )
2
-10
2
=200
)
2
-10
2
=200
SK=10
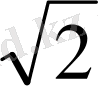
S
б. б
=
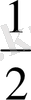 P
ABCD
SK=
P
ABCD
SK=
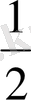 *80* 10
*80* 10
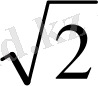 = 400
= 400
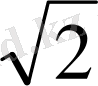
№7 (5 нұсқа № 21)
Үшбұрыш пирамиданың бүйір қырлары өзара перпендикуляр және 4 см, 5см, 6 см тең. Көлемі неге тең?
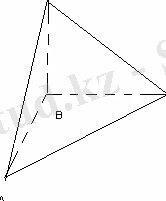
SB-биіктік,
AB=4 cм, BC= 5 cм, SB=6 cм
S
ABC
=
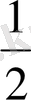 AB*BC=
AB*BC=
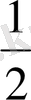 *4*5=10
*4*5=10
V=
 S
ABC
. SB=
S
ABC
. SB=
 *10*6=20 cм
3
*10*6=20 cм
3
№ 8 (7 нұсқа № 21)
Пирамиданың табаны - бүйір қабырғасы 10 см, табаны 12 см болатын тең бүйірлі үшбұрыш. Бүйір жақтары табан жазықтығымен 60 0 -қа тең екі жақты бұрыш жасайды. Пирамиданың биіктігін табыңыз.
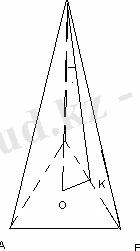
 ABC-тең бүйірлі, AC=CB=10 cм, AB=12 cм.
ABC-тең бүйірлі, AC=CB=10 cм, AB=12 cм.
<SKO=60 0 , SO-?
S=r p
KO=r=S:p
p=(10+10+12) :2=16
S=
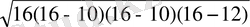 =48
=48
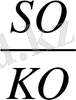 =tg60
0
=tg60
0
r=КО=48:16=3
SO=3
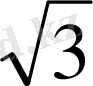 cм
cм
№9 (8 нұсқа №30)
Табанының қабырғасы 9 см және биіктігі 10 см болатын үшбұрышты дұрыс пирамидаға сырттай шар сызылған. Шардың радиусын табыңыз.
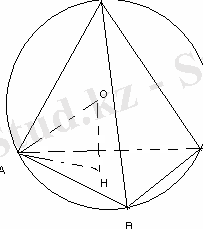 AH= r-
AH= r-
 ABC-ға сыртай сызылған шеңбердің радиусы
ABC-ға сыртай сызылған шеңбердің радиусы
AO=R -пирамидаға сырттай сызылған шардың радиусы.
SH-пирамиданың биіктігі.
R=
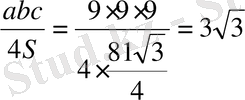
AS=
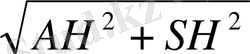 =
=
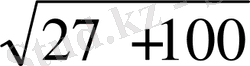 =
=
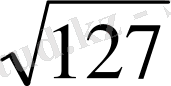
AS=L
L 2 =2RH
R=
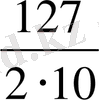 =6, 35
=6, 35
№10 (10 нұсқа №21)
Пирамиданың табаны -ромб, оның сүйір бұрышы 60 0 , қабырғасы 14 см. Пирамида табанындағы екі жақты бұрыштары 45 0 -тан. Пирамиданың көлемі неге тең?
ABCD-ромб, <A=60 0 <SKO=45 0 , V-?
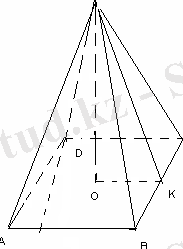 S
ромб
=a
2
sin 60
0
=14
2
*
S
ромб
=a
2
sin 60
0
=14
2
*
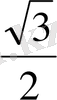 =98
=98
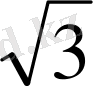
 AHD
AHD
DH = sin60 0
AD
DH=14 *
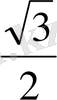 =7
=7
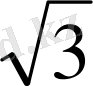
OK=DH:2=
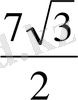
SO=OK
 SOK, <O=90
0
.
SOK, <O=90
0
.
<K=<S=45 0
V=
 S
ромб
SO=
S
ромб
SO=
 *98
*98
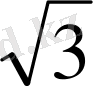 *
*
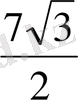 =343 cм
2
=343 cм
2
№11 (11 нұсқа №10)
Бүйір қыры 3см-ге, ал табанының қабырғасы 4 см-ге тең төртбұрышты дұрыс пирамиданың көлемін табыңыз.
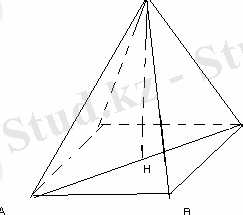 SA=3 cм, AB=4 cм, V-?
SA=3 cм, AB=4 cм, V-?
AC=
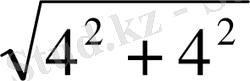 =4
=4
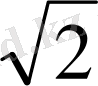
HC=AC:2=4
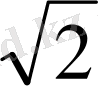 :2=2
:2=2
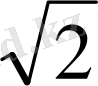
SH=
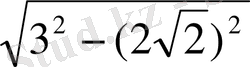 =1
=1
V=
 AB
2
SH=
AB
2
SH=
 *16*1=5
*16*1=5
 cм
3
cм
3
№12 (13 нұсқа №10)
Дұрыс төртбұрышты пирамиданың бүйір қыры 5 см, ал биіктігі 4 см. Пирамиданың көлемі неге тең?
SA=5 cм, SH=4 cм.
 V-?
V-?
HC=
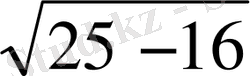 =3
=3
AC=2HC=6
AB 2 +BC 2 =AC 2
AB 2 =6:2=3
V=
 AB
2
SH=
AB
2
SH=
 *3*4=4 cм
3
*3*4=4 cм
3
№13 ( 14 нұсқа №12)
Берілген нүктеден шаршының барлық төбелеріне дейінгі қашықтық 4 см-ге тең. Ал шаршының қабырғасы 2 см-ге тең болса, берілген нүктеден шаршының жазықтығына дейінгі қашықтықты табыңыз.
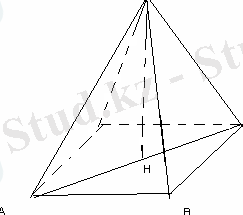 SA=SB=SC=SD=4 cм,
SA=SB=SC=SD=4 cм,
AB=2, SH-?
AB 2 +BC 2 =AC 2
AC=
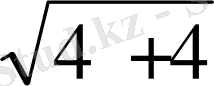 =2
=2
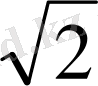
HC=
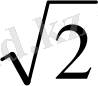
SH=
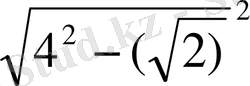 =
=
 cм.
cм.
№14 (17 нұсқа №21)
Төртбұрышты дұрыс пирамиданың бүйір бетінің ауданы 2
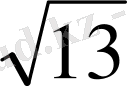 см-ге,
см-ге,
табанының қабырғасы 2 см-ге тең. Пирамиданың көлемі неге тең?
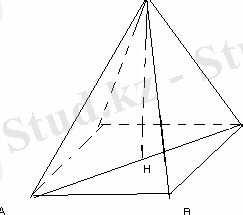 S
б. б
=2
S
б. б
=2
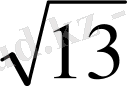 cм,
cм,
AB=2cм.
V-?
S
б. б
=
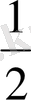 P
ABCD
. SM,
P
ABCD
. SM,
SM- бүйір жағының апофемасы
SM=2S
ABCD
:P=4
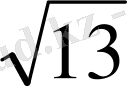 :8=
:8=
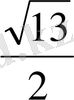
SH=
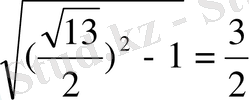
V=
 *4*
*4*
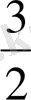 =2 cм
3
=2 cм
3
№15 (23 нұсқа №19)
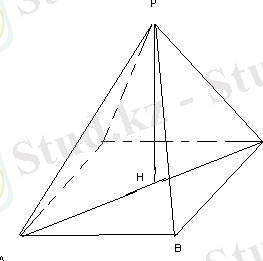 Төртбұрышты дұрыс пирамиданың бүйір қыры мен табанының арасындағы бұрыш
Төртбұрышты дұрыс пирамиданың бүйір қыры мен табанының арасындағы бұрыш
 , диогональдық қимасының ауданы S. Пирамиданың көлемі неге тең?
, диогональдық қимасының ауданы S. Пирамиданың көлемі неге тең?
<SAH=

S ASC =S, V-?
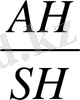 =ctg
=ctg

SH=h
AH=hctg

AC=2hctg

AB 2 +BC 2 =AC 2
2AB
2
=(2hctg
 )
2
)
2
AB
2
=2h
2
ctg
2

S
ASC
=
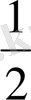 AC* SH=
AC* SH=
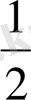 *2hctg
*2hctg
 *h=h
2
ctg
*h=h
2
ctg

h=

AB=
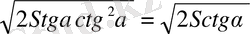
S
ABCD
=(
 )
2
=2Sctg
)
2
=2Sctg
 V=
V=
 2Sctg
2Sctg

 =
=
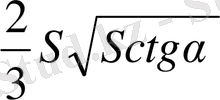
№16 (29 нұсқа №21)
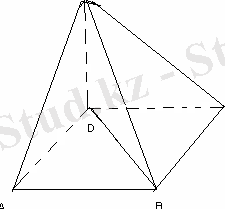 Пирамиданың табаны квадрат. Биіктігі табанының бір төбесі арқылы өтеді. Егер табанының қабырғасы 20 дм, биіктігі 21 дм болса, онда пирамиданың бүйір бетінің ауданын табыңыз.
Пирамиданың табаны квадрат. Биіктігі табанының бір төбесі арқылы өтеді. Егер табанының қабырғасы 20 дм, биіктігі 21 дм болса, онда пирамиданың бүйір бетінің ауданын табыңыз.
ABCB-шаршы, АB=20 дм, SD=21 дм. S б. б -?
S
ASD
=
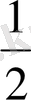 AD SD=
AD SD=
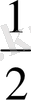 *20*21=210
*20*21=210
S
ABS
=
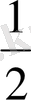 AB AS=
AB AS=
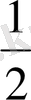 *20*29=290
*20*29=290
S б. б =2 (S ASD + S ABS ) =(210+290) *2=1000 дм 2 =10м 2
№17 (34 нұсқа №8)
Жазықтықта тік бұрышты үшбұрыш берілген. Гипотенузасы 12 см. Кеңістікте берілген бір нүктеден үшбұрыш төбелеріне дейінгі қашықтық 10 см-ден. Үшбұрыш жазықтығынан кеңістіктегі нүктеге дейінгі қашықтықты табыңыз.
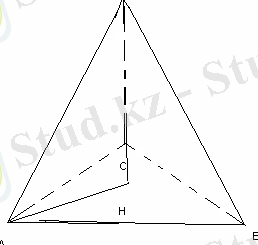
 ABC-тік бұрышты үшбұрыш, АВ=12 cм,
ABC-тік бұрышты үшбұрыш, АВ=12 cм,
SA=10cм
SH-?
AH=R-
 ABC-ға сырттай сызылған шеңбердің радиусы
ABC-ға сырттай сызылған шеңбердің радиусы
R=
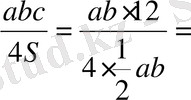 6
6
SH=
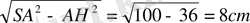
№18 (34 нұсқа №19)
Пирамиданың табаны диогональдары 4 см және 2
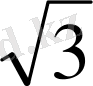 см арасындағы бұрышы 30
0
-қа тең параллелограмм. Пирамиданың биіктігі табанының кіші қабырғасына тең болса, онда көлемі неге тең?
см арасындағы бұрышы 30
0
-қа тең параллелограмм. Пирамиданың биіктігі табанының кіші қабырғасына тең болса, онда көлемі неге тең?
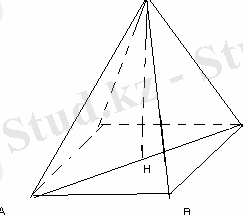 ABCD-параллелограмм, AC=4cм, BD=2
ABCD-параллелограмм, AC=4cм, BD=2
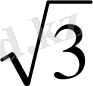 cм, <BHC=30
0
cм, <BHC=30
0
SH=AB, V-?
S=
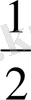 AC* BD *sin30
0
=
AC* BD *sin30
0
=
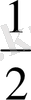 *4*2
*4*2
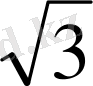 *
*
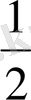 =2
=2
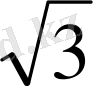 cм
2
cм
2
AB=
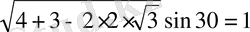
V=
 *2
*2
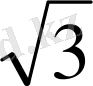 *1=
*1=
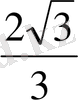 cм
3
cм
3
2004 жыл №19 (4 нұсқа №26)
ABCD тік төртбұрышының D төбесі арқылы тік төртбұрыш жазықтығына перпендикуляр DS түзуі жүргізілген. S нүктесінен тік төртбұрыштың төбелеріне дейінгі қашықтықтар
12 м, 14 м, 18 м. DS кесіндісінің ұзындығы неге тең?
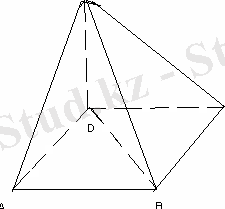 SA=12 м, SB=14 м, SC=18м
SA=12 м, SB=14 м, SC=18м
SD=?
AB=x, BC=y, SD=z
X 2 +z 2 =144
Y 2 +z 2 =196
X 2 +y 2 +z 2 =324
144-z 2 +196-z 2 +z 2 =324
Z 2 =16
Z=4м
Жауабы: SD=4м
№20
Үшбұрышты дұрыс пирамиданың бүйір қырының ұзындығы
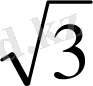 см-ге тең. Бүйір қыры табан жазықтығымен 60
0
бұрыш жасаса, онда пирамидаға сырттай сызылған шардың радиусын табыңыз.
см-ге тең. Бүйір қыры табан жазықтығымен 60
0
бұрыш жасаса, онда пирамидаға сырттай сызылған шардың радиусын табыңыз.
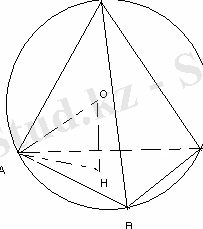 SA=
SA=
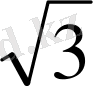 см
см
<SAH=60 0
AO=R- пирамидаға сырттай сызылған шардың радиусы
 =cos60
0
=cos60
0
AH=
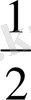
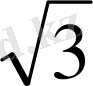 .
.
SH=
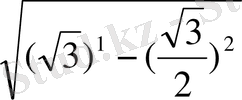 =
=
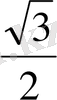
SA 2 =2R*SH
R=
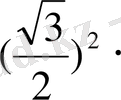
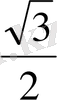 =
=
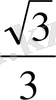 см
см
2005 ж
№21 (4 нұсқа №30)
Дұрыс тетраэдрдің биіктігі h-қа тең. Толық бетінің ауданын табыңыз.
AB=x
SH=h
R-
 ABC-ға сырттай сызылған шеңбердің радиусы
ABC-ға сырттай сызылған шеңбердің радиусы
 R=
R=
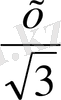
AS 2 =SH 2 +AH 2
X
2
=(
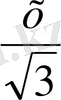
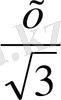 )
2
+h
2
)
2
+h
2
X
2
-
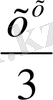 =h
2
=h
2
X
2
=
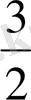 h
2
S
ABC
=
h
2
S
ABC
=
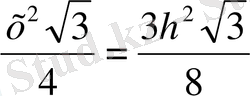
S
т. б
=4
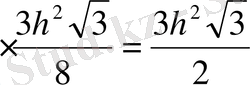
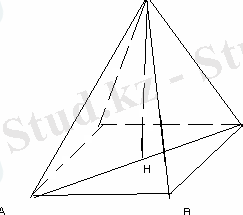
№22 (5 нұсқа №21)
Көлемі 4 см 3 , ал табанының қабырғасы 2 см-ге тең төртбұрышты дұрыс пирамиданың бүйір қырының ұзындығын табыңыз.
 V=4cм
3
V=4cм
3
AB=2 см
S ABCD =2 2 =4см 2
V=
 S
ABCD
*SH
S
ABCD
*SH
SH=3V: S ABCD
SH=12:4=3
АС=2
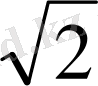 , HC=
, HC=
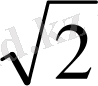
SC=
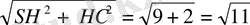
№23. (15 нұсқа №16)
Пирамиданың табан қабырғасы а-ға тең шаршы. Іргелес екі бүйір жағы табынына перпендикуляр, ал басқа екі бүйір жағы табанымен 60 0 бұрыш жасайды. Пирамиданың толық бетінің ауданын табыңыз.
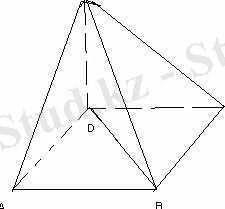
ABCB-шаршы, AB=a
<SAD=<SCD=60 0
S т. б =S таб +2(S ASD +S SAB )
S таб =a 2
SD = tg60 0
AD
SA=
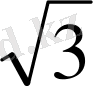 a
a
S
ASB
=
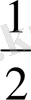 AS*AB=
AS*AB=
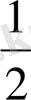 *a*2a=a
2
*a*2a=a
2
S
SAD
=
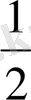 AD*SA=
AD*SA=
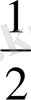 *a*
*a*
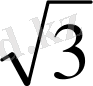 a=
a=
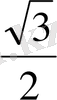 a
2
a
2
S
т. б
=a
2
+2(a
2
+
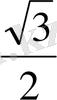 a
2
)
2
=a
2
(3+
a
2
)
2
=a
2
(3+
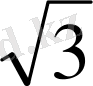 )
)
2006 ж
№24. (14 нұсқа №30)
Пирамиданың табанына параллель жазықтық қимасы биіктікті 1:1 қатынасындай бөледі. Қима ауданы 2 м 2 болса, табан ауданы неге тең?
SH 1 =2SH S 1 =2 м 2
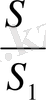 =(
=(
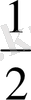 )
2
)
2
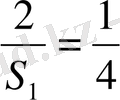
S 1 =8 м 2
№25 (17 нұсқа №13)
MABCD дұрыс төртбұрышты пирамиданың МО биіктігі 7 см-ге тең, ал бүйір қыры 14 см- ге тең болса, онда

 скаляр көбейтіндісін табыңыз.
скаляр көбейтіндісін табыңыз.
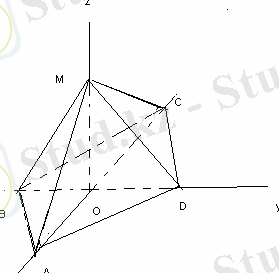
MO=7, MA=14.
AO 2 = MA 2 -MO 2
AO=
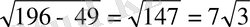
M(0; 0; 7), O(0; 0; 0), C(-7
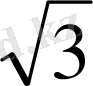 ; 0; 0)
; 0; 0)
MO(0; 0; 7)
MC(-7
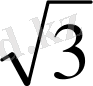 ; 0; 7)
; 0; 7)

 =0+0+49=49
=0+0+49=49
2007 ж
№26 (6 нұсқа №24)
Төртбұрышты дұрыс пирамиданың табан қабырғасы а-ға тең, бүйір қырындағы екі жақты бұрыштары 120 0 -тан. Пирамиданың көлемі неге тең?
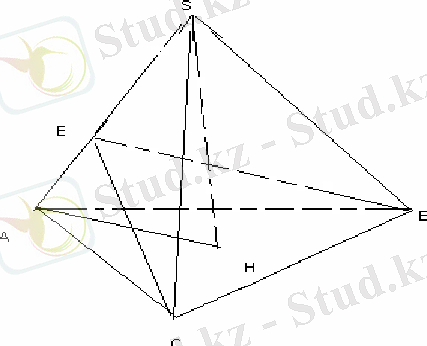 S
таб
=
S
таб
=
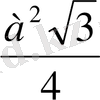
 ABC:
ABC:
CB 2 =CE 2 +EB 2 -2CE *CB cos120 0
CE=x
a 2 =3x 2
x=
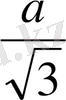
 SAC:
SAC:
AE 2 =AC 2 -CE 2
AE=
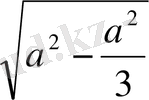 =a
=a
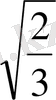
AS=CS=y
ES 2 +EC 2 =SC 2
ES=AS-ES
(y- a
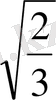 )
2
+
)
2
+
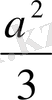 =y
2
=y
2
y
2
-2ax
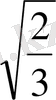 +2
+2
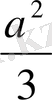 +
+
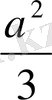 = y
2
= y
2
y=
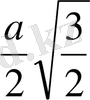
AS=
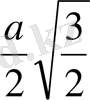
 SAH: AH=
SAH: AH=
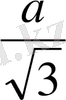
SH 2 =AS 2 -AH 2
SH=
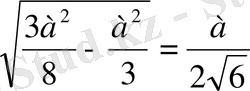
V=
 S
таб
SH=
S
таб
SH=
 *
*
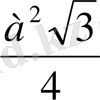 *
*
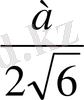 =
=
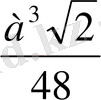
2009 ж
№27 (1 нұсқа №18)
Пирамиданың табаны тік бұрышты үшбұрыш, 30 0 төбесіне қарсы жатқан катеті 30 см. Бүйір қырлары табан жазықтығына 60 0 бұрыш жасаса, пирамиданың биіктігін табыңыз.
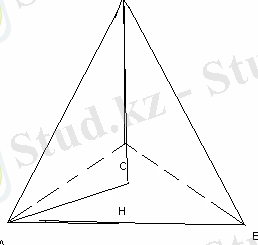
 ABC-тік бұрышты үшбұрыш
ABC-тік бұрышты үшбұрыш
<A=30 0 , BC=30, <SAH=60 0
SH=?
AB=60
AC=
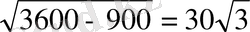
R-
 ABC-ға сырттай сызылған шеңбердің радиусы
ABC-ға сырттай сызылған шеңбердің радиусы
R=AH
R=
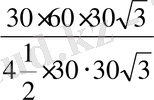 =30
=30
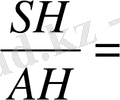 tg60
0
tg60
0
SH=30
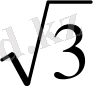
№28 (2 нұсқа № 19)
SABC пирамидасының SB қыры биіктігі болады. BС=18 см, AB= 12 см,
SB=5 см <CBA=90 0 болса, пирамиданың төбесінен табанының медианаларының қиылысу нүктесіне дейінгі қашықтықты табыңыз.
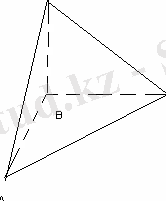 BС=18 см, AB= 12 см, SB=5 см <CBA=90
0
SO-?
BС=18 см, AB= 12 см, SB=5 см <CBA=90
0
SO-?
AC=

m-
 ABC-ның АС-ға жүргізілген медианасы
ABC-ның АС-ға жүргізілген медианасы
m=
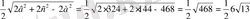
BO-
 АВС-ның медианаларының қиылысу нүктесі
АВС-ның медианаларының қиылысу нүктесі
BO=
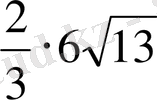 =4
=4
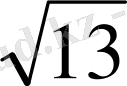
SO 2 =SB 2 +BO 2
SO=
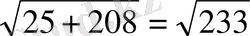
№29 (3 нұсқа №25)
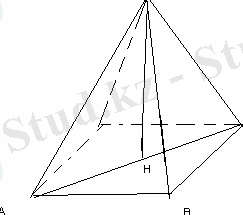 Пирамиданың табаны-параллелограмм, оның қабырғасы 3 см және 7 см, ал диогональдарының бірі 6 см. Пирамиданың биіктігі диогональдарының қиылысу нүктесінен өтеді, ол 4 см-ге тең. Бүйір қырын табыңыз.
Пирамиданың табаны-параллелограмм, оның қабырғасы 3 см және 7 см, ал диогональдарының бірі 6 см. Пирамиданың биіктігі диогональдарының қиылысу нүктесінен өтеді, ол 4 см-ге тең. Бүйір қырын табыңыз.
AB=3, BC=7, AC=6, SH=4
SA-?
AC 2 +BD 2 =2(AB 2 +BC 2 )
BD 2 =2(9+49) -36
BD 2 =80
BD=4
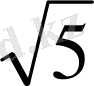
BH=BD:2=2
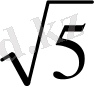
SB 2 =SH 2 +BH 2
SB 2 =16+20=36
SB=6
SA 2 =9+16=25
SA=5
№30 (7 нұсқа №25)
М нүктесі тең түйірлі ABCD трапеция жазықтығынан тысқары жатыр және трапеция төбелерінен бірдей 7 см қашықтықта орналасқан. Егер AB= 12 см, DC= 8 см, AD=6см болса, М нүктесінен трапеция жазықтығына дейінгі қашықтықты табыңыз.
R ABCD =R ABD
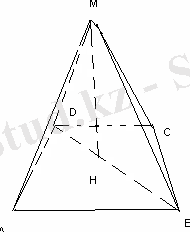
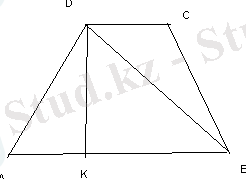
AK=(AB-DC) :2=(12-8) :2=2
DK 2 =AD 2 -AK 2
DK 2 =36-4=32
DK=4
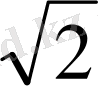
DB
2
=DK
2
+KB
2
KB=AB-AK=12-2=10
DB 2 =32+100=132
DB=2
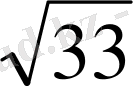
P
ABD
=(12+2
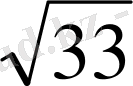 +6) :2=9+
+6) :2=9+
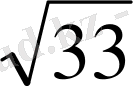
S
ABD
=

R
ABD
=
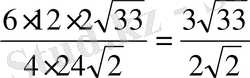
MO=
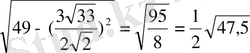
№31 (13 нұсқа №25)
Дұрыс төртбұрышты пирамиданың табанының диогоналі 4
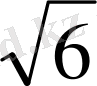 см, бүйір жақтары табан жазықтығымен 60
0
жасайды. Пирамидаға іштей сызылған сфераның бетінің ауданын табыңыз.
см, бүйір жақтары табан жазықтығымен 60
0
жасайды. Пирамидаға іштей сызылған сфераның бетінің ауданын табыңыз.
AC=4
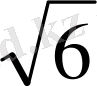
<SHO=60 0
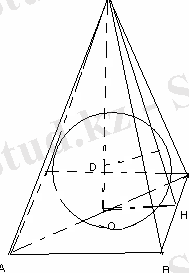 r
cфера
-?
r
cфера
-?
AB 2 +BC 2 =AC 2
2 AB 2 =96
AB 2 =48
AB=4
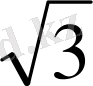
OH=2
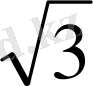
<OSH=30 0
r
cфера
=r tg30
0
=2
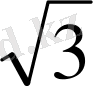 *
*
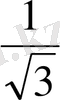 =2
=2
S=4
 r
cфера
2
=4
r
cфера
2
=4
 *2
2
=16
*2
2
=16

№32( 15 нұсқа №24)
Үшбұрышты дұрыс пирамиданың биіктігі мен бүйір жағының арасындағы бұрыш 30 0 -қа тең. Пирамидаға іштей сызылған шардың радиусы 1 см-ге тең болса, табан қабырғасының ұзындығын табыңыз.
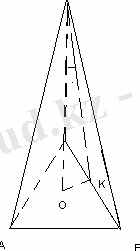 <OSK=30
0
<OSK=30
0
r
ABC
=
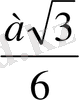
SK=2OK=2
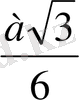 =
=
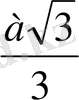
SO=
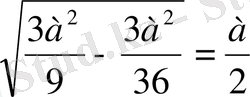
r
cфера
=
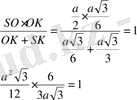
a=6
AB=3
№33 (16 нұсқа №24)
Пирамиданың табанында катеттері 6 см және 8 см болып келетін тік бұрышты үшбұрыш жатады. Пирамиданың табанындағы барлық екі жақты бұрыштар 60 0 -қа тең. Пирамиданың биіктігін табыңыз.
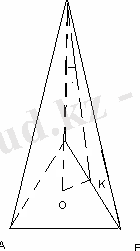 AC=6, BC=8, AC=10
AC=6, BC=8, AC=10
OK=(6+8-10) /2=2
<OSK=30 0
SK=2OK=4
SO 2 =SK 2 -OK 2
SO 2 =16-4=12
SO=2
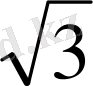
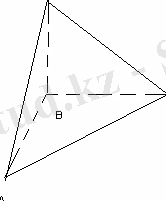
№34 (25 нұсқа №25)
Үшбұрышты пирамиданың екі бүйір жағы өзара перпендикуляр және олардың аудандары P мен Q -ға тең, ал ортақ қырының ұзындығы а-ға тең. Пирамиданың көлемі неге тең?
S ASB =P, S BSC =Q, SB=a V-?
AB=x, BC=y
 S
ASB
=
S
ASB
=
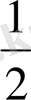 AB SB
AB SB
x=2P:a
S
BSC
=
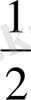 BC* SB
BC* SB
y=2Q:a
S
ABC
=
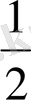 AB* BC=
AB* BC=
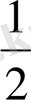
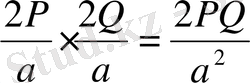
V=
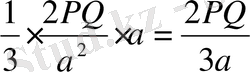
2010 ж
№35 (9 нұсқа №24)
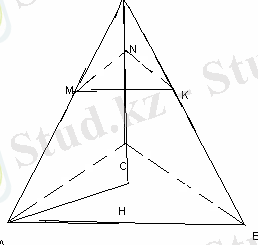
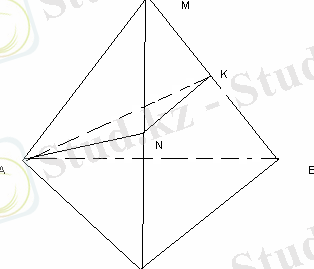 МАВС пирамидасының барлық қырлары 6 см-ге тең, ВМ кесіндісінің ортасы К және А нүктелері арқылы және ВС қырына параллель өтетін қиманың периметрін табыңыз.
МАВС пирамидасының барлық қырлары 6 см-ге тең, ВМ кесіндісінің ортасы К және А нүктелері арқылы және ВС қырына параллель өтетін қиманың периметрін табыңыз.
AK 2 =AB 2 -BK 2
AK 2 =36-9=27
AK=3
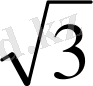
KN=3
AN=3
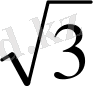
P=3+3
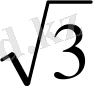 +3
+3
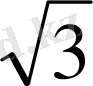 =3(2
=3(2
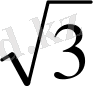 +1)
+1)
№36(15 нұсқа №24)
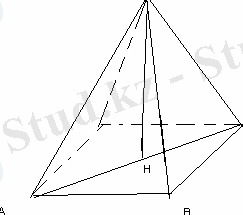 Дұрыс төртбұрышты пирамиданың диогональдық қимасы табанымен тең шамалы. Егер бүйір қыры 5 см-ге тең болса, пирамиданың табанының ауданын табыңыз.
Дұрыс төртбұрышты пирамиданың диогональдық қимасы табанымен тең шамалы. Егер бүйір қыры 5 см-ге тең болса, пирамиданың табанының ауданын табыңыз.
S ASC =S таб
AS=5, S таб -?
SH=h
AB=x
AH 2 =AS 2 -SH 2 =25-h 2
AC=
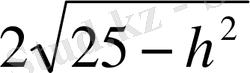
AC 2 =2AB 2
AB 2 =2 (25-h 2 )
S
ASC
=
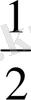 AC *SH S
таб
= AB
2
AC *SH S
таб
= AB
2
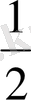
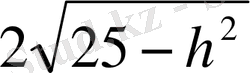 h=2 (25-h
2
)
h=2 (25-h
2
)
h=
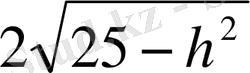
h 2 =4(25-h 2 )
5h 2 =100
h 2 =20
h=2
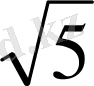
AB 2 =2(25-20) =10
S таб =10
№37 (5 нұсқа №29)
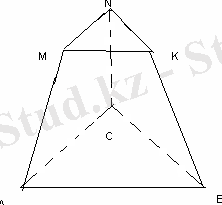 Табанының қабырғалары 3 м және 2 м болатын, ал бүйір бетінің ауданы табандарының қосындысымен тең шамалы болатын дұрыс қиық пирамиданың көлемін табыңыз.
Табанының қабырғалары 3 м және 2 м болатын, ал бүйір бетінің ауданы табандарының қосындысымен тең шамалы болатын дұрыс қиық пирамиданың көлемін табыңыз.
AB=AC=BC=3
MN=NK=MK=2
S б. б = S ABC + S MNK
V-?
R
ABC
=
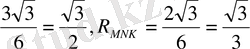
S
таб
=
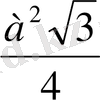
S
ABC
=
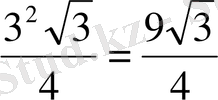
S
MNK
=
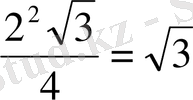
S
б. б
=
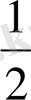 (P
ABC
+P
MNK
) m, m-бүйір жағының апофемасы
(P
ABC
+P
MNK
) m, m-бүйір жағының апофемасы
S
б. б
=
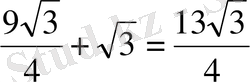
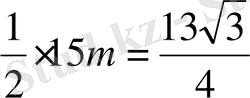
m=
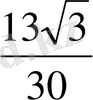
R
ABC
-R
MNK
=
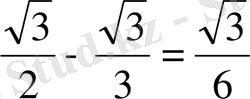
H
пир
=
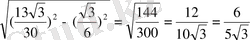
V=
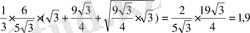
№38 (16 нұсқа №29)
Табандарының ауданы 16 см 2 және 4см 2 , ал биіктігі 3 см-гетең қиық пирамиданың көлемін табыңыз.
S ABC =16 см 2
S MNK =4см 2
H=3 см
V-?
V=
 3 (16+4+
3 (16+4+
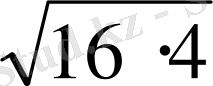 ) =28 см
3
) =28 см
3
№39 (17 нұсқа №24)
Үшбұрышты қиық пирамиданың биіктігі 10 м-ге тең, ал табандарының қабырғалары 27 м, 29 м, 52 м-ге тең және екінші табанының периметрі 72 м-ге тең. Пирамиданың көлемін табыңыз.
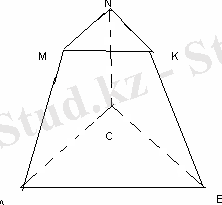 H=10 м, AC=27, BC=29, AB=52
H=10 м, AC=27, BC=29, AB=52
P MNK =72, V-?
P ABC =24+29+52=108
S
ABC
=
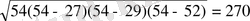
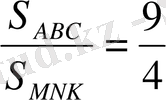
S MNK =120
V=
 *10 *(270+120+
*10 *(270+120+
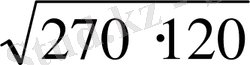 ) =1900м
2
) =1900м
2
ІІІ бөлім Параллелепипед.
Параллелепипед -барлық жақтары параллелограммдар болатын призма.
Тік параллелепипед- бүйір қырлары табанына перпендикуляр параллелепипед.
а, в, с- қабырғалары, d-диогональ
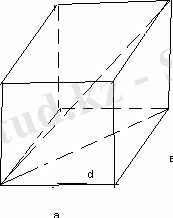
Тік параллелепипедтің барлық жақтары -тік төртбұрыштар.
V=abc;
S б. б =2c(a+b)
S т. б =2(ab+bc+ac)
d 2 =a 2 +b 2 +c 2
2003 ж
№1 (3 нұсқа №21)
Жақтарының аудандары 6 см 2 , 2см 2 және 3см 2 тең тік бұрышты параллелепипедтің көлемін табыңыз.
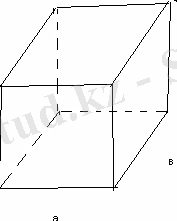 S
1
=ab
S
1
=ab
ab=6 b=6:a
S 2 =ac
ac=2 c=2:a
S 3 =bc
bc= 3
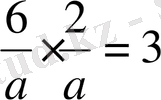
a
2
=4
a=2
b=6:2=3
c=2:2=1
V=abc=6cм 3
№2(8 нұсқа №19)
Биіктігі 4 см-ге тең диагоналі табан жазықтығымен 45 0 бұрыш жасайтын тік бұрышты табаны шаршы параллелепипед берілген. Параллелепипедтің көлемін табыңыз.
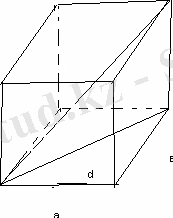
с=4см
d=4cм
а 2 +в 2 =d 2
2a 2 =16
a 2 =8
S таб = a 2
S таб =8
V=8*4=32cм
2
№3 (9 нұсқа №19)
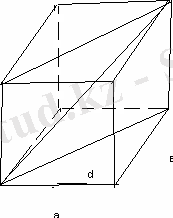 Тік бұрышты параллелепипедтің табан қабырғалары 7 дм және 24 дм, биіктігі 8 дм. Диогональдық қимасының ауданын табыңыз.
Тік бұрышты параллелепипедтің табан қабырғалары 7 дм және 24 дм, биіктігі 8 дм. Диогональдық қимасының ауданын табыңыз.
a=7 дм
b=24дм
c=8 дм
d 2 =a 2 +b 2
d 2 =49+576=625
d=25
S
қима
=25*8=200дм
2
= 2м
2
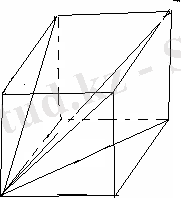
№4. ( 15 нұсқа №21)
Тік бұрышты параллелепипедтің бір төбеден шығатын үш жағының диогональдарының ұзындығы 2
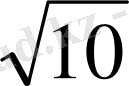 см, 2
см, 2
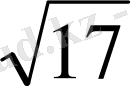 см және 10 см. Параллелепипедтің диогоналін табыңыз.
см және 10 см. Параллелепипедтің диогоналін табыңыз.
d
1
=2
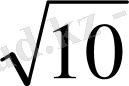 см, d
2
=2
см, d
2
=2
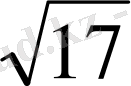 см, d
3
=10 см. d=?
см, d
3
=10 см. d=?
а
2
+в
2
=(2
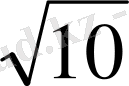 )
2
)
2
a
2
+c
2
=(2
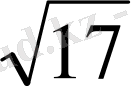 )
2
)
2
в 2 +с 2 =10 2
в 2 =40-а 2
с 2 =68-a 2
40-а 2 +68-a 2 =100
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz