8-сынып: Квадрат теңдеулерді шешу - сабақ жоспары, тапсырмалар және бағалау


8 сынып
Тақырыбы: Квадрат теңдеулерді шешу.
Мақсаты:
- Тақырып бойынша негізгі білім мен біліктілікті жинақтау, қорытындылау
- Логикалық ойлауын, еске сақтауын дамыту;
- Еңбексүйгіштікке, өзара көмекке, бір-бірін сыйлауға тәрбиелеу
Сабақтың жүрісі:
1. Ұйымдастыру
Әрбір балаға нәтижелік карта үлестіріледі. Оны бала толтырады.
2. Ауызша жұмыс. Әрбір дұрыс жауапқа 1 ұпай қояды.
- Екінші дәрежелі теңдеу қалай аталады?
- Квадрат теңдеудің түбірі неге байланысты?
- ХХІ ғасыр қашан басталды?
- D 0- ден үлкен болса, теңдеудің неше түбірі бар?
- Айнымалысы бар теңдік
- Білімді бағалайтын нашар баға?
- Теңдеу шешу дегеніміз не?
- Шаманың жоқтығын көрсететін цифр.
- Бірінші коэффициенті 1 болатын квадрат теңдеу.
- 1 жылда күн неше рет шығады?
- Дискриминанат 0-ден кіші болса, квадрат теңдеудің неше түбірі бар.
3. Тест «Квадрат теңдеудің түрлері»
Толым
сыз
Келтір
ілген
Келтіріл
меген
Биква
драт
Бағалау: Қате жоқ-5ұпай, 1-2 қате-4ұпай, 3-4 қате-3 ұпай, 5-6 қате -2
Оқушылар кілт бойынша бір -бірін тексереді.
4. Өз бетімен жұмыс
А-тобы әр дұрыс жауап 1 ұпай, В тобы әр дұрыс жауап-2 ұпай, С тобы әр дұрыс жауап-3 ұпай.
1-нұсқа
А деңгей
№1 . Әрбір
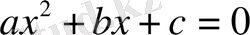 теңдеуі үшін
теңдеуі үшін
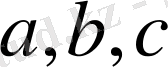 мәндерін ата
мәндерін ата
а)
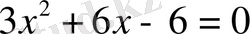 б)
б)
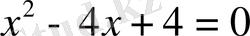
№2 .
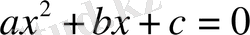 квадрат теңдеуінің дискриминантын
квадрат теңдеуінің дискриминантын
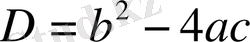 формуласын есептеуді жалғастыр.
формуласын есептеуді жалғастыр.
5х 2 - 7х + 2 = 0, D = b 2 - 4ac = (-7) 2 - 4· 5 · 2 = …;
№3. Теңдеуді шешуді аяқта . 3х 2 - 5х - 2 = 0.
D = b 2 - 4ac = (-5) 2 - 4· 3·(-2) = 49; х 1 = … х 2 =…
В деңгей . Теңдеуді шеш: а) 6х 2 - 4х + 32 = 0; б) х 2 + 5х - 6 = 0.
С деңгей . Теңдеуді шеш:
а) -5х
2
- 4х + 28 = 0; б) 2х
2
-8х-2=0. x
1
=2+
 , x
2
=2-
, x
2
=2-

Қосымша тапсырма. а -ның қандай мәнінде х 2 - 2ах + 3 = 0 теңдеуінің бір түбірі бар болады?
2 нұсқа.
А деңгей
№1. Әрбір ax 2 + bx + c = 0 теңдеуі үшін a, b, c мәнін табыңдар.
а) 4х 2 - 8х + 6 = 0, б) х 2 + 2х - 4 = 0
№2.
№2 .
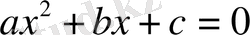 квадрат теңдеуінің дискриминантын
квадрат теңдеуінің дискриминантын
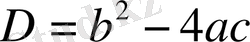 формуласын есептеуді жалғастыр.
формуласын есептеуді жалғастыр.
5х 2 + 8х - 4 = 0, D = b 2 - 4ac = 8 2 - 4· 5 · (- 4) = …;
№3. Теңдеуді шешуді аяқта х 2 - 6х + 5 = 0.
D = b 2 - 4ac = (-6 ) 2 - 4· 1·5 = 16; х 1 = … х 2 =…
В деңгей. Теңдеуді шеш : а) 3х 2 - 2х + 16 = 0; б) 3х 2 - 5х + 2 = 0.
С деңгей . Теңдеуді шешіңдер:
а) 5х
2
+ 4х - 28 = 0; б) х
2
- 6х + 7 = 0; x
1
=3+
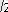 , x
2
=3-
, x
2
=3-
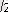 .
.
Қосымша тапсырма. а -ның қандай мәнінде х 2 + 3ах + а = 0 теңдеуінің бір түбірі бар болады?
Бағалау шектері 15 - 20 ұпай - “5”. 9 - 14 ұпай - “4”. 5 - 8 ұпай - “3”.
5. Сабақты қорытындылау
6. Бағалау
А тобы.
№1 . Әрбір
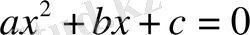 теңдеуі үшін
теңдеуі үшін
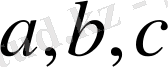 мәндерін ата
мәндерін ата
а)
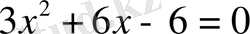 б)
б)
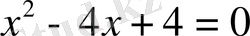
№2 .
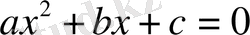 квадрат теңдеуінің дискриминантын
квадрат теңдеуінің дискриминантын
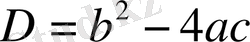 формуласын есептеуді жалғастыр.
формуласын есептеуді жалғастыр.
5х 2 - 7х + 2 = 0, D = b 2 - 4ac = (-7) 2 - 4· 5 · 2 = …;
№3. Теңдеуді шешуді аяқта . 3х 2 - 5х - 2 = 0.
D = b 2 - 4ac = (-5) 2 - 4· 3·(-2) = 49; х 1 = … х 2 =…
В деңгей . Теңдеуді шеш: а) 6х 2 - 4х + 32 = 0; б) х 2 + 5х - 6 = 0.
С деңгей
Теңдеуді шеш: а) -5х
2
- 4х + 28 = 0; б) 2х
2
-8х-2=0. x
1
=2+
 , x
2
=2-
, x
2
=2-

Қосымша тапсырма. а -ның қандай мәнінде х 2 - 2ах + 3 = 0 теңдеуінің бір түбірі бар болады?
2 нұсқа.
А деңгей №1. Әрбір ax 2 + bx + c = 0 теңдеуі үшін a, b, c мәнін табыңдар.
а) 4х 2 - 8х + 6 = 0, б) х 2 + 2х - 4 = 0
№2.
№2 .
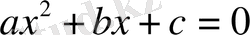 квадрат теңдеуінің дискриминантын
квадрат теңдеуінің дискриминантын
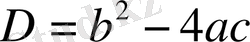 формуласын есептеуді жалғастыр.
формуласын есептеуді жалғастыр.
5х 2 + 8х - 4 = 0, D = b 2 - 4ac = 8 2 - 4· 5 · (- 4) = …;
№3. Теңдеуді шешуді аяқта х 2 - 6х + 5 = 0.
D = b 2 - 4ac = (-6 ) 2 - 4· 1·5 = 16; х 1 = … х 2 =…
В деңгей
Теңдеуді шеш : а) 3х 2 - 2х + 16 = 0; б) 3х 2 - 5х + 2 = 0.
С деңгей
Теңдеуді шешіңдер: а) 5х
2
+ 4х - 28 = 0; б) х
2
- 6х + 7 = 0; x
1
=3+
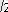 , x
2
=3-
, x
2
=3-
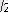 .
.
Қосымша тапсырма. а -ның қандай мәнінде х 2 + 3ах + а = 0 теңдеуінің бір түбірі бар болады?
№1 . Әрбір
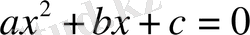 теңдеуі үшін
теңдеуі үшін
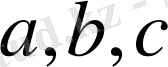 мәндерін ата
мәндерін ата
а)
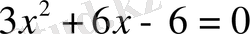 б)
б)
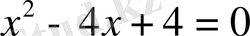
№2 .
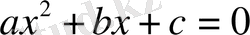 квадрат теңдеуінің дискриминантын
квадрат теңдеуінің дискриминантын
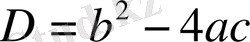 формуласын есептеуді жалғастыр.
формуласын есептеуді жалғастыр.
5х 2 - 7х + 2 = 0, D = b 2 - 4ac = (-7) 2 - 4· 5 · 2 = …;
№3. Теңдеуді шешуді аяқта . 3х 2 - 5х - 2 = 0.
D = b 2 - 4ac = (-5) 2 - 4· 3·(-2) = 49; х 1 = … х 2 =…
В деңгей . Теңдеуді шеш: а) 6х 2 - 4х + 32 = 0; б) х 2 + 5х - 6 = 0.
С деңгей
Теңдеуді шеш: а) -5х
2
- 4х + 28 = 0; б) 2х
2
-8х-2=0. x
1
=2+
 , x
2
=2-
, x
2
=2-

Қосымша тапсырма. а -ның қандай мәнінде х 2 - 2ах + 3 = 0 теңдеуінің бір түбірі бар болады?
2 нұсқа.
А деңгей №1. Әрбір ax 2 + bx + c = 0 теңдеуі үшін a, b, c мәнін табыңдар.
а) 4х 2 - 8х + 6 = 0, б) х 2 + 2х - 4 = 0
№2.
№2 .
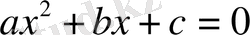 квадрат теңдеуінің дискриминантын
квадрат теңдеуінің дискриминантын
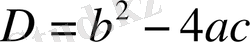 формуласын есептеуді жалғастыр.
формуласын есептеуді жалғастыр.
5х 2 + 8х - 4 = 0, D = b 2 - 4ac = 8 2 - 4· 5 · (- 4) = …;
№3. Теңдеуді шешуді аяқта х 2 - 6х + 5 = 0.
D = b 2 - 4ac = (-6 ) 2 - 4· 1·5 = 16; х 1 = … х 2 =…
В деңгей
Теңдеуді шеш : а) 3х 2 - 2х + 16 = 0; б) 3х 2 - 5х + 2 = 0.
С деңгей
Теңдеуді шешіңдер: а) 5х
2
+ 4х - 28 = 0; б) х
2
- 6х + 7 = 0; x
1
=3+
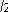 , x
2
=3-
, x
2
=3-
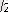 .
.
Қосымша тапсырма. а -ның қандай мәнінде х 2 + 3ах + а = 0 теңдеуінің бір түбірі бар болады?
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz