11-сыныпқа арналған көрсеткіштік теңдеулерді шешу тәсілдері - сабақ жоспары


Сабақтың тақырыбы:
Көрсеткіштік теңдеулерді шешу тәсілдері
Әбу Досмухамбетов атындағы дарынды балаларға мамандандырылған гимназия-интернаты
Петропавловск қаласы.
11 сынып.
Мұғалімі: Четтыкбаева Р. А.
Сабақтың негізгі мақсаты :
Көрсеткіштік теңдеулердің стандартты емес шешу тәсілдерін есептер шығару барысында көрсету
1. Ауызша есептер шығару
Теңдеуді шешіңдер:
1нұсқа
1) 3 х =27
2) 5 х-2 =25
3) ( x =49
4) 2 х+8 = 1/32
5) 6 х-4 =-6
6) 3 х+2 +3 х =90
7) (2/3) х · (3/2) х =1
2нұсқа
- 2х=32
- 6х-3=36
3) (2/3) x =1, 5
4) 5 2х-1 =1/5
5) 9 х-1 =-9
6) 2 х-1 +2 х =6
7) 5 lхl = 5 -1
2. Көрсеткіштік теңдеулерді шешу тәсілдері
1) 4 х+2 -10·3 х ═2 ·3 х+3 -11 ·2 2х
Шешуі
(оқушылар мұғалімнің көмегімен шығарады)
2 2х+4 +11·2 2х = 2·3 х+3 +10·3 х . Дәреженің қасиетімен қолдансақ, аламыз:
2 2х ·2 4 +11·2 2х =2·3 x ·3 3 +10·3 x , онда 16·2 2х +11·2 2х =54 ·3 x +10·3 x ,
27 ·2 2х =64·3 х немесе 3 3 · 4 х =4 3 ·3 х . Теңдеудің екі жақ бөлігін 3 3 ·3 х >0 бөлеміз, онда (4/3) х =(4/3 ) 3 , бұдан х =3.
Жауабы: 3
2) 27 х +12 х ═2·8 х
Шешуі.
Теңдеудің екі жақ бөлігін 8 х >0 бөлеміз. (3/2) 3х + (3/2) х =2,
(3/2) х =у деп белгілейміз, онда у 3 + у -2 =0, (у 3 -1) + (у -1) =0,
(у-1) (у 2 +у+1) + (у -1) =0,
(у -1) (у 2 +у+2) = 0, бұдан у -1 = 0 немесе у 2 +у+2 = 0,
у = 1, D =1-8 = -7<0 шешімі жоқ.
Егер у = 1 болса, онда (3/2) х = 1,
(3/2) х = (3/2) 0 , х = 0.
Жауабы: 0
3. Көрсеткіштік теңдеулерді шешу жасанды әдістері.
Теңдеулерді шешіңдер:
1 мысал. 3 х +4 х ═5 х
Пифагор үштікті еске алып, х=2 түбірін табуға болады.
5 х >0 кез келген х үшін, онда (3/5) х + (4/5) х =1
у= (3/5) х және у=(4/5) х кемімелі функциялар болғандықтан,
у=(3/5) х + (4/5) х кемімелі функция болады. Оның графигі у= 1 түзуімен
бір ғана нүктеде қиылысады. Сондықтан берілген теңдеудің түбірі х=2.
2 мысал.
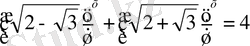
Шешуі.
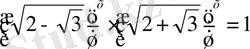 - ге тең екенін байқап,
- ге тең екенін байқап,
жаңа айнымалы еңгіземіз.
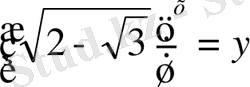 , онда
, онда
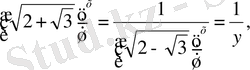
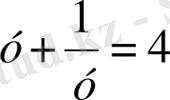 теңдеуді шешеміз. y
2
-4у+1=0,
теңдеуді шешеміз. y
2
-4у+1=0,
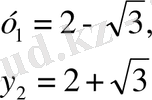
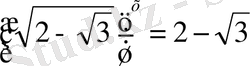 немесе
немесе
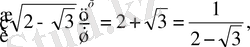
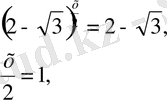
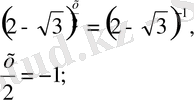
х=2 х= -2
Жауабы: ± 2
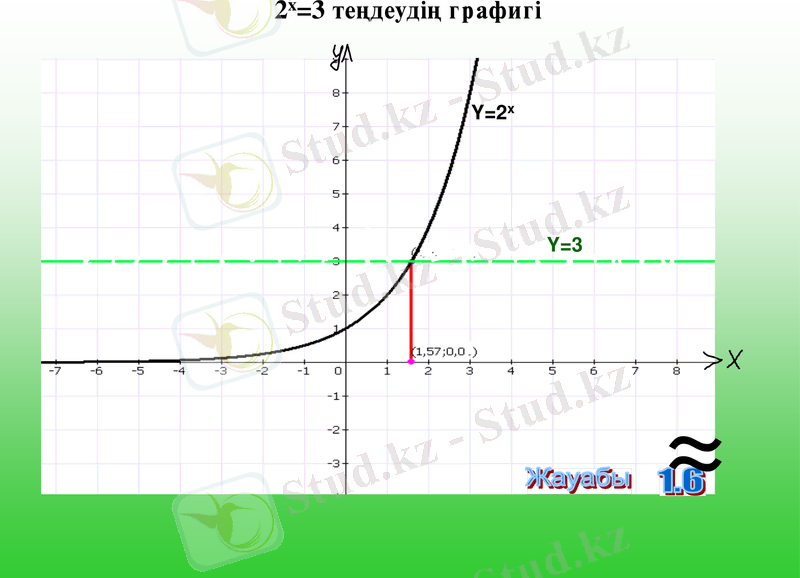
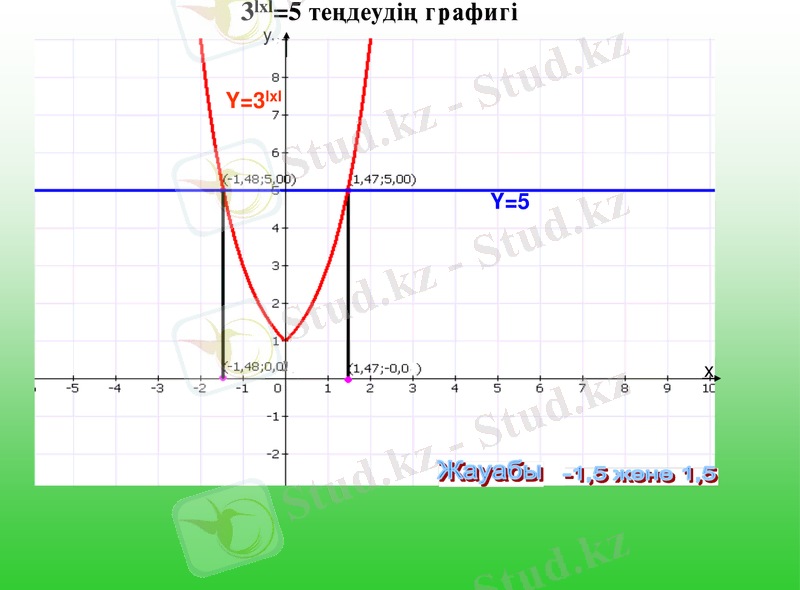
4. Графиктік тәсілі
Шығармашылық тапсырма
Орындаған 11сынып оқушысы Тажібаева Мерей
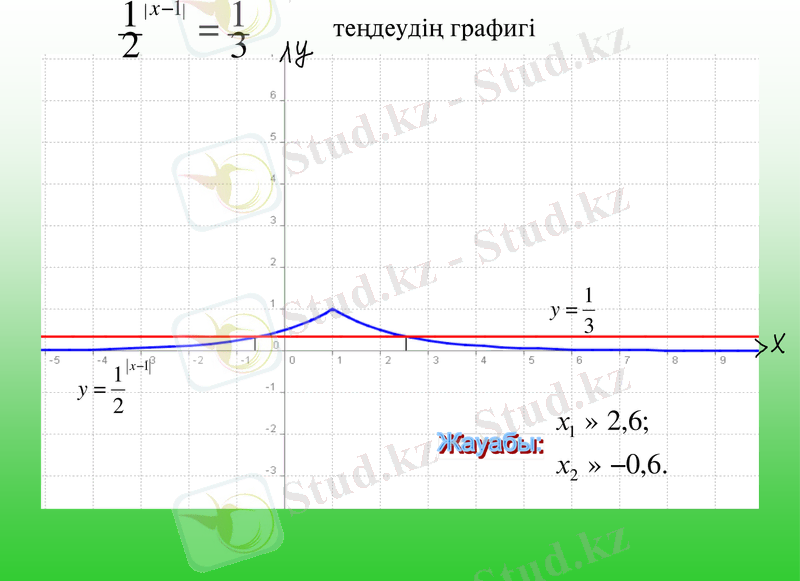
5. Өзіңді тексер:
Теңдеулерді шешіңдер:
- 3·16х+2·81х═5·36хЖауабы: 1; 0, 5
- Жауабы: ± 2
6. Тест
1)
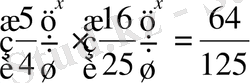 теңдеуінің шешімі
теңдеуінің шешімі
A) 3 B) 2 C) 1 D) 0 E) -1
2)
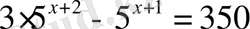 теңдеуінің шешімі
теңдеуінің шешімі
A) 3 B) 2 C) 1 D) 0 E) 5
3)
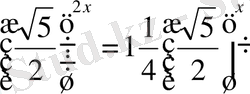 теңдеуінің шешімі
теңдеуінің шешімі
A) 2 B) 3 C) 1 D) 0 E) 0; 2
4)
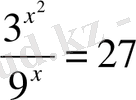 теңдеуінің шешімі
теңдеуінің шешімі
A) 3 B) 3; 1 C) -1 D) 1 E) 3; -1
5)
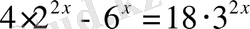 теңдеуінің түбірлері жатқан аралық
теңдеуінің түбірлері жатқан аралық
A)
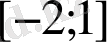 B)
B)
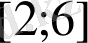 C)
C)
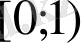 D)
D)
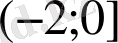 E)
E)
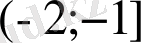
Дұрыс жауаптар:
1А 2С 3А 4Е 5А
Дәптерлерін ауыстырып, оқушылар берілген жауаптарымен салыстырып, бір-бірінің жұмыстарын тексереді.
Сабақтың қорытындысы. Бағалау.
Үйге тапсырма:
№ 206(1), № 209(1, 4), 212(2) және кеспе қағаздағы есептер.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz