Тұтынушы қоржындарын есептеудің оңтайлы әдісі

тұтынушы қоржындарын есептеудің оңтайлы әдісі

Оспанов Дидар, Бисагымова Айнур, 11 сынып

Ғылыми жетекшілері: Сабиханова Гаукар Газезовна математика мұғалімі, Асенова Айжан Оралшаевна информатика мұғалімі

РҚ, ШҚО, Семей қаласы, «№32 ЖОББМ» КММ

Мәселенің өзектілігі:

Ақша табу - бір мәселе, сол ақшаны тиімді жарату - басқа мәселе. Ақшаны табу жаратудан қиын сияқты көрінеді. Шын мәнінде, үйлесімділік болуы керек: ақша таба білу - ұқыпты жаратуға алып келеді. Сол қолда бар капиталдың ұқыпты жұмсау мәселесі - қазіргі таңда өзекті мәселе.

Зерттеу әдістері:

Мектеп қабырғасында үйренген әдіс-тәсілдерімізді біз жобаны жасауда қолдандық. Тұтынушылардан алынған сауалнама нәтижелерінен тұтынушылардың “ойлау көрінісі” анықталды. Анықталған “ойлау көрінісі” формулалар түрінде жазылды. Кейіннен maple11 программалық жүйесі, яғни компьютер арқылы орындадық.

Зерттеудің мақсаты:

Математикалық моделдеу арқылы микроэкономикалық теорияны тереңдетіп зерттеу.

Зерттеудің жаңалығы:

Біз үшін жасаған жоба жаңа! Сатып алуға болатын, тауарларға толы, қоржындарды қағазға түсірп көрдік. Қағазға түсірумен шектеле қоймай, maple11 программалық жүйесінде көрнекті көрсетуге тырыстық.

Алғашқы мағлұматтар

Тұтынушы нарықтық алыс-берiс жасамай тұрып, басты екi мәселенi шешiп алғаны жөн. Мұның бiрiншiсi - өз бюджетiн тиiмдi пайдалану, ал екiншiсi - сол бюджетке сәйкес алынған қоржынның толы әрi тиiмдi болуы. Айтылған екi мәселе де оңай шешiле салатын шаруа емес. Бiраз бас ауыртуға тура келедi. Бiрiншiден, бюджет шектеулi, яғни қалта қарымды емес. Екiншiден, өзіңіз таңдаған қоржынның пайдалық мөлшерi, тиiмдiлiгi жоғары болуы шарт. Онсыз болмайды. Қоржындар әр түрлi болған соң, олардың пайдалық мөлшерi де әр қилы болады. Сондықтан, тұтынушы қалтасы көтеретiн әрi пайдалық мөлшерi жоғары қоржынды адаспай табуы керек. Сонда ғана тұтынушы қалтасының қарымына қарай қоржындардың iшiнен пайдалық мөлшерi ең көбiн алады. Қоржындардағы тауарлардың бағасы және мөлшерi белгiлi.

Нарық неден құралады? Тұтынушының түсiнiгi бойынша, нарық оған сатылатын тауарлардан тұрады. Сатылатын тауарлардың бағалары белгiлi және ол бiр саудадан кейiн өзгеруi мүмкiн емес. Сонымен, тұтынушы нарыққа «тесiк қалтамен» келмейтiнi белгiлi. Тұтынушы сатып алған тауарларын қоржынмен алып кетедi. Демек, тұтынушы үшiн нарық - тауар толы әр түрлi қоржындар.

Нарықта тауарлардың саны да, түрi де шексiз. Бiз нарықтағы әр түрлi тауарлардың санын шартты түрде

\[\Lambda{\cal{Y}}\]

деп белгiлейiк және тауарларды нөмiрлеп алайық, яғни:

1-тауар,
2-тауар, тағы сол сияқты

-тауар.

Тауарлардың мөлшерiн сәйкесiнше

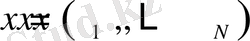
\[\mathcal{X}_{1},\mathcal{X}_{2},\mathcal{X}_{3},\mathcal{X}_{3}\]

деп алайық. Сонда жалпы қоржын былай болады:

Егер

\[{\mathcal{X}}_{1}\]

>0 болса, онда бiрiншi тауар қоржынға тиістi деген сөз. Егер

\[{\mathcal{X}}_{1}\]

=0 болса, онда ол тауар алынған жоқ. Сол сияқты

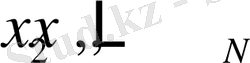оң немесе нөл болуы мүмкiн.

Егер

\[\mathbf{X}\]

-тi тұтыну жиыны деп алсақ, оған қойылатын талаптар мынадай:

Тауарлары болмайтын қоржындар - бос қоржындар. Бос қоржындарды тұтыну жиынына жатқызамыз.

Бiрiншi қоржын:

\[{\mathcal{X}}\ \subseteq\!\left({\mathcal{X}}_{1},\circ*,{\mathcal{X}}_{N}\right)\]

; Екiншi қоржын:

\[{\ y}\,\ {\overline{{=}}}\,\left(\begin{array}{c}{{\!\ y_{1}\!\cdot\!\bullet\!\circ\!\cdot\!\cdot\!\cdot\!\ y}}\end{array}\right)\]

Осыдан құралған аралас қоржындар:

\[z\triangle\tilde{\nu}\frac{1}{2}\left\{\mathrm{\bf~\nu_{1}},1\mathrm{\bf~\nu_{1}~\lambda_{2}~\Delta~\Gamma~}-(\mathrm{\bf~\nabla~\Gamma~\Gamma~\Gamma~\Gamma~\cal~\Delta}\overline{{{\biggr]}}}\right\}\]

және

\[\begin{array}{c c c}{{z\omega\star_{\widetilde{\mathcal{N}}}(~,1,\cdots,1,1.}}&{{-(~~~}}&{{~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~}}\end{array}\]

тағы сол сияқты

\[\mathcal{L}\chi\Re\mathcal{H}\mathcal{H}\mathcal{L}\big(\begin{array}{c c c}{{\mathbf{\Sigma}_{1},\coprod_{\bf i}\parallel_{-}}}&{{\mathcal{N}\big)\quad\big(\qquad\mathcal{O}\qquad\qquad\mathcal{O}\qquad\mathcal{O}\qquad\mathcal{O}\qquad\mathcal{O}\qquad\mathcal{O}\overline{{{\Delta}}}\mathcal{\Delta}\qquad\mathcal{O}\mathcal{O}\overline{{{\Delta}}}\mathcal{\Delta}\mathcal{\bigr)}}}\end{array}\ ,\]

Яғни, бiр тұтыну жиынында қаптарлас жатқан екi қоржынды араластырғанда пайда болған аралас қоржын да тұтыну жиынына кiредi. Демек, араластыру амалын да тұтыну жиынының iшiнен шығармайды.

Тиiмдi қоржынды қалай табуға болады? Ол үшiн

\[\textstyle{\mathcal{X}}^{*}\]

- тиiмдi қоржынды табу жолдарын келтiрейiк.

1-әдiс

\[N=2\]

болған жағдайға арналған.

\[N=2\]

болса

\[\begin{array}{r l}{\operatorname*{max},}&{{}\ u(x_{12}\quad}\end{array}\]

табу қажет, егер
\[\chi_{\bar{1}\bar{2}},\]
келесi шарттарға

\[p_{X M R}y\leq\]

\[0,0\leq\ \mathbf{E}_{12}\]

қанағаттандыратын болса.

Тиiмдi қоржынды табу алгоритмi.

1-қадам. Жазықтықта

\[x_{12}^{*}0\]

координат жүйесiн сызып аламыз.

2-қадам .

\[p_{{\dot{Y}}/k\neq}^{\quad}\to\]

түзуiн жүргiземiз. Ол үшiн

алдымен нүктелердi

\[\bigcup_{\mathbb{Q}\emptyset},\ \ y\]

және

\[\sqrt{_{\underline{{{N}}}\widetilde{\phi}_{1}}}\ ,0\]

белгiлеп аламыз, одан кейiн белгiленген нүктелер арқылы түзу жүргiземiз.

\[A=\bigotimes_{\hat{\mathrm{C}}}^{}\mathbf{,}\quad\underline{{{y}}}\]

нүктесi барлық ақшаға тек екiншi тауар алынғанын сипаттайды.

\[C=\bigcup_{Q\overline{{{\phi}}}}\overline{{{\phi}}}_{1},0\]

нүктесi барлық ақшаға тек бiрiншi тауар алғандығын сипаттайды. Ал жүргiзiлген түзудiң экономикалық мағынасы - қалтада бар қаржыға бағасы сай қоржындарды анықтайды. Сонымен, екiншi қадамда бюджеттiң бәрiн жұмсағанда иелiк ететiн қоржындарды белгiледiк. 1 суретте

\[\ D\]

жиыны - үшбұрыш.

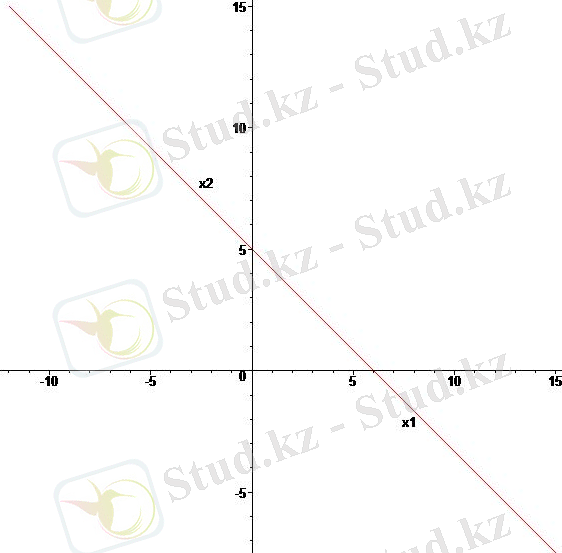
1-сурет. Мүмкiн қоржындар 2-сурет. Деңгей сызығы.

3-қадам.

\[u\hat{c}_{2},\ \ \ \ \ ]=\]

деңгей қисығын сызып аламыз. (2-сурет) . Деңгей қисығын сызу үшiн көбiне дайын программалық жүйелердi (MAPLE, MathCAD) пайдаланады. 2-суретте деңгей қисығы көрсетiлген. Деңгей қисығында жатқан қоржындардың пайдалық мөлшерлерi бiрдей және олар

\[\mathbf{\Sigma}_{\perp}^{\infty}\]

-ке тең. Яғни, деңгей қисығы эквиваленттi қоржындардың сипатын көрсетедi. 2-суретте көрсетiлген деңгей қисығы үшбұрышпен қиылыспайды. Демек, деңгей қисықтың бойындағы қоржындарды қалтамыз көтермейдi.

Сондықтан

\[\mathbf{\Sigma}_{\perp}^{\infty}\]

-тың шамасын бiршама азайту қажет. Ендi

\[\mathbf{\Sigma}_{\perp}^{\infty}\]

-тi екi есе кiшiрейтiп, былайша

\[w(x_{\vec{x}},\quad\ )=\frac{1}{2}\]

қайтадан жаңа деңгей қисығын сызамыз. 3-суретте деңгей қисығы ұйғарым жиынымен қиылысады. Мұндай жағдайда пайдалық мөлшерлерi

\[\frac{\mathbf{S}}{\mathbf{\Lambda}\cdot\sum}\]

-ге тең болатын кейбiр қоржындарға ақшамыз жетедi. Алайда, шамамыз шектеулi, бәрiне бiрдей ақша жетпейдi. Деңгей қисықтың үшбұрыштың iшiнде жатқан бөлiгiне ақшамыз жетедi. Олардың пайдалық мөлшерлерi бiрдей болғанымен бағалары әр түрлi. Мысалы,

\[{\boldsymbol{A}}{\boldsymbol{C}}\]

кесiндiсiн қиятын нүктелерге сәйкес келетiн қоржындардың бағасы

\[\ y\]

тең. Ал үшбұрыштың iшiнде жатқан қоржындар одан арзан.

Ұқсас жұмыстар

Unicode және ASCII символдарын кодтау кестесін салыстыру

Квадрат теңсіздіктер

Экономикадағы тұтынушы

Отбасының қоғамдағы маңыздылығын бағалау

Ұбтға дайындық математика

HTML негіздері, мәтіндерді өңдеу

Қасиетті жеті