Квадрат теңдеулерді қайталау және Виет теоремасын қолдану


Қарағанды қаласы №27 жалпы білім беретін орта мектебінің математика пәні мұғалімі Жакенова А. Ж.
Сабақтын тақырыбы: Квадрат теңдеулерге қайталап есеп шығару. Виет теоремасы
Сабақтын мақсаты:
- Квадрат теңдеулер түбірінің формуласын қайталау.
- Квадрат теңдеулердің дербес жағдайларын шешу.
- Виет теоремасын қолдана білу. .
- Квадрат теңдеуге келтіретін теңдеулерді шешу.
- Оқушылардың оқылатын деректерге қызығушылық және ынтасын ояту.
- Шығармашылық пен жауапкершілікке тәрбиелеу
- Оқушылардың алған білімдерін жетілдідіру және дамыту.
- Оқушылар білімдерін өздері қортындылап өз ойларын айтуды дамыту
Қурал-жабдық:
- Компьютер.
- Мультимедиялық проектор.
- Экран.
Сабақ жоспары:
(сабақ презентациямен көрсетіледі)
- Ұйымдастыру кезені. .
- Жаттығу.
- Нұсқамен жарысу: «Кім зымыранға тез отырады»
- Математикалық диктант.
- Өздік жұмыс (квадрат теңдеуге келтірілетін теңдеулер)
- Үйге тапсырма.
- Қорытынды.
Сабақ барысы:
1. Ұйымдастыру кезені ( слайд1-2)
2. Жаттығу (слайд 3-7)
2. 1
- 2x2+3x+1 = 0
- -4x2+7x+2 = 0
- 3x2-8x = 0
- x2-6x+9 = 0
- 2x2-7x+5 = 0
Барлық теңдеулер толық түрі ма?
(3)
Келтірілген?( 4)
Қай теңдеулерді ауызша шешуге болады?
(3, 4, 5)

2. 2 : Теңдеулер түбірінің көбейтіндісін және қосындысын табыңдар:
А) x
2
-13x+12 = 0
(13; 12)
Б) x
2
-
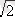 x+6 = 0
(
x+6 = 0
(
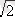 ; 6)
; 6)
В) 3x
2
-10x+3 = 0
(10/3; 1)
Г) 3x
2
-0, 2 = 0
(1/15; 0)
Виет теоремасын тұжырымдау. Квадрат теңдеулердің дербес жағдайларын қайталау.
Виет теоремасын пайдаланып кестені толтырыңдар.
2. 3. Теңдеулердің түбірлерін ойлап көр:
- x2-7x+10 = 0(2; 5)
- x2-1998x+1997 = 0(1; 1997)
- x2-39x-40 = 0(-1; 40)
3. Ойын «Зымыранға кім тез отырады» (слайд 8-9)
Ойын топпен ойналады. Әр топқа келесі тапсырмалар беріледі:
1. Өрнектін мәнін табу:
2. Теңдеуді шешу:
3. Теңдеудің
Тақтаға әр топтан оқушы шығады. Бірінші тапсырманы шығарып, жауабын бірінші сатыға жазады, оларды топтын келесі мушесі шығып шығарады «Кім тез шығарып сатымен зымыранға отырады» сол жеңеді .
Жауаптары:
- Математикалық диктант(слайд 10-11)
1. Бірінші коэффициенті 3( -5), екінші коэффициент і-5( 3), бос мүшесі 0-ге тең квадрат теңдеуді жазыңдар.
2. Екінші коэффициенті және бос мүшесі -2( -3) - ге тең келтірілген квадрат теңдеудің түрін жазыңдар
3. Бірінші коэффициенті -5( -3), бос мүшесі 7( 5) - ке тең толымсыз квадрат теңдеуді жазып, шығарыңдар.
4. Бірінші коэффициенті 3( 5), екінші коэффициенті 5( 7) - ке тең толымсыз квадрат теңдеуді жазып, шығарыңыз.
5. Квадраттық тедеудің түбірлерінің қосындысы мен көбейтіндісі нешеге тең?
X 2 -5x+6=0 ( x2-6x+5=0)
6. b коэффициенті жұп санға тең формуласын қолданып, теңдеуді шеш
3x 2 -8x-3=0 ( 2x2-3x-2=0)
- Қай жағдайда квадрат теңдеуде тек қана бір түбірі болады ?
(Қай жағдайда квадрат теңдеуде түбірі болмайды ? )
Жауаптары :
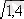 x
2
= -
x
2
= -
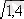
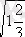 x
2
= -
x
2
= -
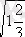



Екі оқушы тақтада шығарады, ал қалғандары дәптерге шығарып жазады. Жауабын компьютермен тексереміз
5. Келтірілген теңдеулер
(слайд 12-13)
(биквадрат теңдеуді қайталау)
Өздік жұмыс.


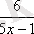 = 3x+2
= 3x+2
Өздік жұмыстын жауаптары:

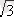 ; -
; -
 ;
;
 ;
;
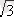
6. Үйге тапсырма (слайд 14)
7. Қорытынды, баға қою.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz