Инверсия және шеңберлер шоғы

Инверсия және оның қолданылуы

Кіріспе . . . 3

1. Инверсия және шеңберлер шоғы . . . 4

1. 1 Жазықтықтың қарапайым түрлендірілулері . . . 4

1. 2 Стереографиялық проекция. Жазықтықтың шексіз алыстағы нүктесі . . . 9

1. 3 Инверсия . . . 12

1. 4 Инверсия қасиеттері . . . 14

1. 5 Шеңберге қатысты нүктенің дәрежесі. Екі шеңбердің радикалдық осі . . . 21

1. 6 Инверсияны салу есептерін шешуде қолдану . . . 26

1. 7 Шеңберлер шоғы . . . 33

1. 8 Эллипстік шоқтың құрылымы . . . 41

1. 9 Параболалық шоқтың құрылымы . . . 42

1. 10 Гиперболалық шоқтың құрылымы . . . 43

1. 11 Птолемей теоремасы . . . 44

2. Комплекс сандар және инверсия . . . 49

2. 1 Комплекс сандардың геометриялық кескіні және оларға қолданылатын амалдар . . . 49

2. 2 Комплекс айнымалының сызықтық функциясы және жазықтықтың қарапайым түрлендірілулері . . . 53

2. 3 Комплекс айнымалының бөлшек-сызықтық функциясы және жазықтықтың нүктелік түрлендірілулері . . . 54

Мысалдар . . . 58

Кіріспе

Тақырыптың өзектілігі: Геометрия есептерін шешудің бірнеше әдісі бар. Солардың бірі-түрлендірулер әдісі. Планиметрия есептерін алгебралық әдіспен шешуге қарағанда түрлендірулерді қолданып шешу әлде қайда қысқа болып табылады. Оқушыларға бір есепті бірнеше әдіспен шешіп көрсету олардың математикаға қызығушылығын арттырады, ойлау қабілетін дамытады. Геометриялық есепті түрлендірулер әдісімен шешу оңай болмайды. Берілген есеп үшін қандай түрлендіру пайдаланатынын тағайындап алу керек. Ал есепті инверсияны пайдаланып шешу шағын шығармышылық жұмыс.

Тақырыптың мақсат-міндеттері: Инверсия түрлендіруі туралы теориялық материалдар жинақтау және оны есептер шешуде қолдануын көрсету.

Геометрияда фигуралардың әр түрлі түрлендірулері маңызды орын алады. Мектепте қозғалыс гомотетия және ұқсас түрлендірулер, сондай-ақ олардың қолданылуы оқылады. Бұл түрлендірулердің маңызды ерекшелігі қарапайым геометриялық образдардың табиғатын сақтайды. Мысалы түзуді түзуге, шеңберді шеңберге түрлендіреді. Ал инверсия бұл түрлендірулерге қарағанда күрделі түрлендіру болып табылады. Инверсияда түзу шеңберге, шеңбер түзуге түрленеді. Түрлендірудің мұндай ерекшелігі элементарлы геометрия есептеріне қолданғанда өзіне тән оқу әдістемесін енгізуді талап етеді. Бұл, ең алдымен, салу есептері мен шеңберлер шоғы теориясына қатысты.

Элементар геометрияның инверсияны қолданбайтын бөлімдерін қарастыру есептердің әркелкілігінде және көп жағдайда жеке ерекшелігі бар жасанды салуларды қолдануына байланысты.

Инверсияның айтылған қолдануларымен қатар ол элементар геометрияның басқа да мәселелерінде және жоғары геометрияда қолданылады.

Дипломдық жұмыста инверсия деп аталатын түрлендіру жан-жақты қарастырылады. Инверсия түрлендіруін салу есептерінде және дәлелдеулерде қолдану басқа жолмен қиын шешілетін бірқатар есептерді шешуді жеңілдетеді.

Бұл әдіс алғаш XIX-ғасырдың 30-шы жылдарында енгізіле бастады. Бұл жұмыста қарастырылатын есептерді шығару әдісін инверсия әдісі, немесе кері радиустар әдісі, немесе айналдыру әдісі деп атауға болады.

Салу есептері оқушының математикалық мәдениетін, дағдысын, ой-өрісін, дайындығын дамытуға зор көмек береді. Инверсия салу есептерін шешуге қолданылатын әдістердің ішінде ең кереметі.

Жазықтықтың қарапайым түрлендірілулері

Бұл тақырыпта жазықтықтағы фигуралар жайында және бір геометриялық фигураны екінші бір геометриялық фигураға түрлендіру басты сөз болады. Қандайда бір жазықтықты қарастырайық және осы жазықтықтың әрбір Х нүктесіне оның $x'$ нүктесі сәйкес қойылатындай заң берілген болсын. Осы заңдылықты жазықтықтың түрлендірілуі , ал $X'$ нүктесі $X$ нүктесінің бейнесі деп аталады. Жазықтықтың түрлендірілуін гректің $\varphi$ әрпімен белгілейік, ал $X'$ нүктесін $\varphi(X)$ деп белгілеп алайық.

Айталық жазықтықта $\varphi$ түрлендірілуі берілсін және $\ F$ сол жазықтықтағы қандайда бір фигура болсын. $\varphi$ түрлендірілуі $F$ фигурасының әрбір $X$ нүктесін оның бейнесі $X'$ нүктесіне көшіреді. $F$ фигурасының нүктелерінің барлық бейнелерінің жиынын $F'$ фигурасы делік. $F'$ фигурасы $F$ фигурасының $\varphi$ түрлендіруіне қатысты бейнесі деп аталады. $F'$ фигурасын $\varphi(F)$ түрінде белгілеуге болады. Бұдан $F' = \varphi(F)$ , яғни $\varphi$ түрлендіруі жазықтықтың әрбір F фигурасын оның бейнесі $F'$ фигурасына көшіріп отырады(1-сурет) .

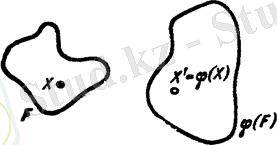
1-сурет

Жалпы жағдайданүкте мен оның бейнесі әртүрлі нүктелер. $X$ нүктесі мен оның бейнесі- $\varphi(X)$ беттессе $X$ нүктесі 𝜑 нүктесі деп аталады. Жазықтықтың әрбір нүктесі $\varphi$ түрлендіруінің қозғалмайтын нүктесі болса, оны теңбе-тең түрлендіру деп атайды. Жазықтықтың тепе-теңдік түрлендірілуін гректің $\varepsilon$ әріпімен белгілейміз. Айталық жазықтықта қандай да бір $\varphi$ түрлендірілуі берілсін. Егер $F$ фигурасы өзінің бейнесі $F'$ -пен беттессе, яғни $F = \varphi(F)$ болса, онда Fфигурасы 𝜑 түрлендірілуіне қатыстыинвариант фигура деп аталады. Қандайда бір түрлендірілуге қатысты инвариант фигураның ешқандай қозғалмайтын нүктесі болмауы мүмкін. Шынында да, егер $\varphi\ \ O$ нүктесінің айналасындағы жазықтықтың айналуы болса, онда жазықтықтың $O$ нүктесінен басқа барлық нүктелері жаңа жағдайға көшеді. Центрі $O$ болатын центрлес шеңберлер жиынтығы қозғалмайтын нүктесі жоқ $\varphi$ түрлендірілуінің инвариант сызықтарының жиынтығы бола алады(2-сурет) .

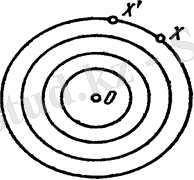
2-сурет

Жазықтықтың қарапайым түрлендірілулерін қарастырайық.

Түзуге қатысты симметрия

Жазықтықтан қандайда бір $L$ түзуін белгілеп аламыз. Егер $X$ нүктесі $L$ түзуінде жатса, онда $\ X$ нүктесіне өзі сәйкес қойылады. Егер $X$ нүктесi $L$ түзуінде жатпаса, онда оның бейнесі ретінде $L$ түзуіне қатысты $\ X$ -ке симметриялы $X'$ нүктесі алынады (3-сурет) .

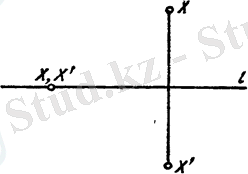
3-сурет

$L$ түзуіне қатысты симметрияда инвариант фигуралар: біріншіден $L$ түзуінің өзі, екіншіден симметрия осі осы түзу болатын барлық фигуралар болады. Түзуге қатысты симметрияның инвариант қозғалмайтын нүктелері $L$ түзуінің барлық нүктелері болып табылады. 4-суретте бірнеше инвариант фигуралар салынған.

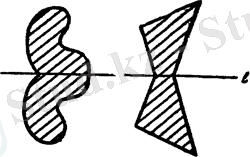
4-сурет

2. Паралель көшіру

Кейбір $\overrightarrow{АВ}$ векторы және $X$ нүктесі берілсін. $\overrightarrow{АВ}$ векторын $X$ нүктесінен бастап салсақ, $XX' = \overrightarrow{АВ}$ болатындай $X'$ нүктесін аламыз. Жазықтықтың әрбір $\ X$ нүктесіне осындай $X'$ нүктесін сәйкес қоятын түрлендіруді жазықтықты паралель көшіру деп атайды. Егер $\overrightarrow{АВ} = \overrightarrow{0}$ болса, онда паралель көшіру теңбе-тең көшіру болады.

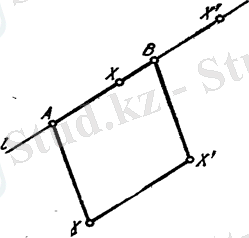
5-сурет 6-сурет

Айталық $\varphi$ - $\overrightarrow{АВ}$ нөлдік векторына паралель көшіру болсын. $\varphi$ түрлендірілуінде қозғалмайтын нүкте жоқ екені көрініп тұр. $\varphi$ түрлендірілуіне қатысты инвариант фигуралар $AB$ түзуіне паралель барлық түзулер болып табылады, мысалы, $AB$ түзуіне паралель барлық түзулер. Басқа да инвариант фигураларды көрсетуге болады. 7 және 8-суреттерде ϕ түрлендірілуіне қатысты $L$ және $Q$ фигуралары көрсетілген. Олардың жекелеген элементтері $\varphi$ түрлендірілуінде $L_{k}$ немесе $Q_{k}$ сәйкесінше $L_{k - 1}$ немесе $Q_{k - 1}$ -дің бейнесі болатындай 7-суретте - . . . , $L_{k - 1}$ , $L_{k}$ , $L_{k + 1}$ , … сызықтарыжәне 8-суретте - . . . , $Q_{k - 1}$ , $Q_{k}$ , $Q_{k + 1}$ , … фигуралары болады.

7-сурет 8-сурет

3. Бүру

Жазықтықта қандайда бір $O$ нүктесін белгілеп алайық, $L$ - осы жазықтықтың кез келген нүктесі болсын. $OX$ кесіндісін $O$ нүктесін айналдыра қандайда бір тұрақты α бұрышына бұрамыз(егер $\alpha > 0$ болса, онда сағат тіліне қарсы бұрамыз, егер α<0 болса, онда сағат тілімен бағыттас бұрамыз) , онда $X$ нүктесі жаңа $X'$ нүктесіне көшеді. Бұл түрлендіруде $OX' = OX$ және $\angle XOX = \alpha$ болатынын көреміз. Жазықтықтың әрбір $X$ нүктесіне осы теңдіктер орындалатындай $X'$ нүктесін сәйкес қоятын түрлендіруді жазықтықты $\alpha$ бұрышына бұру деп атайды. . Егер $\alpha = 0$ болса, онда бұру теңбе-тең түрлендіру болады.

Айталық $\varphi$ - жазықтықты нөлден өзге $\alpha$ бұрышына бұру болсын . Бұруда қозғалмайтын нүкте біреу, ол айналу центрі $O$ нүктесі.

Инвариант фигуралар центрі $O$ болатын шеңберлер және дөңгелектер болады. Егер $\alpha = \frac{2\pi}{n}$ болса, мұндағы $n$ -натурал сан, онда инвариант фигуралар центрі $O$ болатын шеңберге кіретін $m$ -бұрыштар болады. Олардың жақтары $n$ санына еселі болады(9-сурет) . 10-сурет қиындау инвариант фигура бейнеленген.

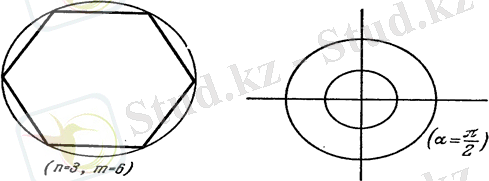
9-сурет 10-сурет

4. Қозғалыс

Қозғалыс деп екі нүктенің ара қашықтығын сақтайтын жазықтықтың түрлендіруін айтамыз. Жоғарыда қарастырылған барлық түрлендірілулер қозғалыс болып табылады.

5. Гомотетия

Жазықтықтан қандайда бір $O$ нүктесін белгілеп алайық. $k > 0$ қандайда бір тұрақты болсын. Центрі $O$ нүктесі коэффициенті $k$ саны гомотетия деп $O$ нүктесін өзіне, ал $O$ нүктесінен өзге кез келген $X$ нүктесін $OX$ сәулесінде жатқан және $OX' = k \bullet OX$ теңдігін қанағаттандыратын $X'$ нүктесіне көшіретін жазықтықтың түрлендіруін айтамыз.

Егер $k = 1$ болса, онда гомотетия теңбе-тең түрлендіру болады. Егер $k \neq 1$ болса, онда бұл түрлендірудің жалғыз қозғалмайтын нүктесі гомотетияның центрі $O$ нүктесі болады. Гомотетияның инвариантфигуралары басы гомотетияның центрі болатын сәулелер болады.

Қиынырақ инвариант фигураларды салудың қарапайым тәсілін көрсетуге болады.

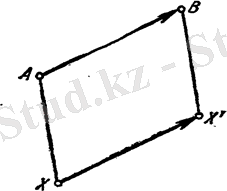
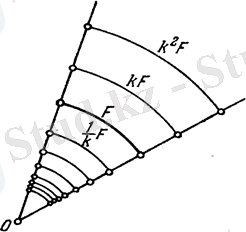
Айталық $F$ - жазықтықтағы қандайда бір фигура (11-сурет) . $mF$ арқылы центрі $O$ нүктесі болатын $m$ коэффициентті гомотетияға қатысты $F$ фигурасының бейнесі $F'$ фигурасын белгілеп аламыз. Центрі $O$ болатын және $k$ коэффициентті гомотетияны $\varphi$ деп белгілеп аламыз. Айталық $F$ -жазықтықтағы қандайда бір фигура.

11-сурет

. . . , $\frac{1}{k^{m}}F$ , $\frac{1}{k^{m - 1}}F$ , …, $\frac{1}{k}F$ , $F, kF, \ldots, k^{m - 1}F, k^{m}F, \ldots$ фигураларын тұрғызайық. Барлық . . . , $\frac{1}{k^{m}}F$ , $\frac{1}{k^{m - 1}}F$ , …, $\frac{1}{k}F$ , $F, kF, \ldots, k^{m - 1}F, k^{m}F, \ldots$ фигураларының бірігуінен тұратын $G$ фигурасы $\varphi$ түрлендірілуіне қатысты инвариант фигура болып табылады(12-сурет) .

12-сурет

Элементар геометрияда маңызды рөл атқаратын тең және ұқсас фигураларға анықтама берейік: егер $F_{1\ }$ фигурасын $F_{2}$ фигурасына көшіретін қозғалыс бар болса, бұл фигуралар тең деп аталады. Егер $F_{1\ }$ фигурасын $F_{2}$ фигурасына көшіретін гомотетия түрлендірілуі бар болса, $F_{1\ }$ және $F_{2}$ фигуралары ұқсас деп аталады.

2. . Жазықтықтың шексіз алыстағы нүктесі

Жоғарыда қарастырылған жазықтық түрлендіруі ұғымыкез келген геометриялық фигураға ауысады. Шынында да анықталған заң бойынша $M$ фигурасының әрбір $X$ нүктесін басқа бір $N$ фигурасының $X'$ нүктесіне сәйкестендіре отырып, $M$ фигурасының $N$ фигурасына $\varphi$ түрлендірілуін аламыз.

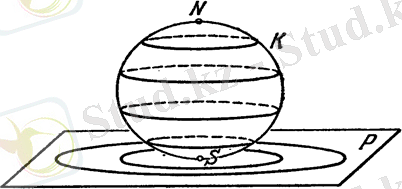
Инверсия түрлендірілуін тереңірек қарастыру үшін арнайы жазықтықтағы сфераның түрлендірілуін қараған жөн. Бұл түрлендірілу стереографиялық проекция деп аталады және келесілерден тұрады: $K$ -сфера, $P$ - $K$ сферасымен $S$ нүктесінде жанасатын жазықтық. $S$ нүктесін $K$ сферасының оңтүстік полюсы деп, ал оған қарама-қарсы жатқан $N$ нүктесін солтүстік полюсы деп атаймыз. Айталық $X$ нүктесі $K$ сферасының $N$ -нан өзге қандайда бір нүктесі. Онда $NX$ сәулесі $P$ жазықтығын қандайда бір $X'$ нүктесінде қияды (13-сурет) .

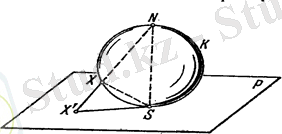
13-сурет

Анықтама: $X$ сферасының $N$ нүктесінен өзге әрбір $X$ нүктесін $P$ жазықтығымен $NX$ сәулесінің қиылысу нүктесі болып табылатын $NX$ нүктесіне көшіру стереографиялық проекция деп аталады. Бұдан $P$ жазықтығы $K$ сферасының $N$ нүктесінен басқа барлық нүктелерінің бейнелерімен түгел жабылатыны көрінді. Сонымен, стереографиялық проекция $K$ сферасын $N$ нүктесінсіз $P$ жазықтығына түрлендіреді.

$K$ сферасында $X$ нүктесі $N$ нүктесіне шексіз жақындағанда, $P$ жазықтығындағы $X$ нүктесінің бейнесі қалай өзгеретінін қарастырайық. $X'NS$ және $XNS$ тікбұрышты үшбұрыштарының ұқсастығынан

$\frac{ХN}{XS} = \frac{NS}{XʹS}$

аламыз.

Бұдан

$X'S = \frac{NS \bullet XS}{NX}$

шығады.

$K$ сферасының радиусын $R$ деп белгілеп алайық. $X$ нүктесі $N$ солтүстік полюсына жеткілікті жақын жатыр, онда $XS > R$ , сондықтан

$XʹS = \frac{2R^{2}}{NX}$

болады.

Бұдан $X$ нүктесі $N(NX - 0)$ нүктесіне шексіз жақындағанда $X'S$ кесіндісінің ұзындығы шексіз өсетіні және $XS$ нүктесі $S$ нүктесінен шексіз алыстайтынын байқаймыз. Олай болса, $N$ нүктесіне сереографикалық проекцияда $P$ жазықтығының ешбір нүктесін сәйкестендіруге болмайды.

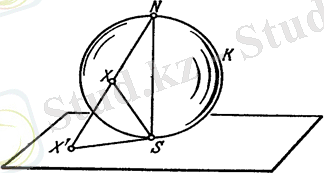
14-сурет

Стереографикалық проекцияда $K$ сферасының барлық нүктелерін қамту, яғни $N$ солтүстік полюсының $P$ жазықтығында бейнесі анықталуы үшін, $P$ жазықтығын жаңа нүктемен толықтыру қажет. $P$ жазықтығының нүктелеріне $О_{\infty}$ жаңа нүктесі қосылады, біз оны шексіз алыстатылған нүкте деп атаймыз. Алдағы тарауларда $P$ жазықтығы $O_{\infty}$ нүктесімен толықтырылған деп есептеледі. Енді $K$ сферасының $N$ солтүстік полюсына $О_{\infty}$ нүктесін сәйкестендіре отырып, стереографикалық проекцияда $N$ сферасының $P$ жазықтығына түрлендіруін аламыз. Шексіз алыстағы нүктенің кейбір қасиеттерін қарастырайық. Айталық, $l'$ - $P$ жазықтығының қандайда бір түзуі болсын. $N$ нүктесі және $l'$ түзуі арқылы жазықтық жүргіземіз (15-сурет) . Бұл жазықтық $K$ сферасын $N$ нүктесінен өтетін қандайда бір $l$ шеңберінің бойында қияды. Стереографикалық проекцияда $l'$ нүктесі $l$ нүктесінің бейнесі болып табылады. Басқа жағынан, $K$ сферасында орналасқан және $N$ нүктесі арқылы өтетін қандайда бір $h$ шеңберінің бейнесі $h$ шеңбері жатқан жазықтық $P$ жазықтығымен түзу бойымен қиылысатын болғандықтан $P$ жазықтығының түзуі болады. Бұдан стереографикалық проекция $K$ сферасының $N$ нүктесі арқылы өтетін барлық шеңберлер жиыны мен $P$ жазықтығының барлық түзулерінің арасында өзара-бірмәнді сәйкестік орнататынын көреміз. Сондықтан, $P$ жазықтығының барлық түзулері стереографикалық проекцияда $N$ нүктесінің образы болып табылатын шексіз алыстағы $О_{\infty}$ нүктесі арқылы өтуі қажет.

Айталық, $l_{1}'$ - $P$ жазықтығына тиісті қандайда бір шеңбер болсын. $K$ сферасының $S$ оңтүстік полюсінен $l_{1}'$ нүктелеріне дейінгі арақашықтық $d + r'$ -тан артық емес болғандықтан, мұндағы $d$ - $S$ нүктесінен $l_{1}'$ шеңберінің центріне дейінгі арақашықтық, ал $r'$ - $l_{1}'$ шеңберінің радиусы, $l_{1}'$ -ке стереографикалық проекцияда көшірілетін, $l'$ сызығы $N$ нүктесі арқылы өтпейді(15-сурет) .

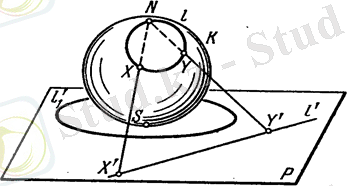
15-сурет

Сондықтан $P$ жазықтығында ешбір шеңбер шексіз аз нүктеден өтетін шеңбер алыстағы $O_{\infty}$ нүктесінен өтпейді. Шеңбердің жазықтықтағы жағдайы бір түзуде жатпайтын үш нүкте арқылы анықталатынын білеміз. Жазықтықтағы түзу жағдайы да үш нүкте арқылы анықталады, оның екі нүктесі кез келген болады, ал үшіншісі міндетті түрде шексіз алыстатылған болады. Сондықтан түзуді шексіз алыстағы нүктеден өтетін шеңбер ретінде қарастыруға болады.

Енді $P$ жазықтығына паралель жазықтықтағы $K$ сферасының барлық шеңберлер үйірін қарастырамыз. Бұл үйірге нөлдік радиусты шеңберлер ретінде $S$ және $N$ нүктелері кіреді деп есептейміз. Стереографикалық проекция бұл шеңберлер үйірін $P$ жазықтығындағы $S$ және шексіз алыстағы нүктені өзіне тиісті ететін және центрі болатын центрлес шеңберлер жиынтығына көшіреді(16-сурет) .

16-сурет

$K$ сферасы мен $P$ жазықтығының жанасу нүктесі ретінде $P$ жазықтығының кез келген нүктесін алуға болатын болғандықтан (бұл үшін $K$ сферасын $P$ жазықтығына паралель орналастыру жеткілікті), кез келген центрлес шеңберлер жүйесіне барлық шеңберлерге ортақ центр және жазықтықтың шексіз алыстағы нүктесі тиісті деп санаймыз.

Инверсия

Айталық жазықтықта центрі $O$ және радиусы $r$ шеңбер берілген болсын. Анықтама: центрі $O$ нүктесі болатын және радиусы $r$ болатын инверсия деп келесі заңмен жазылатын жазықтықтың түрленуін айтамыз: $O$ және $О_{\infty}$ нүктелерінен өзге $X$ нүктесіне $OX' = \frac{r^{2}}{OX}$ теңдігін қанағаттандыратындай $OX$ сәулесіне тиісті $X'$ нүктесі сәйкес қойылады, $O$ нүктесіне шексіз алыстатылған $О_{\infty}$ нүктесі, шексіз алыстатылған $О_{\infty}$ нүктесіне $O$ нүктесі сәйкес қойылады. Жоғарыда берілген центрі $O$ және радиусы r шеңбер инверсия шеңбері деп аталады.

Егер $X$ инверсия шеңберінде жатса, онда $OX = r$ болады, демек $OX' = \frac{r^{2}}{OX}r$ (17-сурет) .

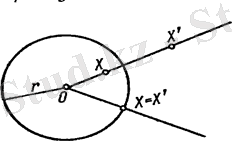
17-сурет

$X$ және $X'$ нүктелері $OX$ сәулесінде жатқандықтан, $X$ және $X'$ нүктелері бір-біріне сәйкес келеді. Бұдан инверсия шеңбері барлық нүктесі қозғалмайтын нүкте екені, ал инверсия шеңберінің инвариант фигура екені шығады. Инверсия шеңберінің ішінде жатқан О-дан өзге $X$ нүктелер инверсия шеңберінің сыртында жатқан нүктелеріне көшіріледі және керісінше инверсия шеңберінңің сыртында жатқан нүктелер осы шеңбердің ішкі нүктелеріне көшіріледі.