Цилиндр призмаға сырттай сызылғандықтан, призманың биіктігі цилиндрдің биіктігіне тең

ҰЛТТЫҚ БІРЫҢҒАЙ ТЕСТІЛЕУДЕГІ СТЕРЕОМЕТРИЯ ЕСЕПТЕРІ

ҰБТ-де стереометрия есептері негізінен пирамидаға, призмаға, конус пен
цилиндрге және түзу мен жазықтық, жазықтық пен жазықтық арасындағы
бұрыштарды, сонымен қатар аудан мен көлемді есептеуге беріледі. Мұндай
есептерді шығару үшін стереометрия формулаларын білумен қатар, сызбаны
дұрыс сала білу керек.
Орта деңгейдегі есептерді шығару-бір-екі стереометриялық фактілер мен
белгілі формулаларды қолданып шығаруға әкеледі. Сондықтан есепті ойымызға
алғаш келген шығару тәсілінен гөрі, азғантай уақыт ойланып, есептің басқа
қарапайым жеңіл әдісін табуға назар аудару керек. Ондай әдіс әрине,
табылады!
Есептің шешімін іздестіруде бағыт-бағдар беруге көмектесетін
планиметрия мен стереометрияға қатысты бірқатар пайдалы фактілерді
тізбектейік және оларды тұжырымдар түрінде берейік.
1-тұжырым. Егер пирамиданың барлық жақтары табан жазықтығына бірдей
бұрыштармен көлбесе, онда пирамиданың биіктігі табанына іштей сызылған
шеңбердің центріне түседі.
1-ескертпе. 1-тұжырымда көрсетілген қасиетке мысалы, дұрыс пирамидалар ие
болады.
2-ескертпе. Егер әу баста пирамиданың табаны-параллелограмм екені белгілі
болса, онда ол ромб болғаны, себебі параллелограммдардың ішінде тек қана
ромбыға ғана іштей шеңбер сызуға болады.
3-ескертпе. Жоғарыда айтылған пирамидалардың барлық апофемалары (бүйір
жағының биіктігі) тең және табанымен бірдей бұрыш жасайды. Дегенмен,
апофемалардың теңдігі барлық жақтары табанымен бірдей бұрышпен көлбейді
дегенді білдіре бермейді.
2-тұжырым. Егер пирамиданың барлық бүйір қырлары тең болса (табанына бірдей
көлбеген), онда оның биіктігі табанына сырттай сызылған шеңбердің центріне
тұрғызылады.
1-ескертпе. 2-тұжырымда көрсетілген қасиет дұрыс пирамидаларға тән.
2-ескертпе. Егер әу баста пирамиданың табаны-параллелограмм екені белгілі
болса, онда ол тіктөртбұрыш болғаны, себебі параллелограммдардың ішінде тек
қана тіктөртбұрышқа ғана сырттай шеңбер сызуға болады.
3-ескертпе. Егер мұндай пирамиданың табаны тік бұрышты үшбұрыш болса, онда
пирамида биіктігі гипотенузаның ортасына түседі және гипотенуза арқылы
өтетін бүйір жағы табанына перпендикуляр болады.
3-тұжырым. Егер тік призмаға сфера іштей сызылса, онда сфераның радиусы
табанына іштей сызылған шеңбердің радиусына тең болады және призма
биіктігінің жартысына тең болады.
4-тұжырым. Егер сфера тік призмаға сырттай сызылса, онда:
1) призма табанына сырттай шеңбер сызуға болады,
2) сфера центрі жоғарғы және төменгі табандарына сырттай сызылған
шеңберлердің центрлерін қосатын кесіндінің ортасында жатады.
1-ескертпе. Сырттай сызылған сфераның радиусын катеттерді призманың
биіктігінің жартысы мен табанына сырттай сызылған шеңбердің радиусы деп
алып, Пифагор теоремасы бойынша табуға болады.
Енді цилиндр мен конусқа байланысты кеңестер берейік.
✓ Көптеген есептерде стереометриялық сызба салу қажет болмайды, тек
қана осьтік қиманы (яғни, конус пен цилиндрдің айналу осі арқылы
өтетін қиманы) қарастыру жеткілікті.
✓ Егер конустың екі жасаушысы тік бұрыш жасайды десе, онда осьтік қима
тік бұрышты үшбұрыш болады.
✓ Конус пен цилиндрдің жанама жазықтықтармен жанасу нүктесіне
жүргізілген перпендикулярлар әрқашан айналу осі арқылы өтеді.

Планиметрия бойынша пайдалы ескертулер. Есептерді шығару кезінде
тіктөртбұрыштың төбесінен диагоналына дейінгі қашықтықты табу есептері жиі
кездеседі.
Есте сақтаңыздар!!! Егер а мен b – тіктөртбұрыштың қабырғалары болса, онда
ізделінді қашықтық мынаған тең: 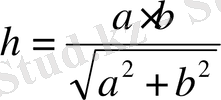. Бұл қашықтықты көбінесе
тіктөртбұрыштың диагоналының жартысымен ауыстырып, қателеседі.

Нені қайталау керек.
Міндетті түрде қайталаңыздар:
✓ Синустар теоремасы мен косинустар теоремасын,
✓ Жарты және қос аргументтің тригонометриялық формулаларын,
✓ Түзу мен жазықтық арасындағы бұрыш пен жазықтықтар арасындағы
сызықтық бұрыштың анықтамасын,
✓ Көлемді есептеу формулаларын,
✓ Үш перпендикуляр туралы теореманы және түзу мен жазықтықтың
перпендикулярлық белгісін.

Есеп шығару мысалдарын қарастырайық.
1-есеп. Дұрыс үшбұрышты пирамиданың биіктігі 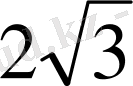, ал бүйір қыры
табанымен 600 бұрыш жасайды. Табан қабырғасына параллель және биіктігі
арқылы өтетін қиманың ауданын табыңтар.
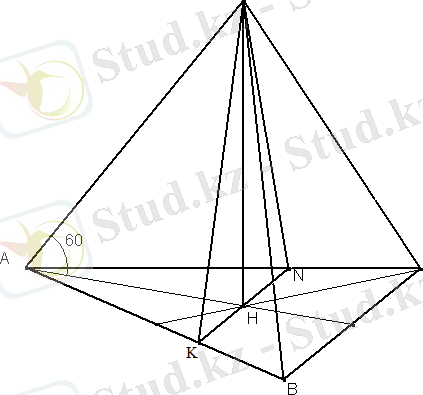Шешуі. 1) Сызбасын саламыз. 2) AKN және ABC үшбұрыштары ұқсас және ұқсастық
коэффициенті кіші үшбұрыш пен үлкен үшбұрыштың медианаларының қатынасына
тең. Ал H нүктесі ABC үшбұрышының медианаларының қиылысу нүктесі болса,
онда 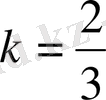. Бұдан 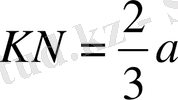, мұндағы a– пирамида табанының қабырғасы.
3) Енді пирамиданың a табан қабырғасын оның биіктігі және бүйір қыры мен
табанының арасындағы бұрыш арқылы өрнектейміз. SHA тік бұрышты үшбұрышынан
AH-ты табамыз: 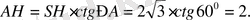AH – ABC үшбұрышының медианасының үштен екі бөлігі
болғандықтан, медиана 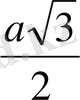-ке тең, онда 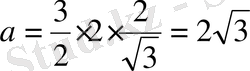, ал 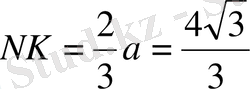. Қиманың ауданын
табайық:
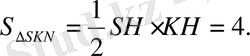
2-есеп. тік призманың табаны-тең бүйірлі тікбұрышты үшбұрыш.
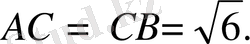ABC1 жазықтығы табан жазықтығымен 600 бұрыш жасайды. Призма көлемін
табыңдар.
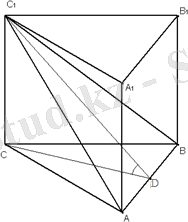Шешуі. 1) Сызба сызамыз. Есеп шартындағы екіжақты бұрыштың сызықтық бұрышы
C1DC бұрышы. Мұндағы D нүктесі–АВ қабырғасының ортасы болады, себебі ,
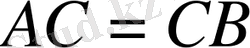онда CD -биіктік. Үш перпендикуляр туралы теорема бойынша C1D мен AB
перпендикуляр.
2) екенін оңай байқауға болады, ал .
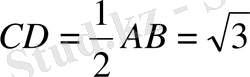3) 600 –тық бұрышы бар C1DC тікбұрышты үшбұрышын қарастыра отырып, CC1-ді
табамыз.
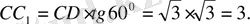
4) Призманың көлемін есептейміз:
.
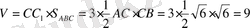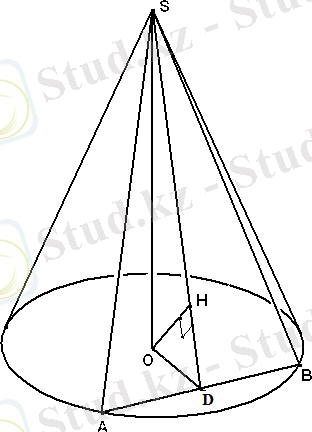
3-есеп. Конустың көлемі 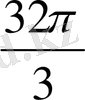, ал табанының радиусы 4-ке тең. Конустың S
төбесі арқылы өтетін жазықтық табанын А және В нүктелерінде қияды. Конус
табанының центрінен қима жазықтыққа дейінгі қашықтық 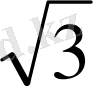-ке тең. SАВ
жазықтығының табан жазықтығымен жасайтын бұрышының градустық өлшемін
табыңдар.
Шешуі. 1) Сызбасын сызамыз. Ең бастысы-қима жазықтығынан табан жазықтығына
дейінгі қашықтықты дұрыс анықтай білу керек. Егер SD кесіндісі SAB
үшбұрышының медианасы болса, онда ОD мен SD АВ-ге перпендикуляр, сондықтан
SOD жазықтығы AB-ге перпендикуляр (түзу мен жазықтықтың
перпендикулярлығының белгісі!!!). Бірақ АВ қима жазықтығында жатқандықтан,
SOD жазықтығы да оған перпендикуляр. О нүктесінен осы жазықтықтардың SD
қиылысу сызығына перпендикуляр түсіру арқылы, біз О нүктесінен қимаға
перпендикуляр тұрғызамыз. Сондықтан .
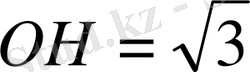2) ODH бұрышын табу керек, оны ( деп белгілейміз. Сонда (OSH=900-(.
3) 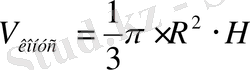, онда конус биіктігі SOH тік бұрышты үшбұрышында:
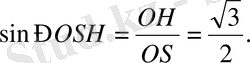Сондықтан берілген бұрыш 600-қа тең, сонда (=300.
4-есеп. KP кесіндісінің ұштары цилиндр табанындағы шеңберлерде жатыр.
Цилиндрдің биіктігі 16-ға, табанының радиусы 10-ға тең, ал KP түзуі мен
табан жазықтығы 450 бұрыш жасайды. Цилиндрдің осінен K және P нүктелері
арқылы өтетін оған параллель жазықтыққа дейінгі қашықтықты табыңдар.
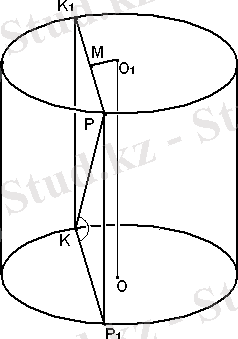Шешуі. 1) Сызба саламыз. Цилиндрдің осі қимаға параллель болғандықтан,
осьтен қимаға дейінгі қашықтық түзудің кез келген нүктесінен жазықтыққа
жүргізілген перпендикулярдың ұзындығына тең. Біздің жағдайымызда О1
нүктесін алу тиімді, онда ізделінді перпендикуляр– О1М кесіндісі, мұндағы М
нүктесі K1P кесіндісінің ортасы.
2) Қима –тіктөртбұрыш, ал диагональ қабырғамен 450 бұрыш жасайды, олай
болса қима– квадрат. Осыған байланысты бізге радиусы 10 болатын шеңбер
центрінен ұзындығы 16–ға тең хордаға дейінгі қашықтықты есептеу керек.
Басқаша айтқанда, есеп O1PK1 теңбүйірлі үшбұрышының биіктігін табуға
тіреледі. Оның 6-ға тең екенін оңай есептеуге болады.
Енді стереометрияның қиын деңгейлі есептері туралы бірер сөз. Бұл
есептер кейбір стереометриялық фактілерді негіздеуді талап етеді, содан
кейін есеп бірнеше стандартты планиметрялық есептерге келеді. ҰБТ-ге
қатысқан оқушылардың көбі мұндай есептерді шығара алмай жүр.
5-есеп. Радиусы 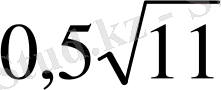болатын шарға дұрыс үшбұрышты призма іштей сызылған.
ВA1 түзуі BСС1 жазықтығымен 450 бұрыш жасайды. Призма көлемін табыңдар.
Шешуі. 1) D1–B1С1 қырының ортасы болсын. Дұрыс призма болғандықтан,
A1D1(B1С1 және A1D1(СС1, содан түзу мен жазықтықтың перпендикулярлық
белгісі бойынша А1D1(ВСС1. Олай болса, (А1ВD – А1В түзуі мен ВСС1
жазықтығының арасындағы бұрыш, яғни (А1ВD = 450.
2) K және K1 – призма табанының центрлері болсын, онда АK = ВK = СK және
А1K = В1K = С1K.
Призма дұрыс болғандықтан, KK1(АВС. Егер О нүктесі KK1 түзуінде жатса, онда
көлбеу мен проекцияның қасиеті бойынша ОА = ОВ = ОС и ОА1 = ОВ1 = ОС1. О
нүктесі-KK1 кесіндісінің ортасы болса, ОKВ және ОK1В1 тікбұрышты
үшбұрыштары екі катеті бойынша тең болады. Олай болса, ОВ = ОВ1. Сол
сияқты, ОА = ОА1 және ОС = ОС1. Бұдан, О нүктесі АВСА1В1С1 призмасының
барлық төбелерінен бірдей қашықтықта орналасқан яғни, оған сырттай сызылған
шардың центрі болады. Есеп шартынан шардың радиусы 0,5, яғни
ОВ = 0,5.
3) АВ = а деп алайық. Сонда . Бірақ (А1D1В тікбұрышты және
(А1ВD = 450. Бұдан, . (ВАА1 үшбұрышынан . , .
Сондықтан (ОK1В1 тікбұрышты үшбұрышынан . Бұдан, . Призма көлемін
мына формула бойынша табамыз: . = , = . Бұдан
.

Стереометриядан тағы бір есепті қарастырайық.
6-есеп. Дұрыс үшбұрышты призмаға сырттай цилиндр сызылған. Цилиндрдің
бүйір бетінің ауданы 14(. Цилиндр осінен призманың бүйір жағының
диагоналына дейінгі қашықтық . Призма көлемін табыңдар.
Шешуі. 1) Цилиндр дұрыс призмасына сырттай сызылғандықтан, оның
табандарының О және О1 центрлері цилиндрдің де табандарының центрлері
болады, ал цилиндрдің радиусы призма табаны–АВС дұрыс үшбұрышына сырттай
сызылған шеңбердің радиусына тең. Дұрыс призма болғандықтан, оның бүйір
қырлары АА1, ВВ1 және СС1 призманың табан жазықтығына перпендикуляр.
Сондықтан ОО1 цилиндр осі АВС жазықтығына перпендикуляр. Бұдан, және
түзу мен жазықтықтың параллельдігінің белгісі бойынша . Айқас
түзулердің ара қашықтығының анықтамасынан ОО1 және СВ1 түзулерінің ара
қашықтығы О нүктесінен ВСС1В1 жағына жүргізілген перпендикулярдың
ұзындығымен тең болады.

2) АК – АВС үшбұрышының биіктігі болсын, онда АК(ВС. Сонда АВС үшбұрышының
центрі АК кесіндісінде жатады. ВВ1(АВС, онда АК(ВВ1. Бұдан, ОК(СВВ1, онда
ОО1 және СВ1 айқас түзулерінің ара қашықтығы призма табанына іштей сызылған
шеңбердің ОК радиусына тең болады. Олай болса, . Призманың кез келген
бүйір жағының кез келген диагоналын қарастыра отырып, осындай нәтиже
аламыз.

3) АВС – дұрыс үшбұрыш. Бұдан, , яғни цилиндрдің R радиусы ОА-ға
тең. Егер Н – цилиндрдің биіктігі болса, оның бүйір бетінің ауданы
. Бұдан . Ары қарай, . Цилиндр призмаға сырттай
сызылғандықтан, призманың биіктігі цилиндрдің биіктігіне тең. Призма
көлемі . Призма табаны- АВС дұрыс үшбұрыш және R –оған сырттай
сызылған шеңбердің радиусы, яғни =36, бұдан призманың
көлемі: .
Жауабы: 63.

Жалиева Айман Алтыбаевна
Совет Одағының Батыры Мәди
Бегенов
атындағы орта мектептің
математика пәнінің мұғалімі
Ақжігіт ауылы
Бейнеу ауданы
Маңғыстау облысы

-----------------------