Квадрат теңсіздік

Капарова Зульфия Буребаевна,
Атырау облысы Исатай ауданы Хамидолла Наубетов
атындағы орта мектептің І санатты математика пәні мұғалімі
Сабақтың тақырыбы: Квадрат теңсіздік.Квадрат теңсіздікті квадраттық
функцияның графигі арқылы шешу.
Сыныбы: 8 сынып
Сабақтың мақсаттары:
Білімділік: Квадрат теңсіздік ұғымымен таныстыру,квадрат теңсіздіктерді
графиктік тәсілмен шешуді үйрету.
Дамытушылық: Ой - өрісін дамыту, ойлау қабілетін арттыру, теориялық
білімін практикада қолдана білу,өз бетімен жұмыс жасай білу дағдысын
қалыптастыру.

Тәрбиелілік: Шапшаңдыққа, іздемпаздыққа, тиянақтылыққа, ұқыптылыққа,
ұжымдық ауызбіршілікке тәрбиелеу.

Сабақтың міндеттері:
• квадраттық функцияның графигін салуды,графиктердің орналасуын,
квадраттық функцияның қасиеттерін қайталау;
• квадраттық функцияның графигін схемалық түрде салу білуін дамытуды
жалғастыру;
• квадраттық теңсіздіктерді шеше білу алгоритмін қалыптастыру;
• квадраттық теңсіздіктерді графиктік тәсілмен шешуге дағдыландыру;
• материалды игеру деңгейін алғашқы тексеру;
• оқушылардың шығармашылық ойлау қабілетін
дамытуға,талдауға,жүйелеуге,өз ойын сауатты жеткізуге ықпал ету;
Оқыту әдістері: проблемалық.
Сабақ типі : аралас сабақ
Сабақ түрі: топтық және ұжымдық
Қажетті құрал –жабдықтар: компьютер,интерактивті тақта.
Сабақтың жүру барысы:
|Сабақтың кезеңдері |Дидактикалық міндеттер |
|1. Сабақтың басталуын |Сабақтың тақырыбы мен міндеттерін хабарлау. |
|ұйымдастыру | |
|2. Теориялық білім мен |Жаңа тақырыпты игеру кезінде қажет болатын |
|практикалық біліктілікті |материалдарды қайталау. |
|қайталау | |
|3. Жаңа материалды игеру. |Квадрат теңсіздіктерді шешу алгоритмін есеп |
| |шығару мысалы арқылы түсіндіре отырып |
| |енгізу. |
|4. Игерілген білімді қолдану |Теңсіздіктерді шешу дағдысын қалыптастыру. |
|5. Сабақты қорытындылау |Сабақтың мақсатқа жетуіне баға беру |

Сабақтың конспектісі:
I. Ұйымдастыру. Оқушыларды түгендеу, сабаққа қатысын тексеру, сабақтың
мақсат -міндетін түсіндіру. (1 Слайд )
II. Негізгі бөлім.
Ι кезең. Үй тапсырмасын тексеру.
Бір оқушы тақтада жұмыс жасайды.Тапсырма: у = х²+х-6 функциясының графигін
салу .Осы уақытта сыныппен фронтальды жұмыс жүреді. (2 Слайд )
Функция графиктерінің кестесі көрсетіледі.
Тапсырма: Берілген функцияны анықтайтын формуланы графикке
сәйкестендіру.
| | |
| | |
| | |

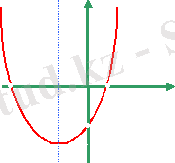
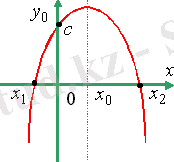
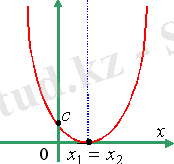
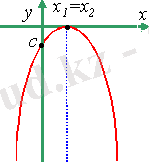
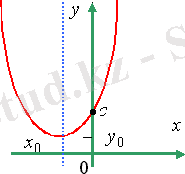
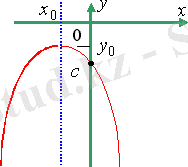
1) у = -х²-3х-3 2) у = х²+4х-5 3) у = х² -2х+1
4) у = х²+5х+ 7 5) у = - х² +2х-1 6) у = - х²+4х+5
- Неден бастау керек?Ең алдымен неге мән береміз? ( Бірінші бағандағы
функциялардың графиктерінің тармағы жоғары бағытталғандықтан,оларға
а коэффициенті оң болатын № 2, 3, 4 формулалар сәйкес.Ал екінші
қатардағы графиктерге № 1, 5, 6 формулалар сәйкес).
- Әрбір бағанмен жеке жұмыс жасаймыз. 1 бағандағы әрбір графикке сәйкес
келетін формула қайсы? ( Бұл графиктердің Ох осімен қиылысу нүктелерінің
саны әртүрлі екенін байқаймыз: а- 2 нүкте, ә- 1 нүкте, б- 0 нүкте. Ал Ох
осімен қиылысу нүктелерінің саны дискриминантқа байланысты.Дискриминант
табамыз. №2: D>0, яғни график- а, №3: D =0, график -ә, қалған №4-б).
- Талдау жүргізудің басқа жолын кім айтады? ( №3- толық квадрат екенін
байқауға болады, D=0, яғни №3-ә. Ал а және б графиктерінің Оу осімен
қиылысу нүктелерінің ординаталарының таңбалары әртүрлі,оны с
коэффициентінен көруге болады.. Олай болса, №2-а, №4-б).
- Екінші ,бағанмен жұмыс жасаймыз.Қай график қай формулаға сәйкес?
( г- №5, сол жағы толық квадрат болғандықтан, в-№6; у>0 , д-№1).
Осы аралықта тақтадағы оқушы у = х²+х-6 функциясының графигін салып
болады.
- Тақтадағы тапсырманы тексерейік .Ескерту бар ма? ( ескерту жоқ).
- Бұл графикті қолданып,жауап беруге болатын қандай сұрақтар қоюға болады?
(осьтермен қиылысу нүктелерінің координаталарын атау,параболаның төбесінің
координаталары,функцияның өсу және кему аралықтары,функцияның ең кіші
мәні ).
ІІ кезең. Жаңа білімді игеру.
-Функцияның графигі бізге көп нәрсе айта алатынын көріп отырмыз.Және бұл
графиктің көмегімен кейбір теңсіздіктерді шешуге болады.Қалай ойлайсыңдар
қандай? (х²+х-6>0; х²+х-6≥0; х²+х-6≤0; х²+х-6<0 ).
-Оны қалай шешуге болады? Мысалы осы графиктің көмегімен х²+х-6>0
теңсіздігін қалай шешуге болады? ( График бойынша функцияның оң мәндерін
анықтаймыз, яғни график Ох осінен х<-3 және х>2 болғанда жоғары
орналасқан ) Жауап графиктен көрсетіледі.

- Ал -3 және 2 теңсіздіктің шешімі бола ала ма? ( Теңсіздік қатаң
болғандықтан ,шешімі бола алмайды.)
- Функция графигінің көмегімен х²+х-6≤0 теңсіздігін шешіңіздер.
(Ох осінен төмен орналасқан графиктің бөлігін
қарастырамыз.Жауап:-3≤х≤2.)
- 3 және 2 санын неге енгіздік? (Теңсіздік қатаң емес болғандықтан.)
- Қазір біз шешкен теңсіздіктер квадрат теңсіздіктер деп аталады.
Анықтама: ах²+bх+с>0 , ах²+bх+с<0, ах²+bх+с≥0 , ах²+bх+с≥0 түріндегі
теңсіздіктер квадрат теңсіздіктер деп аталады.Мұндағы а≠0.
Қалай ойлайсыздар неге олай аталады.?(х-тің еңүлкен дәрежесі 2
болғандықтан.)
- Біз сіздермен квадрат теңсіздікті шешудің тәсілін таптық.Ол қандай?.
(Графиктік.)
-Квадрат теңсіздікті шешу үшін, бізге квадрат функцияның графигін салу
қажет.Ал бұл оңай емес.Мүмкін есеп шығару жолын оңтайландыруға болатын
шығар?Теңсіздікті шешу үшін графикті дәл салу қажет пе?
( Жоқ,бізге тек графиктің Ох осін қиятын
нүктелері ғана маңызды)
-Тағы не маңызды? ( Параболаның тармақтарының бағыты.)
- Олай болса ах²+bх+с >0 квадрат теңсіздігін шешудің алгоритмін құралық.

Оқушылар өз ұсыныстарын айтады және олардың дұрыс,бұрысын айырған соң
дәптерге жазады. (3 Слайд )
1) у= ах²+bх+с функциясын жазамыз .
2) Функцияның нөлдерін табамыз.
3) а санының таңбасына қарап функцияның схемалық графигін саламыз.
4) График бойынша у>0 болатын аралықты анықтаймыз.
III кезең. Теңсіздіктерді шешу дағдысын бекіту.
1) Бір оқушы оқулықтағы №284(1) есебін түсіндіре отырып тақтаға
орындайды.Қалғандары осы есепті дәптерге орындайды.
Теңсіздікті шешіңдер: х²-3х-4<0.
|Тақтадағы жазба |Оқушының ауызшы түсіндірмесі. |
|1) у= х²-3х-4 |Функцияны жазамыз. |
|2) у=0 х²-3х-4=0 |Функцияның нөлдерін табамыз.Ол үшін |
|х= -1 х=4 |теңсіздіктің оң бөлігін 0-ге |
| |теңестіреміз. |
| |Түбірлерін Виет теоремасына сүйеніп |
| |табамыз. |
|3) а > 0 |Ох осінің бойынан -1 және 4 |
| |сандарын белгілейміз. |
| |Бұл нүктелер параболаның Ох осін |
| |қиятын нүктелері.Параболаның |
| |тармағы жоғары бағытталған деп |
| |есептеп схемалық графигін саламыз. |
|Жауап: (-∞; -1 )U (4;+∞) |Бізге функцияның 0-ден үлкен |
| |болатындай х-тің мәндері керек |
| |болғандықтан,графиктің Ох осінен |
| |жоғары бөлігін аламыз. |

2) № 284(3) және №285(1) екі оқушы қатарынан тақтада түсіндірмесіз
орындайды,ал қалған оқушылар өз беттерімен дәптерге орындайды.Болған соң
тексеру,сұрақтарға жауап беру.
3) Бір оқушы тақтада х²-4х+7≤0 теңсіздігін талдап шешеді.
1) у= х²-4х+7
2) у=0 х²-4х+7=0 D= 16-28=-12<0 Түбірі жоқ.
3) а>0
Жауап : Түбірі жоқ
ІV.Сабақты қорытындылау
Бүгінгі сабақта біз, квадрат теңсіздіктермен таныстық және оларды квадрат
функцияның графигі арқылы шешу әдісін үйрендік .Келесі сабақтарда квадрат
теңсіздікті шешудің басқа тәсілін үйренеміз.
- Қандай теңсіздіктерді квадрат теңсіздіктер деп атайды
- Квадрат теңсіздікті шешу алгоритмін еске түсірейік..
Үйге тапсырма : §15; №279,№286
Қосымша : презентация.