Тригонометриялық формулалар мен есептер бойынша сыныптан тыс сайыс жоспары

Автор СЕЙТПАНОВА АЙЗАДА

АҚТӨБЕ ОБЛЫСЫ

ӘЙТЕКЕ БИ АУДАНДЫҚ

ӘДІСТЕМЕЛІК КАБИНЕТ МЕҢГЕРУШІСІ

Жұмыс орнының телефоны: 8(71339) 21680

Сыныптан тыс жұмыс.

Сайыс түрінде өткізілетін сыныптан тыс жұмысқа сынып оқушылары екі топқа бөлініп, топ басшыларын сайлап, өздеріне топ ұранын және төсбелгі ойлап табады. Сайыс төрт кезеңнен тұрады. Барлық тапсырмалар интерактивті тақтада бейнеленеді. Интерактивті тақтада «Алтын кесте» деп аталатын кесте толтырылады және «Формуланы аяқта» бөлімінде формулалар жазылады. Барлық кезең тапсырмаларының дұрыс жауабы бір ұпаймен бағаланады.

Мақсаты :

оқушылардың өтілген тарау бойынша алған білімдерін тексеру; ойлау қабілеттерін дамыту, формулаларды дұрыс пайдалана алуға баулу, өз бетінше жұмыс жасауларын қалыптастыру, пәнге деген қызығушылықтарын арттыру.

Жоспары:

«Формуланы аяқта» (формулалар жазу)
«Білгірлер» (сұрақ жауап)
«Шығарып көр!» (өрнектер мәндерін табу)
«Шешімін тап» (тест)
«Алтын кесте» (кесте толтыру)

Сайыс барысы:

Мұғалімнің кіріспе сөзі. Сайыс жоспары таныстырылады.

«Формуланы аяқта»

Берілген формулаларды толықтырып жазу керек. Әрбір топ өздері таңдаған қалам түсі бойынша формулаларды тақтаға жазады.

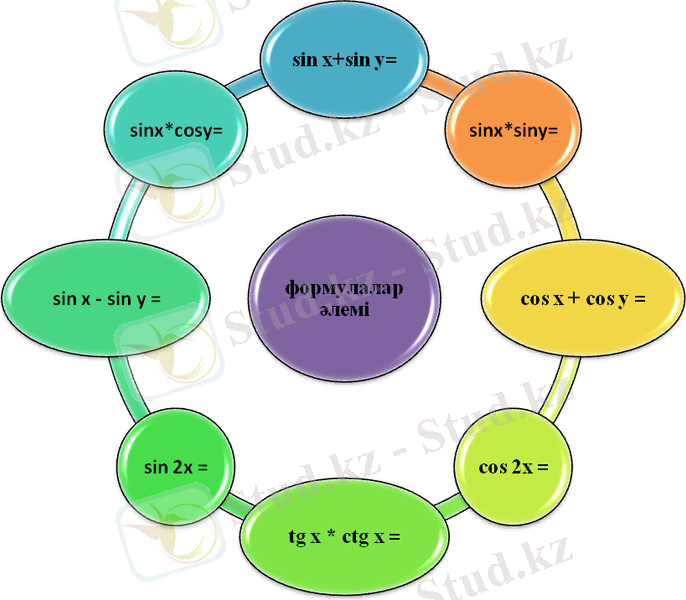
sin x + sin y = 2 sin $\frac{x + y}{2}$ $\frac{x + y}{2}$ cos $\frac{x - y}{2}$ $\frac{x - y}{2}$

sin x*sin y = $\frac{1}{2}$ $\frac{1}{2}$ [cos(x-y) -cos(x+y) ]

cos x + cos y = 2 cos $\frac{x + y}{2}$ $\frac{x + y}{2}$ cos $\frac{x - y}{2}$ $\frac{x - y}{2}$

cos 2x = cos ² x-sin ² x

tg x*ctg x =1

sin 2x =2sinx cosx

sin x - sin y =2 sin $\frac{x - y}{2}$ $\frac{x - y}{2}$ cos $\frac{x + y}{2}$ $\frac{x + y}{2}$

sin x*cos y = $\frac{1}{2}$ $\frac{1}{2}$ [sin(x+y) +sin(x-y) ]

«Білгірлер»

Сұрақтарға жауап беру, әрбір сұраққа жарты минут уақыт беріледі.

Қандай доғаға керілетін бұрышты бір радиан деп атайды? (ұзындығы радиусқа тең доға)
sin х функциясының ең кіші оң периоды неге тен? (2π)
cos x функциясының анықталу облысы?(-∞; +∞)
y=sin х функциясының графигін қалай атайды? (синусоида)
y=arcsin х функциясының мәндер жиыны? ([-π/2; π/2] )
y=tg x функциясы х-тың қандай мәнінде анықталған?(D(y) =(- ∞; π/2+πk) U( π/2+πk; +∞), k∈\in∈\inZ)
у=arсcos х функциясының анықталу облысы?([-1; 1] )
Бірлік шеңбер дегеніміз не?(радиусы 1-ге тең болатын тригонометриялық шеңбер)

«Шығарып көр!»

Берілген өрнектердің мәндерін жылдамдыққа табу қажет.

sin(2 arcsin34\frac{3}{4}34\frac{3}{4}) (37/16\sqrt{7}/167/16\sqrt{7}/16)
sin 2400(-3/2\sqrt{3}/23/2\sqrt{3}/2)
cos (-2100) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \(-3/2\sqrt{3}/23/2\sqrt{3}/2)
cos4π3\frac{4\pi}{3}4π3\frac{4\pi}{3}(-1/2)
cos7π6\frac{7\pi}{6}7π6\frac{7\pi}{6}(-3/2\sqrt{3}/23/2\sqrt{3}/2)
sin 3300(−12) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ ( - \frac{1}{2}) (−12) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ ( - \frac{1}{2})
tg 3000(-3\sqrt{3}3\sqrt{3})
ctg (-2250) (-1)

«ШЕШІМІН ТАП»

Берілген теңдеулердің шешімдерін параққа толтырады. Тапсырманы орындауға 5 минут уақыт.

sin x=1, x=?

πn, n∈Z\pi n, \ n \in Zπn, n∈Z\pi n, \ n \in Z
π+2πn, n∈Z\pi + 2\pi n, \ n \in Zπ+2πn, n∈Z\pi + 2\pi n, \ n \in Z
𝛑𝟐+𝟐𝛑𝐧, 𝐧∈𝐙\frac{\mathbf{\pi}}{\mathbf{2}}\mathbf{+ 2\pi n, \ n \in Z}𝛑𝟐+𝟐𝛑𝐧, 𝐧∈𝐙\frac{\mathbf{\pi}}{\mathbf{2}}\mathbf{+ 2\pi n, \ n \in Z}(*)

cos x=-1, x=?

πn, n∈Z\pi n, \ n \in Zπn, n∈Z\pi n, \ n \in Z
𝛑+𝟐𝛑𝐧, 𝐧∈𝐙\mathbf{\pi + 2\pi n, \ n \in Z}𝛑+𝟐𝛑𝐧, 𝐧∈𝐙\mathbf{\pi + 2\pi n, \ n \in Z}(*)
π2+2πn, n∈Z\frac{\pi}{2} + 2\pi n, \ n \in Zπ2+2πn, n∈Z\frac{\pi}{2} + 2\pi n, \ n \in Z

tg x=0, x=?

𝛑𝐧, 𝐧∈𝐙\mathbf{\pi n, \ n \in Z}𝛑𝐧, 𝐧∈𝐙\mathbf{\pi n, \ n \in Z}(*)
π+2πn, n∈Z\pi + 2\pi n, \ n \in Zπ+2πn, n∈Z\pi + 2\pi n, \ n \in Z
π2+2πn, n∈Z\frac{\pi}{2} + 2\pi n, \ n \in Zπ2+2πn, n∈Z\frac{\pi}{2} + 2\pi n, \ n \in Z

cos x=0, x=?

πn, n∈Z\pi n, \ n \in Zπn, n∈Z\pi n, \ n \in Z
π+2πn, n∈Z\pi + 2\pi n, \ n \in Zπ+2πn, n∈Z\pi + 2\pi n, \ n \in Z
𝛑𝟐+𝟐𝛑𝐧, 𝐧∈𝐙(*) \frac{\mathbf{\pi}}{\mathbf{2}}\mathbf{+ 2\pi n, \ n \in Z\ \ \ \ \ }\mathbf{(*) }𝛑𝟐+𝟐𝛑𝐧, 𝐧∈𝐙(*) \frac{\mathbf{\pi}}{\mathbf{2}}\mathbf{+ 2\pi n, \ n \in Z\ \ \ \ \ }\mathbf{(*) }

ctg x=0, x=?

πn, n∈Z\pi n, \ n \in Zπn, n∈Z\pi n, \ n \in Z
π+2πn, n∈Z\pi + 2\pi n, \ n \in Zπ+2πn, n∈Z\pi + 2\pi n, \ n \in Z
𝛑𝟐+𝟐𝛑𝐧, 𝐧∈𝐙\frac{\mathbf{\pi}}{\mathbf{2}}\mathbf{+ 2\pi n, \ n \in Z}𝛑𝟐+𝟐𝛑𝐧, 𝐧∈𝐙\frac{\mathbf{\pi}}{\mathbf{2}}\mathbf{+ 2\pi n, \ n \in Z}(*)