Келтірілген квадрат теңдеулер

Семей қаласы Т.Ы. Аманов атындағы №16 мектептің
математика пәні мұғалімі Чултуков Нартай Советханұлы

Сабақтың тақырыбы: Теңдеулер әлеміне саяхат. (Слайд №1)

Сабақтың түрі: Ой жарыс, білім сайыс сабағы.
Сабақтың типі: Практикалық сабақ .
Әдіс-тәсілі: Ұжымдық, топтық оқыту.
Сабақтың мақсаты : оқушылардың теңдеулерді шешу тақырыбы бойынша алған
білімдерін жүйелеу.
Сабақтың міндеті:
а) БІЛІМДІЛІК: теңдеулерді шешудің формулалары мен ережелерін өмірде,
математикалық есептеулерде, практикалық іс-әрекеттерде қолдана білу ;
ә) ДАМЫТУШЫЛЫҚ: оқушылардың ойлау, логикалық ойлау қабілеттерін, білік
дағдыларын дамыта отырып, интеллектуалдылығы мен ой ұшқырлығын
қалаптастыру;
б) ТӘРБИЕЛІК: Есеп шешімін іздеу арқылы қиыншылықты жеңуге, ұйымшылдыққа,
дербестікке, дәлдәкке тәрбиелеу.
Сабақтың көрнекілігі: интереактивті тақта, тапсырмалар жазылған парақтар
(слайдтар).
Сабақтың барысы :
1. Ұйымдастыру .
Оқушыларды түгендеу. Топтарға бөлу. Сабақтың мақсатымен және сайыстың
шарттарын қысқаша таныстыру. Оқушылардың назарын сабаққа аудару (слайд
№2).
Үй жұмысын тексеру.
2. Қайталау – білім анасы. Әр топқа қайталауға арналған сұрақтар қою.
І кезең «Нысана» (слайд №6):
• Квадрат теңдеудің анықтамасы;
• Келтірілген квадрат теңдеулер;
• Толық квадрат теңдеу;
• Толымсыз квадрат теңдеу.
Жауаптары: слайд №7.
ІІ кезең «Қорамсақ» (слайд №8):
• Толық квадрат теңдеулерді шешу формулалары (әр формула 1 ұпай);
• Дискриминант сөзінің мағынасы (1 ұпай);
• Толымсыз квадрат теңдеулерді шешу жолдары (әр түрі 1 ұпай);
• Виет теоремасына кері теорема (2 ұпай);
• Рационал теңдедің анықтамасы (1 ұпай);
• Рационал теңдеуді шешу алгоритмі (2 ұпай).
ІІІ кезең «Жебе» (слайд №10): Әр топ қалауы бойынша 7 ғаламаттың біреуін
таңдайды, сол ғаламаттың артында жасырылған тапсырманы топпен орындайды.
• Тадж Махал: 1) -12; -2. 2) -1; 2. 3) -2; 1/3.
• Қытай қорғаны: 1) -13. 2) -6; 4. 3) –1; 1,5.
• Египет пирамидасы: 1) -2; 10/3. 2) -1/3. 3) 3; 4.
• Колизей: 1) -1/2; 4/3. 2) 3/2. 3) 5.
• Дубай: 1) 0. 2) -3. 3) 4/3.
• Мұнара: 1) -2; 10. 2) 0,5; 5/4. 3)-5,5; 1.
ІV кезең «Мерген» (слайд №17): Бұл кезеңде тиісті жолақтарды таңдау арқылы
әр топ берілген түбірлер бойынша теңдеулер құрып, шапшаңдықпен шыңның
басына шығу керек.
1-нші саты. Жауаптары.
Күлгін түсті жолақ:
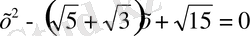
Жасыл түстіжолақ:
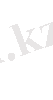
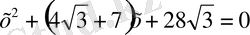
Қызыл түсті жолақ:
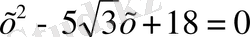
Сары түсті жолақ:
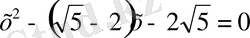
2-нші саты. Жауаптары.
Күлгін түсті жолақ:
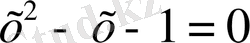
Жасыл түстіжолақ:
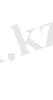
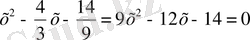
Қызыл түсті жолақ:
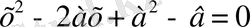
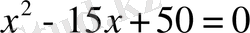3-нші саты. Екінші коэффициенті -15, ал түбірлерінің бірі екіншісінен екі
есе артық болатын квадрат теңдеу құрыңыз.
Жауабы. (слайд №21):
V кезең «Көкпар» (слайд №22): оқушылардың логикасы мен ой ұшқырлығын,
интеллектуалдығын бақылау сұрақтары:
1. ХV ғ. Самарқанд ғалымы, “Арифметика кілті” еңбегінің авторы? (Әл-
Каши).
2. Әріпті өрнекті енгізген ХVІ ғ фрацуздық көрнекті математик?
(Франсуа Виет).
3. “Хисаб ал-джебр вал-мукабала” еңбегінің авторы, ІХ ғ. Орта Азияның
белгілі математигі? (Әл–Хорезми).
4. Мектебіміздегі №15-і кабинет кімнің атымен аталған? (Жомарт Базенұлы).

3. Қорытындылау. ( слайд №23)
Кез келген квадрат теңдеуді шешуге болады. Ол үшін:
a) жалпы жағдайда ДИСКРМИНАНТТЫ табу формуласын біліуіміз қажет, оның үш
жағдайын. D>0. D=0. D<0;
b) Келтірілген квадрат теңдеу болғанда, оны Виет теремасы арқылы шешу;
c) a+b+c=0 және a+c=b дербес жағдайларды мұқият ескеру:
д) Рационал теңдеулерді шешкенде ең бірінші ММЖ-ны анықтау, БӨГДЕ түбірден
сақ болу.
4. Үйге тапсырма беру. № 182, 184. ( слайд №23)
5. Бағалау. ( слайд №24)

Шығамын десең биік шыңның басына,
Адал досың – Біліміңді ал қасыңа.
Зула, топ жар! Бәйгеге түс, бекем бол,
Тула, толқы, тебірен бірақ тасыма!

Назарларыңызға рахмет! Сабақ бітті.

-----------------------