Тікбұрышты үшбұрыштың катеттері мен гипотенузасы

Алматы қаласы

№104 жалпы білім беретін мектеп

Ануар Жанар Ануарқызы

математика пәні мұғалімі

10. 03. 2010 ж.

1. Сынып: 8 сынып 2. Мерзімі: 3. Пәні: геометрия

4. Тақырыбы: Пифагор теоремасы

5. Мақсаты:

Білімділік: Пифагор теоремасын және оған кері теореманы

тұжырымдап, дәлелдей алып, оларды есептер

шығаруда қолдана білу

Дамытушылық: Тікбұрышты үшбұрыштың қабырғалары мен бұрыштары

арасындағы байланыс туралы білімдерін олардың

қабырғалары арасындағы байланысқа ұласынтындығына

көз жеткізіп, білімдерін дамыту

Тәрбиелік: Ұқыптылыққа, тиянақтылыққа, мұқияттылыққа зер салу

6. Типі, әдісі, пәнаралық байланысы:

Жаңа білімді хабарлау, сұрақ-жауап тәжірибелік іздену,

математика, сызу, информатика

7. Көрнекілігі: Интерактивті тақта (флипчарт, слайдтар, бағалау

кестесі) Бағдарламалар: 1) Microft Office ( Excel, Power Point,

Word) ; 2) Activstudio; магнитті карталар, магнитті

кесінділер, үлестірмелер шаршы модельдері, жіп

8. Сабақтың барысы:

І. Ұйымдастыру: а) сыныптың сабаққа әзірлігін анықтау;

б) оқушылардың сабаққа әзірлігін анықтау;

в) мұғалімнің сабаққа әзірлігіне зер салу

ІІ. Сабақтың мақсатымен танысу

Рольдер:

Тақта және Экран - бейнелеуші

Мұғалім - бағыттаушы - бейне бойынша сұрақ қоюшы

Оқушы - ізденуші - бейнеге, оқулыққа назар аудара отырып, сұрақтарға жауап іздеп жауап беруші

ІІІ. Жаңа білімді қабылдауға даярлық:

Тірек ұғымдар:

Шаршы және оның ауданы;
Тікбұрышты үшбұрыш;
Тікбұрышты үшбұрыштың катеттері мен гипотенузасы;
Перпендикуляр, көлбеу және көлбеудің проекциясы;
Тікбұрышты үшбұрыштың сүйір бұрышының косинусы;
Пропорцияның негізгі қасиеті

IV. Жаңа сабақ:

Мұғалім: Тікбұрышты үшбұрыштың қабырғаларының арасындағы қатынасты өрнектейтін теореманы ашқан, грек оқымыстысы Пифагор (б. э. д. 580-500) . (Суреті көрсетіледі) .

Пифагор теоремасын және оған кері теореманы өз бетімізбен іздене отырып, тұжырымдап және оны ізденіс үстінде дәлелдейтін боламыз. Ол үшін «Не?, Қандай?, Қалай?» ойынын ойнаймыз.

І. «Не? Қандай? Қалай?» іздену, қимыл-жауап ойыны.

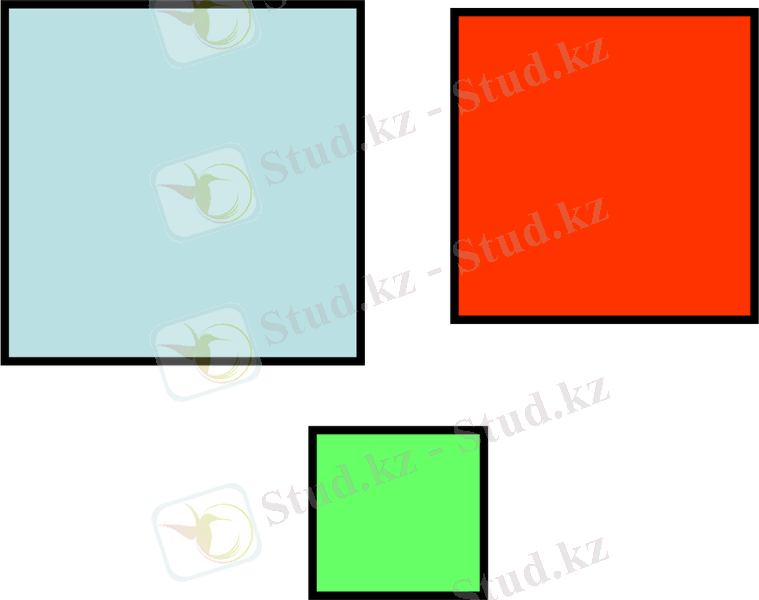Мұғалім: Сонымен, алдарыңыздағы фигураларға назар аударыңыздар.

(Оқушылардың парталарында, өздеріне жеке-жеке үш-үштен аудандары көрсетілген шаршылар болады. Бір үлгісі тақтада магнитті түрде көрсетіледі)

- Олар қандай фигуралар? (шаршылар)

- Қалай ойлайсыздар, ондағы өлшем нені білдіреді? (аудандарын)

- Шаршы аудандарының арасында қандай байланыс бар?(кішілерінің қосындысы үлкеніне тең)

- Әрбір екеуінінің тек бірғана ортақ төбесі болатындай етіп орналастыруға бола ма?(уақыт беріледі, оқушылар орналастырады, болады)

- Қандай біз білетін жазық фигура пайда болды?(үшбұрыш)

- Фигура - үшбұрыштың қай түрі?(тікбұрышты үшбұрыш)

- Ол фигураның қандай элементтері шаршылардың қандай элементтерімен қандай байланысы бар?( қабырғалары сәйкес)

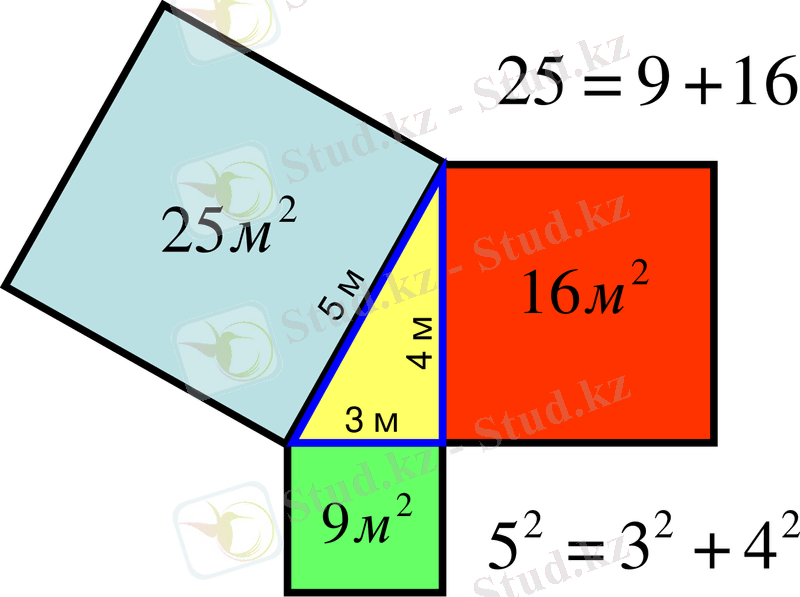- Одан қандай қорытындыға келуге болады?(катеттері квадраттарының қосындысы гипотенузаның квадратына тең)

Дұрыс, міне олай болса, осы қорытындыны келесі сауалдарға жауап қайтара отырып, келесі іздестіру жұмысын жүргізу барысында Пифагордың түйіндегенін дәлелдеп көрейік.

ІІ. Ол үшін оқулықтың 42 бетіндегі 21-теоремаға назар аударамыз.

Оқушы: (оқулықты қолына алып, дауыстап оқиды) .

Теорема: Тікбұрышты үшбұрыштың гипотенузасының квадраты катеттерінің квадраттарының қосындысына тең.

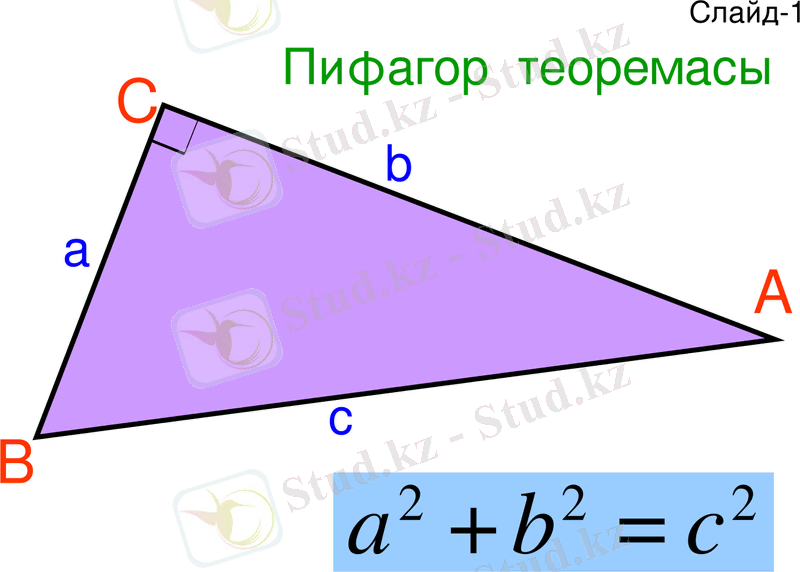
Экранда: Слайд-1.

(Тікбұрышты үшбұрыш, катеттері мен гипотенузасы және формула) .

Мұғалім: Осы тұжырымды дәлелдеуге назар аударалық. (Өзбетімен ізденеді, Слайд 2, Слайд 3, Слайд 4, Слайд 5, Слайд 6 бірінен соң бірі көрсетілгені әр слайдтағы, әрбір қимылды көріністен ой түйіндеп, ойларын ортаға салуға даярланады. ) (5 минут)

Мұғалім: Сөйлеймін деушілер бар ма?

Оқушы: (Оқушы формулаларды оқып, тұжырымды дәлелдейді)

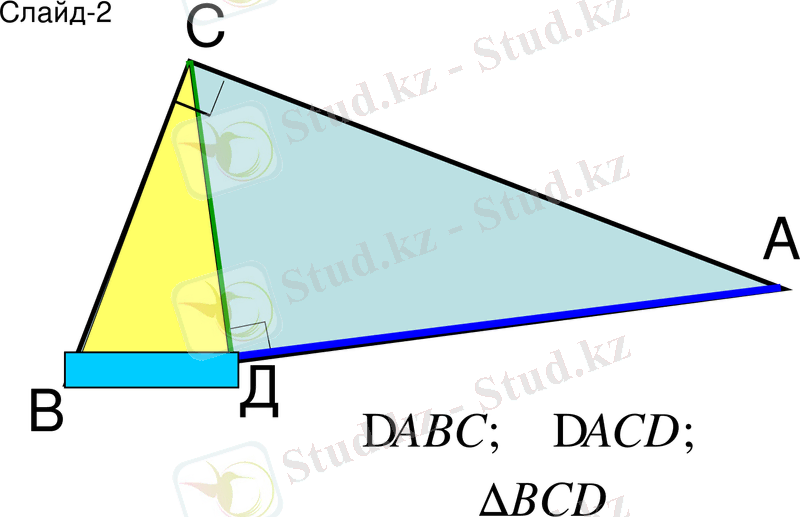
Экранда: Слайд-2.

Тікбұрышты үшбұрыштың тік бұрышынан гипотенузаға биіктік жүргізіледі;
Пайда болған тікбұрышты үшбұрыштарды атайды;

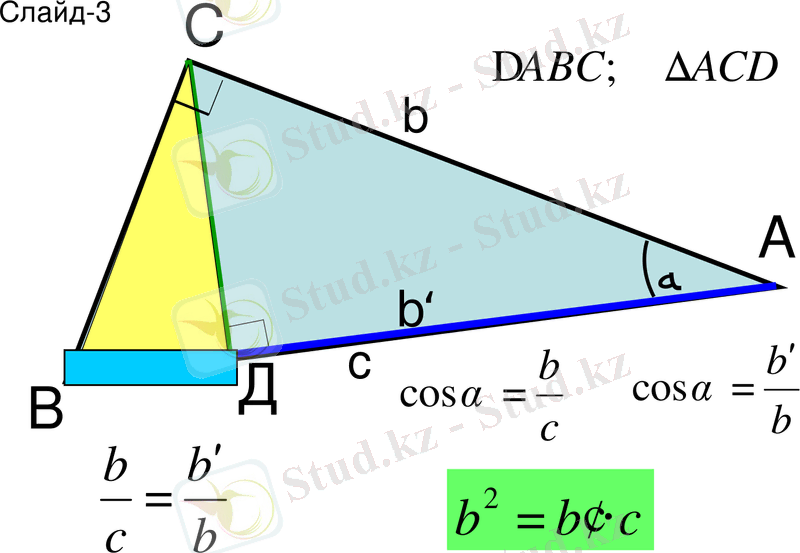
Слайд-3.

Сүйір бұрышы ортақ болатын тікбұрышты үшбұрыштарды атайды
Тік бұрыштардағы сүйір бұрыштардың косинустарын анықтайды;
Теңдіктердің оң жақ бөліктерін теңестіреді;
Пропорцияның негізгі қасиетіне сүйеніп, катеттің квадратын гипотенуза мен катеттің гипотенузадағы проекциясы арқылы өрнектейді.

Ұқсас жұмыстар

Тікбұрышты үшбұрыштың катеттерін табу

Сүйір бұрыштың тангенсі

Тікбұрышты үшбұрыш. Тікбұрышты үшбұрыштардың теңдігінің белгілері

Тікбұрышты үшбұрыштардың түрлері

Үшбұрыштың қабырғалары

Тікбұрышты үшбұрыш

Үшбұрыштың бүйір қабырғаларын тап

Пифагор теоремасына кері теорема

Үшбұрыш бұрыштары арқылы дәлелдеу

Іштей және сырттай сызылған шеңберлердің радиустарының үшбұрыш ауданымен байланысы

Пәндер