Теңсіздіктерді дәлелдеуге берілген есептер

Таңдау курсында
оқушыларды олимпиадаға даярлау
Алтынкул Онланова Есіркепқызы
№51 жалпы білім беретін орта мектептің мұғалімі
Математика саласында
талантты оқушылар
көп, көрсеткіштері де жақсы

А. Жұмаділдаев
Мектеп оқушыларын олимпиадаға даярлау өзекті мәселенің бірі болып
табылады. Есепті шешудің әр түрлі әдістері оқушының өз бетіменжұмыс
істеууінің негізі болып табылады. Оқыту процесі оқушыларды есеп шығаруға
үйрету десек, ол белгілі бір типтегі олипиадалық есептерді қарастыру
математикалық материалды меңгеруге тигізетін әдіс болып табылады. Сондықтан
оқыту барысында оқушыларды олимпиадалық есептер шығаруға үйретуге көп көңіл
бөлу қажет.
Тақырыптық жоспар
Таңдау курсында оқушыларды олимпиадаға даярлау
|Сабақ |Сабақтың тақырыбы |Сағат саны |
|№ | | |
|1-2 |Алгебралық теңдеулерді шешуге берілген есептер |2 |
|3-4 |Алгебралық теңдеулер жүйелерін шешуге берілген есептер |2 |
|5 |Көрсеткіштік және логарифмдік теңдеулерді шешуге |1 |
| |берілген есептер | |
|6 |Тригонометриялық теңдеулер мен олардың жүйелерін шешуге |1 |
| |берілген есептер | |
|7 |Функциялық теңдеулерді шешуге берілген есептер |1 |
|8 |Теңдеудің бүтін шешімдерін анықтау |1 |
|9 |Теңдеулер жүйесінің бүтін шешімдеріни анықтау |1 |
|10 |Дискриминанттық әдіске берілген есептер |1 |
|11 |Стандартты емес теңдеулерді шешуге берілген есептер |1 |
|12 |Стандартты емес теңсіздіктерді шешуге берілген есептер |1 |
|13 |Стандартты бөлінгіштігіне берілген есептер |1 |
|14 |Әртүрлі тақырыпқа берілген арифметикалық есептер |1 |
|15 |Жай және құрама сандарға берілген есептер |1 |
|16 |Әртүрлі тақырыпқа берілген параметрлі есептер |1 |
|17 |Сандарды салыстыруға берілген есептер |1 |
|18-19 |Теңсіздіктерді дәлелдеуге берілген есептер |2 |
|20 |Шартты теңсіздіктерді дәлелдеуге берілген есептер |1 |
|21 |Тригонометриялық теңсіздіктерді дәлелдеуге берілген |1 |
| |есептер | |
|22 |Геометриялық теңсіздіктерді дәлелдеуге берілген есептер |1 |
|23 |Көпмүшеліктерге берілген есептер |1 |
|24 |Арифметикалық және геометриялық прогрессияға берілген |1 |
| |есептер | |
|25 |Шартты теңбе-теңдіктерді дәлелдеуге берілген есептер |1 |
|26 |Өрнекті ықшамдау мен мәнін табуға және қосындыны |1 |
| |анықтауға берілген есептер | |
|27 |Ең үлкен және ең кіші мәнді табуға берілген есептер |1 |
|28 |Функцияның мәндерінің облысын табуға берілген есептер |1 |
|29 |Дирихле принципіне берілген есептер |1 |
|30 |Үшбұрыштар тақырыбына есептеуге берілген есептер |1 |
|31 |Үшбұрыштар тақырыбына дәлелдеуге берілген есептер |1 |
|32 |Төртбұрыштар тақырыбына берілген есптер |1 |
|33 |Көпжақтарға әртүрлі тақырыпқа берілген есептер |1 |
|34 |Геометриялық функцияның фигуралардың комбинациясына |1 |
| |берілген есептер | |
| |БАРЛЫҒЫ: |34 |
| |Құрастырған: Бейсеков Ж., Онланова А. | |

Төменде «Көрсеткіштік және логарифмдік теңдеулерді шешуге берілген
есептер» тақырыбы бойынша сабақ жоспарын ұсынып отырмын.
Сабақтың тақырыбы: Көрсеткіштік және логарифмдік теңдеулер.
Сабақтың мақсаты:
Білімділік мақсаты: а) оқушылардың математика пәніне деген қызығушылығын
арттыру.
ә) оқушының өзіндік ізденістерін қалыптастыру, ой-өрісін дамыту.
Дамытушылық мақсаты: Практикалық білім, дағды қалыптастыру, шапшаң есептеу
техникасын шыңдау.
Тәрбиелік мақсаты: Оқушыларды сабырлыққа, ұстамдылыққа шақыру, еңбектенуге
баулу, шығармашыл тұлға қалыптастыру.
Сабақтың түрі: Білімді жинақтау, жүйелеу.
Сабақтың әдісі: Түсіндірмелі жазбалар.
Сабақтың көрнекілігі: Интерктивті тақта.
Оқушының қызығушылығын арттыру: Халықаралық математикалық олимпиада – 1959
жылдан бері математика пәні бойынша жоғары сынып оқушылары арасында
өткізіліп келе жатқан дәстүрлі чемпионат.
2010 жылы 14 қаңтарда Алматы қаласында математика, физика,
информатика пәндерінен Шәутіков атындағы 6-шы халықаралық олипиада болды.
Мұнда 16 елдің оқушылары үш пәннен сайысқа түсті.
Қазақстан ЮНЕСКО-ның білім беруді дамыту индексі бойынша
көшбасшылардың төрттігіне енді.
Астана қаласында 2010 жылдың шілде айында математикадан 51-ші
халықаралық олимпиада болды. Осы олимпиададан Қазақстан, командасы -
әлемнің 98 елінің арасынан 5-ші орынға ие болды.
Сабақтың барысы:
1. Ұйымдастыру кезеңі:
Сынып тазалығына көңіл бөлу, оқушыларды түгелдеу. Оқушы назарын өзіме
аудару.
Сабақтың негізгі бөлімі:
Көрсеткіштік және логарифмдік теңдеулерді шешуге берілген есептер.
1–мысал. Теңдеуді шешіңдер:

Шешуі: Теңдеудің екі жағында бірдей -не бөлеміз.

Бұл теңдікті мына түрде жазуға болады:

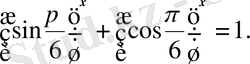
Бұл теңдеуді негізгі тригонометриялық теңбе-теңдікпен салыстыру, оның
түбірі х=2 саны деген қортындыға келеміз.
Теңдеудің сол жағындағы екі кемімелі функцияның қосындысы тұратындықтан,
теңдеудің басқа түбірі болмайды.
Жауабы: 2.
2–мысал. Теңдеуді шешіңдер:

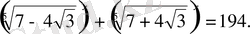
Шешуі: Теңдеудің екі жағын да 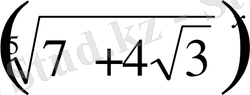-не көбейтіп, табатынымыз:

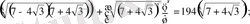
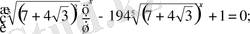
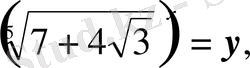мұндағы у>0 деп, белгілесек, онда берілген теңдеу мынадай түрге
келеді:

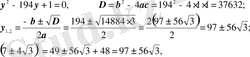
олай болса,

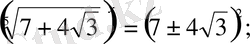
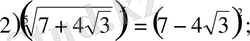
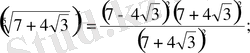
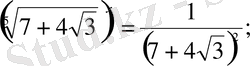
Жауабы: ±10.
3–мысал. Теңдеуді шешіңдер:

Шешуі: екенін ескеріп, табатынымыз:

Бұл теңдеу мына теңдеуге мәндес:
яғни

Теңдеудің анықталу облысын ескерсек, бұл теңдеудің тек бір ғана шешімі бар:

Жауабы: 1.
Оқушылардың өз бетімен есеп шығаруға тақтаға шығарамын.
Теңдеуді шешіңдер:
№5.

Жауабы: 3.
№9.
Жауабы:
Оқулықпен жұмыс
11 сынып. Алгебра және анализ бастамалары. Жартылыстану-математика бағыты.
С деңгей.
Теңдеуді шешіңдер:
№210. 2)
Жауабы: –2.
4)
Жауабы: ±2.
Сабақты қорытындылау
Оқушыларды есеп шығаруына қарай бағалаймын.
Үйге тапсырма: №1-15
Шымкент қаласы