Тригонометриялық теңдеулер және теңсіздіктер

Мұғалжар ауданы №7 орта мектеп

Тақырыбы: Күрделі тақырыптардағы есептерді шешу мысалдары

(жоғарғы сынып оқушыларына математикадан көмекші құрал)

Дайындаған: математика пәнінің мұғалімі Нұрбаева Ж. К.

2015 жыл

І. Оқушылардың функционалдық сауаттылығын дамытуға арналған жаттығулар

1. Суретте Қанаттың дүкеннен велосипед сатып алғандағы дүкенге бару және қайту қозғалысының графигі кескінделген. Қанаттың дүкенге барып-қайтқандағы орташа жылдамдығын табыңыз.

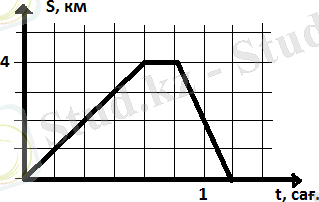
А) 4 км/сағ

В) 6 км/сағ

С) 12 км/сағ

Д) 8 км/сағ

Е) 9 км/сағ

Шығару жолы:

Қанаттың дүкенге баруға кеткен уақыты 40 мин. Ол дүкенде 10 мин сауда жасады, үйге қайту уақыты 20 мин. Барлық жүрген жолы 8 км. Жолда жүрген барлық уақыты 60 мин., яғни 1 сағ.

Орташа жылдамдық - Vорт. = $8\ км/1\$ сағ. =8 км/сағ.

Жауабы: Д) 8 км/сағ.

2. Бөлменің есігі жақтауларының ені бірдей болатындай етіп шынылған. Шынының ауданы 1, 8 м ² . Жақтаудың енін х деп алып, шынының ауданын табуға арналған теңдеуді көрсетіңіз.

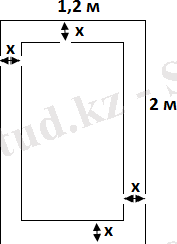
А) (1, 2-2х) (2-2х) =1, 8

В) 2(1, 2-2х) =1. 8

C) (1, 2-2х) х=1. 8

Д) (1, 2-х) (2-х) =1, 8

Е) 2(2-2х) =1. 8

Шығару жолы:

Шынының ені: 1, 2м-2х.

Шыны ұзындығы: 2м-2х

Шыны ауданы: (1, 2-2х) (2-2х) =1, 8м.

Жауабы: А)

3. Төмендегі диаграммада сыныптағы 31 оқушының үйірмелерге қатысуы берілген. Екі үйірмеге де неше оқушы қатысатынын табыңыз.

А) 7

В) 5

С) 8

Д) 6

Е) 4

Шығару жолы:

Сыныптағы барлық оқушы санынан үйірмеге қатыспайтын оқушылар санын алып тастаймыз.

31-5=26

Спорттық үйірмеге 19 оқушы, ал би үйірмесіне 12 оқушы қатысады, жалпы саны

19 +12=31.

Екі үйірмеге де қатысатын оқушылар саны

31-26=5.

Жауабы: С)

4. Құрылыс фирмасы 40 м ² құрылыс діңгектерін үш сатушыдан алуына болады. Бағалары мен жеткізу шарттары кестеде көрсетілген. Жеткізу шартымен есептегенде ең аз төлемақыны табыңыз.

А) 35500 тг.

В) 44000 тг.

С) 38500 тг.

Д) 37000 тг.

Е) 36000 тг.

Шығару жолы:

1- сатушы: 40*700=28000, 28000+1=38000. (мұнда жеңілдік жоқ)

2-сатушы: 40*900=36000 (мұнда жеткізу тегін)

3-сатушы: 40*750 =3, 3+8000=38000. (жеңілдікиі қолдана алмайды)

Үш бағаны салыстырып, екінші сатушының бағасының арзан екенін көреміз.

Жауабы: Е)

5. Суретте көрсетілген боялған төртбұрыштың ауданын табыңыз.

1cм

А) 26 см ² В) 27, 5 см ²

С) 28, 5 см ² Д) 29 см ²

Е) 31 см ²

Шығару жолы:

Төмендегідей белгілеулер енгізіп аламыз. Суреттегі фигуралардың төбелерін A, B, C, D, E, L, M, N. Толық аудан ABCD төртбұрышының ауданын есептейік:

S _ABCD =9*8=72 см ²

Боялған төртбұрыштың ауданын табу үшін боялмаған клеткалардың аудандарын тауып аламыз:

S _AKE = 3*7/2 = 10. 5 см ²

S _ECD = 6*8/2 = 24 см ²

S _LNC =2*7/2=7 см ²

S _KML =1*2/2=1см ²

S _KBNM = 2*1=2 см ²

Енді боялған жердің ауданын табу үшін жалпы ауданнан боялмаған ауданды алып тастаймыз:

S _KLCE = 72-10. 5-24-7-1-2 = 27, 5

Жауабы: В)

6. Төмендегі диаграммада үш оқушының математика пәнінен олимпиадаға қатысып, берілген он есептің нешеуін шығарғаны көрсетілген. Кем дегенде

неше есепті үш оқушы да шығарғанын табыңыз.

А) 5

В) 1

С) 3

Д) 4

Е) 2

Шығару жолы:

Әділханның шығармаған есеп саны: 10-9=1

Арманның шығармаған есеп саны: 10-6=4

Мақпалдың шығарған есептер санынан осы екі баланың шығармаған есептер санын алып тастаймыз:

7-1-4=2,

демек ең кем дегенде екі есепті үш оқушы да шығарған.

Жауабы: Е)

7. Ғаламтор провайдері үш тариф белгіледі:

Егер қолданушы айына 650 Мб қолданатын болса, осы қолданушы үшін ең арзан тарифті таңдап, бағасын есептеңіз.

А) 825 тг.

Б) 750 тг.

С) 650 тг.

Д) 850 тг.

Е) 700 тг.

Шығару жолы:

1. «0»-дік тарифте 650*1, 5 =975 тг.

2. «400»-дік тарифте 400+(650-500) *2 =700 тг.

3. «600»-дік тарифте 600+(650-550) *2 = 800 тг.

Осы үш бағаны салыстырып, ең арзаны 700 тг. екенін анықтаймыз.

Жауабы: Е)

8. Екі жолаушы Арқалықтан Астанаға барғанда пойызбен немесе автокөлікпен барғанда қаражат үнемдеу жолын ойластырды. Пойыз билетінің құны бір адамға 2655 тг. Автокөлік 100 км жолға 10 л жанармай жұмсайды, ал жанармай бағасы бір литрге 110 тг. Автокөлікпен жүрген жолдың ұзындығы 400 км. Ең аз дегенде екі адамға қанша теңге төленеді?

А) 4650 тг.

В) 5455 тг.

С) 5280 тг.

Д) 5310 тг.

Е) 4400 тг.

Шығару жолы:

1. Пойызбен : 1 адамға 2655 тг.

2 адамға: 2*2655 =5310 тг.

2. Автокөлікпен:

100 км-ге 10 л жұмсаса,

400 км-ге 40 л жанармай жұмсалды: 4*10л =40л,

1 л жанармай 110 тг болса,

40 л жанармай:

110*40 =4400 тг.

Салыстырсақ: пойызбен екі жолаушы 5310 тг., автокөлікпен екі жолаушы 4400 тг. жұмсайды

Жауабы: Е)

9. Үш фирманың біреуіне көрмені шынылау үшін 100 бірдей шыныға тапсырыс беруге болады. Әр шынының ауданы 0, 5 м ² . Кестеде шыны мен оны кесу бағалары көрсетілген. Ең тиімді тапсырысқа қанша теңге төленетінін анықтаңыз.

А) 4500 тг.

В) 4100 тг.

С) 4400 тг.

Д) 3750 тг.

Е) 4250 тг.

Шығару жолы:

100 шынының ауданы: 0, 5*100 =50 м ²

І фирма: 70*50+ 100*10=3500+1000=4500тг.

ІІ фирма: 80*50=4000 тг. Қосымша шарттарды пайдаланып, шыны бағасынан 10 %-ды алып тастаймыз:

4000-400=3600 тг.

Кесу бағасы: 100*8=800 тг.

Жалпы бағасы: 3600+800 = 4400 тг.

ІІІ фирма: 75*50=3750

3750+500=4250 тг.

Үш фирманың бағасын салыстырып, үшінші фирманың бағасы арзан екенін көруге болады.

Жауабы: Е)

10. Қамырдан 20 бірдей қалаш немесе 25 бірдей тоқаш жасауға болады. Егер бір қалашқа тоқашқа қарағанда 10 г қамыр артық кететін болса, барлық қамырдың салмағы қандай болғаны?

А) 750 г

В) 1 кг

С) 2 кг

Д) 1, 5 кг

Е) 500г

Шығару жолы:

Бір тоқашқа кететін қамыр х гр.

Бір қалашқа кететін қамыр х+10 гр.

(х+10) $\ \bullet$ 20 = 25х

20х+200 = 25х

5х = 200

X = 40

Барлық қамыр 25х = 25 $\ \bullet \$ 4 = 1000гр = 1кг

Жауабы: В

ІІ. Логикалық есептер

1. Раушан, Орал және Маржан жеңіл атлетикадан Қазақстан турниріне қатысты. Раушан жүгірумен, дискі лақтырумен айналыспайды. Орал - жүгірумен айналыспайды, ал Маржан ұзындыққа секіру және дискі лақтырумен айналыспайды. Турнирге кім спорттың қай түрімен қатысты?

Шығару жолы:

жүгіру -

Раушан дискі лақтыру -

ұзындыққа секіру +

ұзындыққа секіру -

Маржан дискі лақтыру -

жүгіру +

жүгіру -

Орал дискі лақтыру +

ұзындыққа секіру -

Жауабы: Раушан -ұзындыққа секіру, Орал - дискі лақтыру, Маржан - жүгіру

2. Зообақ қызметкері кенгуру әр қыс сайын 5 кг-ға толықтап, әр жаз сайын 4 кг-ға жүдейтін, ал көктем мен күзде салмағы өзгермейтінін байқаған. 2008 жылы көктемінде кенгуру салмағы 100 кг болса, 2004 жылы күзінде оның салмағы қандай болған?

Шығару жолы:

2004ж - күз х

2004ж - қыс, желтоқсан х+5

2005ж - қыс, қаңтар, ақпан

2005ж - жаз x+5-4=x+1

2005ж - қыс, желтоқсан

2006 ж - қыс, қаңтар х+1+5=х+6

2006ж - жаз х+6 - 4=х+2

2006 ж -қыс, желтлқсан

2007ж-қыс, қаңтар х+2+5=х+7

2007ж - жаз х+7-4=х+3

2007ж - қыс, желтоқсан

2008ж - қыс, қаңтар х+3+5=х+8

100кг

2008 ж - көктем 100кг

Х+8=100

х=92кг

Жауабы: 92 кг

3. Алдар көсе бір байдың үйіне жұмысқа жалданады. Бір жылдық жұмыс істегені үшін 1 жылқы және 100 000 теңге алу керек болатын, бірақ ол 7 айдан кейін жұмыс істегісі келмей, жұмыстан кетеді. Өзімен 1 жылқы және 2 теңге алып кетеді. 1 жылқының құны қанша?

Шығару жолы:

1 жыл=12 айда 1 жылқы 100 000 тг

7 айда 1 жылқы 20 000 тг

Сонда:

5 айда = 80 000 тг

Демек:

1 айда = 16 000 тг

Бұдан: 1 жыл = 12 айда 16 000 тг * 12 = 192 000тг

Сонда 1 жылқы құны 192 000 тг - 100 000тг = 92 000 тг

Жауабы: 92 000 тг

4. Ондық цифрлары бірліктер цифрларынан улкен болатын қанша екі таңбалы сан бар?

Шығару жолы:

10, 1 сан

20, 21, 2 сан

30, 31, 32 3 сан

. . .

. . .

90, 91, 92, 93, 94, 95, 96, 97, 98 9 сан

Жалпы: 1+2+3+4+5+6+7+8+9=45

Жауабы: 45 сан

5 . Ұлы, қызы, шешесіүшеуі бірігіп бірнеше теңге жұмсаған. Ұлы мен шешесі 320 тг, ұлы мен қызы 250 тг, ал қызы мен шешесі 200 тг жұмсаған. Барлығы қанша теңге жұмсаған.

Шығару жолы:

ұ+қ+ш=х

ұ + ш = 320

ұ+қ = 250

ш+қ = 200

Бұдан:

ш қ =70

+ ш+қ = 200

2ш = 270 қ = 135 - 70

ш = 135 қ =65

ұ = 320-135

ұ = 185 Демек: ш+қ+ұ =135+185+65=385

Жауабы: 385 тг

6. Электронды сағат уақытты сағат және минутпен көрсетеді. (00:00 - 23:59 аралығы) . Бір тәулікте бұл сағаттың көрсеткішінен мына 2, 0, 1, 8 цифрларын неше рет көруге болады? (кез - келген ретте)

Шығару жолы:

01:28, 02:18, 08:12, 08:21, 10:28, 12:08, 18:02, 18:20, 20:18, 21:08

Жауабы: 10 рет

7. Автотұрақта бес машина бірінен соң бірі тұр. «Волга» «Мерседестің» алдында, «Ауди» «Тайотадан» кейін. «Мерседес» «Лексустың» алдында, «Лексус» «Тайотаның» алдында тұр. Тұрақта машиналар қандай ретпен тұр?

Шығару жолы:

«Волга» «Мерседестің» алдында: ВМ

«Ауди» «Тайотадан» кейін: ТА ВМЛТА

«Мерседес» «Лексустың» алдында: МЛ

«Лексус» «Тайотаның» алдында: ЛТ

Жауабы: Волга, Мерседес, Лексус, Тайота, Ауди.

8. 3 ¹⁰⁰⁰ саны қандай цифрмен аяқталады?

Шығару жолы:

1000 / 4=250 3 ¹ = 3 3 ⁵ =243 . . .

3 ² = 9 3 ⁶ =729 . . .

3 ³ = 27 3 ⁷ = 2187 . . .

3 ⁴ = 81 3 ⁸ = 6561 . . .

Жауабы: Демек: 3 ¹⁰⁰⁰ тең саны 1 цифрымен аяқталады.

9. А, В, С - әртүрлі оң цифрлар санымен қатар АВС * АВС = 207936.

Бұл цифрлардың қосындысын табыңдар: А+В+С=?

Шығару жолы:

АВС*АВС =(АВС) ² = 207936

АВС = 456

А+В+С = 4+5+6 = 15

Жауабы: 15

10. Бір газеттің жалпы бетінің саны 48 және оның ішіндегілердің барлығы тек екібеттік қағаздар. Осы газеттен әрбір екі беттігін алып ашып қарағанда, беттік нөмірлерініңқосындысы қандай да бір тақ санды береді. Ол қай сан?

Шығару жолы:

2 - ші бет пен 47 - ші бет

2+47=49

Жауабы: 49

ІІІ. Мәтін есептер

1. Катер өзен ағысымен 15 км және 4 км тынық суда жүзді. Барлық жолға 1 сағ уақыт кетті. Өзен ағысының жылдамдығы 4 км/сағ болса, онда катердің өзен ағысымен жүзгендегі жылдамдығын табыңыз.

Шығару жолы:

$s = vt\$ жолдың формуласынан

t $= \frac{s}{v}; \$

сонда $\frac{15}{v + 4} + \frac{4}{v} = 1$

$\frac{\ 15v + 4v + 16}{v(v + 4) } = 1$

$19v + 16 = v^{2} + 4v$

$v^{2} - 15v$ -16=0

D=225+64=289

$v_{1} = \frac{15 - 17}{2} = - 1$ ; $v_{2} = \frac{15 + 17}{2} = 16$

Сонда катер өзен ағысымен жүзгенде 16км/сағ. + 4км/сағ. =20км/сағ.

Жауабы: 20 км/сағ.

2. Құны 225 мың теңгелік екі бағалы тері халықаралық аукционда 40 % пайдамен сатылды. Егер бірінші теріден 25%, екіншісінен 50% пайда түскен болса, әр терінің жеке бағасы қанша?

Шығару жолы:

$\left\{ \begin{array}{r} x + y = 225 \\ 1, 25x + 1, 5y = 225 + 0, 4 \bullet 225 = 315 \end{array} \right. \$

Бірінші теңдеуден $\$ y=225-x, екінші теңдеуге қойып:

1, 25x+1, 5(225-x) =315

1, 25x+337, 5-1, 5x=315

-0, 25x=-22, 5

x=90

y=225-90=135

Жауабы: 135 мың және 90 мың теңге.

3. Жинақ кассасынан ақша сақтаушы кісі әуелде өз ақшасының $\frac{1}{4}\$ бөлігін алып, екінші рет қалған ақшасының $\frac{4}{9}$ бөлігін және 640 тг алды. Ақшасын екі рет алғаннан кейін жинақ кітапшасында барлық салған ақшасының $\frac{3}{20}$ бөлігі қалды. Басында салған ақшасының мөлшері қандай еді?

Шығару жолы:

Әуелде салған ақшасын х деп аламыз. Сонда бірінші рет $\frac{1}{4}x$ ақша алғанда $x - \frac{1}{4}x = \frac{3}{4}x$ ақшасы қалды. Екінші рет қалған $\frac{3}{4}x$ ақшаның $\frac{4}{9}$ бөлігін және 640 тг алды.

Сонда: $\frac{3}{4}x \bullet \frac{4}{9} = \frac{1}{3}x$ ,

демек $\frac{3}{4}x - \frac{1}{3}x - 640 = \frac{3}{20}x$ ,

$\frac{5}{12}x - \frac{3}{20}x = 640$

$$\frac{16}{60}x = 640$$

$$\frac{4x}{15} = 640$$

x=2400

Жауабы: 2400 тг.

4. Екі кран бірлесе жұмыс жасай отырып, баржадағы жүкті 6 сағатта түсіріп болды. Егер олардың біреуі екіншісіне қарағанда жүкті 5 сағатқа ерте түсіретін болса, онда олардың әрқайсысы жүкті неше сағатта түсіріп болар еді?

Шығару жолы: $\frac{1}{x} + \frac{1}{x - 5} = \frac{1}{6}$ ;

$\frac{2x - 5}{x(x - 5) } = \frac{1}{6}$ ;

x ² -17x+30=0

D=289-120=169

$x_{1} = \frac{17 - 13}{2} = 2$ ; $x_{2} = \frac{17 + 13}{2} = 15$

Жауабы: x=15 сағ.

х - 5=15 - 5=10 сағ.

5. Ара қашықтығы 900 км екі қаладан бір-біріне қарама-қарсы екі пойыз шығып, олар жол ортада кездескен. Бірінші пойыз екіншісінен 1 сағат кеш шығып, екінші пойыздың жылдамдығынан 5км/сағ артық жылдамдықпен жүрген. Әр пойыздың жылдамдығын табыңыз.

Шығару жолы:

Пойыздар жол ортада кездескендіктен, олардың әрқайсысы 450 км жол жүр-ген. Бірінші пойыздың жылдамдығы v+5, екінші пойыздың жылдамдығы v.

$\frac{450}{v + 5} = \frac{450}{v} - 1$

$\frac{450v - 450v - 2250}{v(v + 5) } = - 1$

v ² +5v-2250=0

D=25+9000=9025=95 ²

$v_{1} = \frac{- 5 - 95}{2} = - 50$ ; $v_{2} = \frac{90}{2} = 45$

Жауабы: v =45км/сағ.

v +5 км/сағ = 50 км/сағ.

6. Фотоаппараттың бағасын екі рет бірдей процентке арзандатқанда оның бағасы 300 тг-ден 192 тг-ге түсті. Фотоаппараттың бағасы екі ретінде де неше пайызға арзандатылған?

Шығару жолы:

300 →100%

a → х%

$a = \frac{300x}{100} = 3x$

Бірінші арзандатылғаннан кейінгі бағасы 300 - 3х болды.

300 - 3х→ 100%

b→ x%

$b = \frac{(300 - 3x) x}{100} = 3x - 0. 03x$ ²

Екінші рет арзандатылғаннан кейінгі бағасы:

300 - 3х - 3х+0, 03х ² =192

0, 03х ² - 6х + 108 =0

D=36 - 12, 96=23, 04=4, 8 ²

$x_{1} = \frac{6 - 4, 8}{2 \bullet 0, 03} = \frac{1, 2}{0, 06} = 20$

Жауабы: Фотоаппараттың бағасы екі рет 20%-ға арзандаған.

7. Тауардың бағасы алдымен 20%-ға, одан кейін жаңа бағасын тағы да 25%-ға кемітті. Тауардың бастапқы бағасын неше процентке кеміткен?

Шығару жолы:

Тауардың бағасын х деп аламыз. Сонда: х →100%

0, 2х → 20%

Бірінші рет арзандатқаннан кейінгі бағасы х - 0, 2х =0, 8х. Енді 0, 8х→100%

0, 2х→25%

Екінші рет арзандатқаннан кейінгі бағасы 0, 8х - 0, 2х=0, 6х.

Алғашқы бағасы х, соңғы бағасы 0, 6х. Демек, х - 0, 6х=0, 4х, яғни 40%-ға арзандаған.

Жауабы: 40%

8. Теңіз суының құрамында 5% тұз бар (массасы бойынша) . 80 кг теңіз суына, ондағы тұздың мөлшері 4 % болуы үшін қанша тұщы су құю керек?

Шығару жолы:

80 кг→100%

х →5%

$x = \frac{80 \bullet 5}{100} = 4$ , демек: х =4 кг тұз бар.

Сонда 4 кг →4%

100 кг→100%

100 кг - 80 кг = 20 кг.

Жауабы: 20 кг тұщы су керек.

9. Картоп егілген жердің бір бөлігінің ауданы екіншісіне қарағанда 2 га артық. Бірінші бөліктен 748 тонна, екіншісінен 720 тонна картоп жиналды. Егер екінші бөліктің 1 гектарынан жиналған картоп бірінші бөліктің 1 гектарынан жиналған картоптан 4 тоннаға көп болса, онда әр бөліктің 1 гектарынан қанша картоп жиналды?

Шығару жолы:

Бірінші бөліктің өнімділігі х,

ауданы y+2

Екінші бөліктің өнімділігі х+4

Ауданы y деп алып, төмендегі жүйеге ие боламыз:

$\left\{ \begin{array}{r} x(y + 2) = 748 \\ y(x + 4) = 720 \end{array} \right. \$

Екінші теңдеуден: $y = \frac{720}{x + 4}$ . Осыны бірінші теңдеуге қойып:

$x \bullet \left( \frac{720}{x + 4} + 2 \right) = 748$

$\frac{720x}{x + 4} + 2x = 748\$

2x ² +728x - 748x - 2992 =0

2x ² - 20x - 2992 =0

x ² - 10x - 1496 =0

D=100+5984=6084=78 ²

$x = \frac{10 + 78}{2} = 44$

Жауабы: Бірінші бөліктің өнімділігі х =44 тонна

Екіншісі бөліктің өнімділігі х+4=48 тонна

10. Екі мотоциклші бір мезгілде бір-біріне қарамаса-қарсы А мен В пунктерінен шыққан. Олардың ара қашықтығы 600 км. Бірінші мотоциклші 250 км жүргенде екіншісі 200 км жүреді. Бірінші мотоциклші В-ға екіншінің А-ға жеткен уақытынан 3 сағат бұрын жетеді. Олар бірқалыпты қозғалады деп есептеп, мотоциклшілердің жылдамдықтарын табыңдар.

Шығару жолы:

v ₁ - бірінші мотоциклшінің жылдамдығы

v ₂ - екінші мотоциклшінің жылдамдығы

$\frac{250}{v_{1}} = \frac{200}{v_{2}}$ ;

200v ₁ =250v ₂

v ₁ =1, 25v ₂

$\frac{600}{v_{1}} = \frac{600}{v_{2}} - 3$

$\frac{600}{1, 25v_{2}} = \frac{600}{v_{2}} - 3$

480=600 - 3v

v ₂ =40

демек, v ₁ =1, 25v ₂ =1, 25 $\ \bullet \$ 40=50.

Жауабы: 40 км/сағ., 50 км/сағ.

ІV. Логорифмдік теңдеулер, теңсіздіктер және олардың жүйелері

1. Теңсіздіктер жүйесін шешіңіз:

$\left\{ \begin{array}{r} (5x + 2) \log_{0, 2}2 + 18\log_{0, 2}2 < 0 \\ \frac{4^{x} + 3℃ \bullet 2^{x} - 4}{x^{2} + x + 3} < 0 \end{array} \right. \$ $\left\{ \begin{array}{r} \log_{0, 2}2^{5x + 4} + \log_{0, 2}2^{18} < 0 \\ \frac{2^{2x} + 3 \bullet 2^{x} - 4}{x^{2} + x + 3} < 0 \end{array} \right. \$

Шығару жолы:

Жүйедегі бірінші теңсіздікті шығарамыз:

$$\log_{0, 2}(2^{5x + 2} \bullet 2^{18}) < 0$$

$$2^{5x + 2 + 18} > {0, 2}^{0}$$

$$2^{5x + 20} > 1$$

$$2^{5x + 20} > 2^{0}$$

$$5x + 20 > 0$$

$$5x > - 20$$

$$x > - 4$$

- 4

Екінші теңсіздікті шешу үшін жаңа айнымалыны енгіземіз:

$\left( 2^{2x} + 3 \bullet 2^{x} - 4 \right) \left( x^{2} + x + 3 \right) < 0$ теңсіздігінен

$2^{2x} + 3 \bullet 2^{x} - 4 = 0$ $x^{2} + x + 3 = 0$

$y^{2} + 3y - 4 = 0$ D= 1 - 12 = - 11

D=9 + 16 = 25

$y_{1} = \frac{- 3 - 5}{2} = - 4$

$y_{2} = \frac{- 3 + 5}{2} = 1$

$$2^{x} = y$$

$2^{x} \neq - 4$

$$2^{x} = 1$$

x = 0

Жауабы: (- 4; 0)

2. Теңдеуді шешіңіз:

$\log_{3}\left( 3^{x^{2} - 13x + 28} + \frac{2}{9} \right) = \log_{5}0, 2$

Шығару жолы:

Теңдеудің оң жағындағы

$\log_{5}0, 2 = \log_{5}\frac{2}{10} = \log_{5}\frac{1}{5} = - 1$ сонда,

$\log_{3}\left( 3^{x^{2} - 13x + 28} + \frac{2}{9} \right) = - 1$ бұдан

$3^{x^{2} - 13x + 28} + \frac{2}{9} = \frac{1}{3}$

$3^{x^{2} - 13x + 28} = \frac{1}{3} - \frac{2}{9} = \frac{1}{9} = 3^{- 2}$

$x^{2} - 13x + 28 = - 2$

$$x^{2} - 13x + 30 = 0$$

$$D = 169 - 120 = 49$$

$x_{1} = \frac{13 - 7}{1} = 3$

$x_{2} = \frac{13 + 7}{2} = 10$

Жауабы: x ₁ =3; x ₂ =10

3. Теңсіздікті шешіңіз:

$1 - 5\log_{x}2 + 6\log_{x}^{2}2 < 0$

Шығару жолы:

Жаңа айнымалыны енгізу арқылы y=log _x 2 квадрат теңдеу аламыз:

$6y^{2} - 5y + 1 < 0$

$D = 25 - 24 = 1$

$y_{1} = \frac{5 - 1}{12} = \frac{4}{12} = \frac{1}{3}$

$y_{2} = \frac{6}{12} = \frac{1}{2}$

Бұдан $\log_{x}2 = \frac{1}{3}$ және $\log_{x}2 = \frac{1}{2}$

$x^{\frac{1}{3}} = 2$ $x^{\frac{1}{2}} = 2$

x = 2 ³ x = 2 ²

x = 8 x = 4

Жауабы: (4; 8)

4. Теңсіздікті шешіңіз:

$$5 \bullet {0, 2}^{\lg_{x}} > {0, 2}^{{2lg}_{2}}$$

Шығару жолы:

$5 \bullet \left( \frac{1}{5} \right) ^{lgx} > {0, 2}^{lg4}$

$5 \bullet \left( \frac{1}{5} \right) ^{lgx} > \left( \frac{1}{5} \right) ^{lg4}$

$$\left( \frac{1}{5} \right) ^{- 1} \bullet \left( \frac{1}{5} \right) ^{lgx} > \left( \frac{1}{5} \right) ^{lg4}$$

$- 1 + lgx < lg4$

$lgx < lg4 + 1$

$$lgx < lg4 + lg10$$

$$lgx < lg(4 \bullet 10)$$

$$lgx < lg40$$

x $< 40$

Жауабы: Логорифмдік функцияның анықталу аймағын есепке алып, х > 0 болғандықтан, шешімі (0; 40)

5. Теңсіздікті шешіңіз:

Тригонометриялық теңдеулер жүйелерін шешу әдістері

Сағат саны

Тригонометриялық теңдеулер мен теңсіздіктер

Теңдеуге есептер шешу

Кері тригонометриялық функциялар

Сызықтық емес теңдеулер жүйесін шешу тәсілдері

«біртұтас педагогикалық процесті технологияландыру» атты жоба бойынша жасалған күнделікті сабақ жоспарының жобасы

Функциялар және графиктер

Бүтін рационал теңдеу

Ұбтға дайындық математика

• Іс жүргізу
• Автоматтандыру, Техника
• Алғашқы әскери дайындық
• Астрономия
• Ауыл шаруашылығы
• Банк ісі
• Бизнесті бағалау
• Биология
• Бухгалтерлік іс
• Валеология
• Ветеринария
• География
• Геология, Геофизика, Геодезия
• Дін
• Ет, сүт, шарап өнімдері
• Жалпы тарих
• Жер кадастрі, Жылжымайтын мүлік
• Журналистика
• Информатика
• Кеден ісі
• Маркетинг
• Математика, Геометрия
• Медицина
• Мемлекеттік басқару
• Менеджмент
• Мұнай, Газ
• Мұрағат ісі
• Мәдениеттану
• ОБЖ (Основы безопасности жизнедеятельности)
• Педагогика
• Полиграфия
• Психология
• Салық
• Саясаттану
• Сақтандыру
• Сертификаттау, стандарттау
• Социология, Демография
• Спорт
• Статистика
• Тілтану, Филология
• Тарихи тұлғалар
• Тау-кен ісі
• Транспорт
• Туризм
• Физика
• Философия
• Халықаралық қатынастар
• Химия
• Экология, Қоршаған ортаны қорғау
• Экономика
• Экономикалық география
• Электротехника
• Қазақстан тарихы
• Қаржы
• Құрылыс
• Құқық, Криминалистика
• Әдебиет
• Өнер, музыка
• Өнеркәсіп, Өндіріс