Дәрежелік функция: анықтамасы, қасиеттері және графигін салу әдістері


Ақпараттық: Студенттерді дәрежелік функция ұғымымен таныстырып, дәрежелік функцияның анықтамасы мен қасиеттерін (өсу, кему, және жұп-тақтығы) беру, графиктерін салуды меңгерту.
Коммуникативтік: Нақты анықтамалар мен қасиеттерді пайдалана отырып дәрежелік функциялардың графигін салуды үйрету, жүйелі түрде жұмыс істеуді қалыптастыру, өз ойын дәл, студенттерді белсенділікке, жинақтылыққа, математикалық тілде сөйлей білуге тәрбиелеу.
Проблеманы шешу: Студенттердің күтілетін нәтижеге бағытталған ақыл-ой әрекетін проблема қою және шешу арқылы ұйымдастыруда өз қызметінің нәтижесін бағалауға бағыттау, есептер шығаруда дәрежелік функцияның қасиеттерін қолдануды үйрету.
үйге берілген тапсырмалар:
log 3 x=log 3 1. 5+log 3 8. 2) 2log 25 (4х-3) =1.
log
3-x
5-
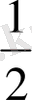 =0. 4)
=0. 4)
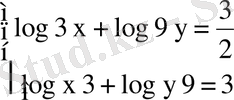
5)
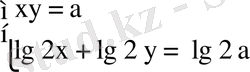 6)
6)
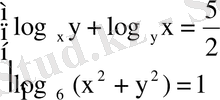
Сұрақтар.
1) Натурал логорифм дегеніміз неқ
2) Логарифмнің негізгі қасиеттерін көрсетқ
Жауаптары:
Натурал логорифм дегеніміз
- негізі е болатын логарифм, яғни

 =
=
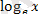
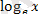 екені белгілі. Негізгі логорифмдік тепе - теңдік бойынша
екені белгілі. Негізгі логорифмдік тепе - теңдік бойынша
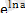
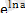 =
=
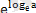
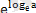 = а. Сондықтан кез келген у = а
х
көрсеткіштік функциясын былай жаз аламыз: а
х
=
= а. Сондықтан кез келген у = а
х
көрсеткіштік функциясын былай жаз аламыз: а
х
=
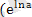
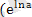 )
х
=
)
х
=
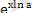
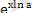 , яғни а
х
=
, яғни а
х
=
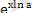
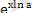
Логарифмнің негізгі қасиеттері:
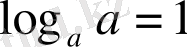 ,
,
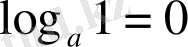
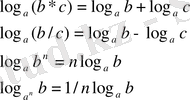
Жоспары:
1. Дәрежелік функция
2. Дәрежелік функцияның қасиеттері мен графигі
Жауаптары:
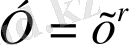 -дәрежелік функция, х-тәуелсіз айнымалы,
-дәрежелік функция, х-тәуелсіз айнымалы,
r-кез келген рационал сан.
Көрсеткішіне байланысты дәрежелік функцияның түрлерін қарастырайық.
r -натурал сан болса,
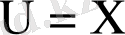 n
натурал көрсеткішті дәрежелік функция.
n
натурал көрсеткішті дәрежелік функция.
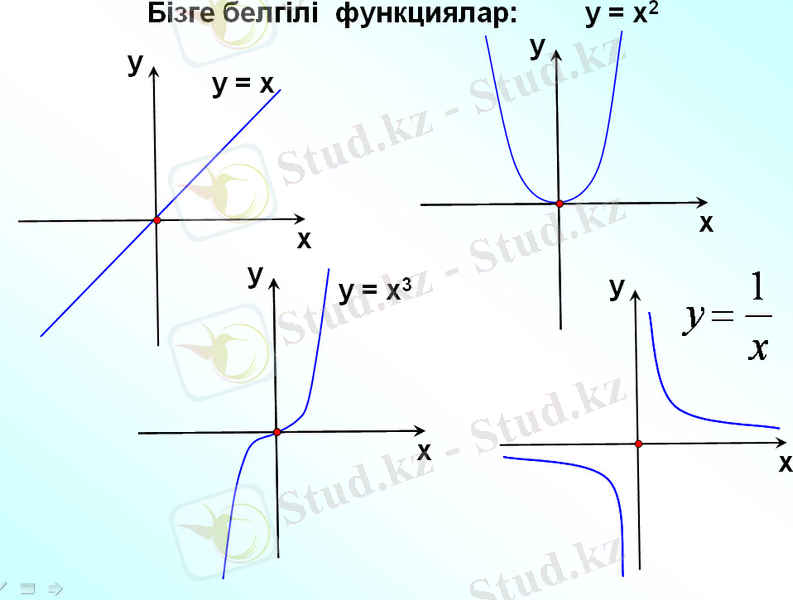
n=1, у =х графигі түзу сызық.
n=2, у=х 2 графигі парабола.
n=3, у=х 3 графигі кубтық парабола.
N=-1, y=1/x гипербола
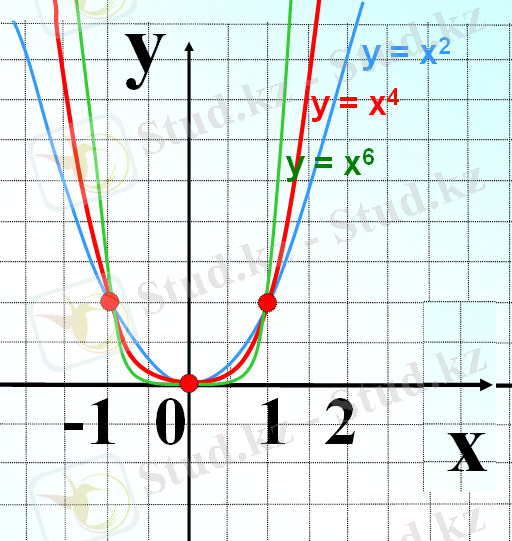
n=2k және n=2k+1 болғанда y=x n функциясының қасиеттері
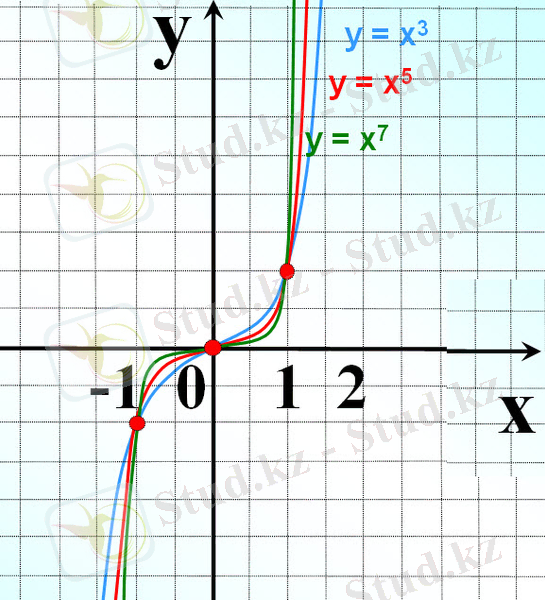
2. r - бүтін теріс сан (r=-n)
y=x
-n
=
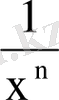 - бүтін теріс көрсеткішті дәрежелік функция.
- бүтін теріс көрсеткішті дәрежелік функция.
n - жұп сан ј) n - тақ сан
n = 2, y=
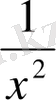 n = 1, y =
n = 1, y =

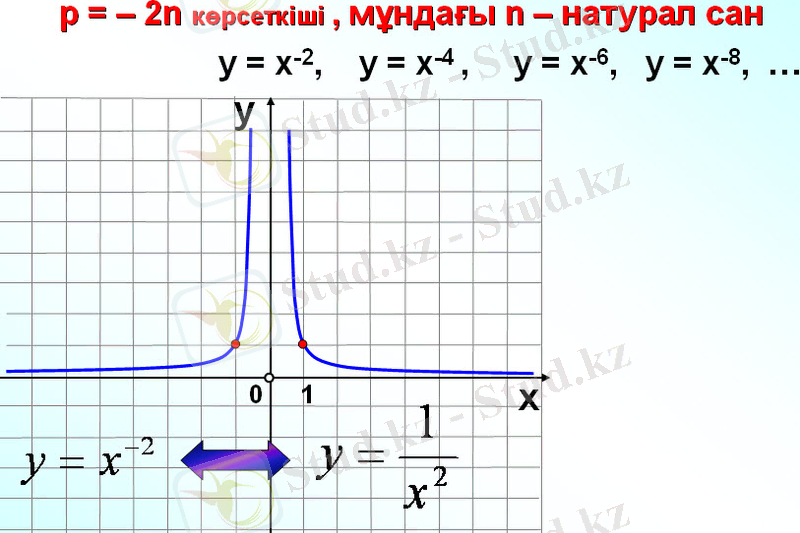
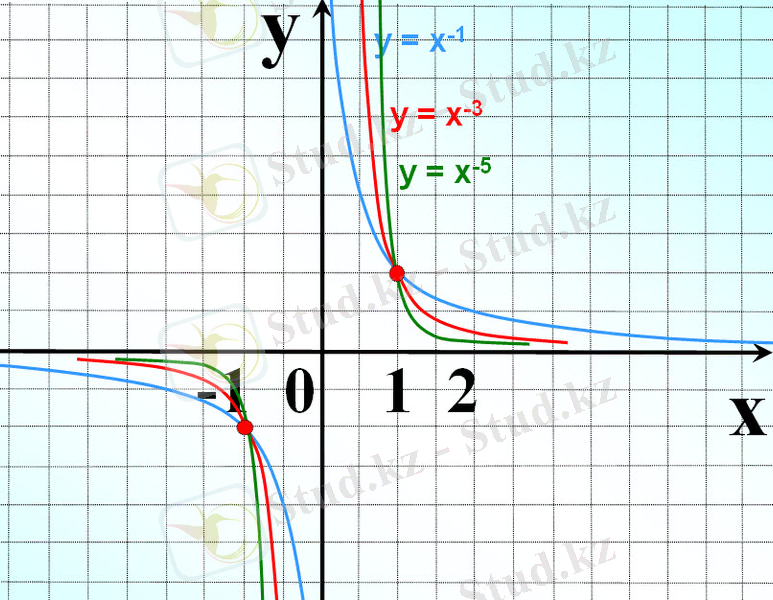
n=2k және n=2k+1 болғанда y=
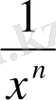 функциясының қасиеттері
функциясының қасиеттері
3. r =
 , n>1 y= x
, n>1 y= x
 =
=
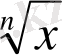 дәрежелік функция
дәрежелік функция
Мысалы. n=2, y=x
 n=3, y=x
n=3, y=x

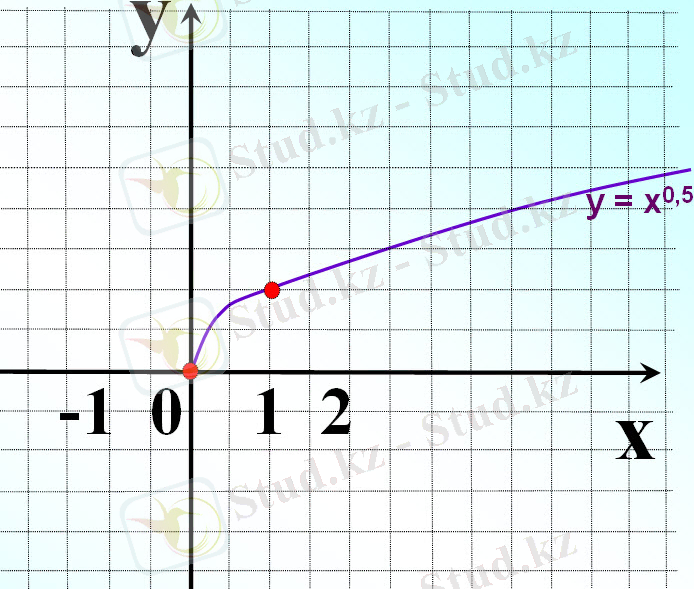

n=2k және n=2k+1 болғанда y=
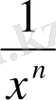 функциясының қасиеттері
функциясының қасиеттері
Тест тапсырмалары
Мына функциялардың қайсысы дәрежелік функцияға жатады:
А)
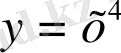 В)
В)
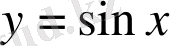 С)
С)
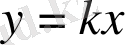 Д)
Д)
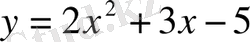 ) Е)
) Е)
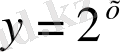
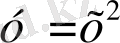 функциясының анықталу облысын кқрсетіңіз:
функциясының анықталу облысын кқрсетіңіз:
А) Натурал сандар жиыны В) Бүтін сандар жиыны
С) Рационал сандар жиыны Д) Нақты сандар жиыны
Е) Теріс емес сандар жиыны
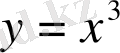 функцияснық графигі қай координаталық ширектерде орналасады:
функцияснық графигі қай координаталық ширектерде орналасады:
А) I және II В) II және IV С) II және III Д) I және III Е) I және IV
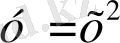 функцияларының мәндерінің облысын көрсетіңіз.
функцияларының мәндерінің облысын көрсетіңіз.
А) Теріс емес сандар жиыны В) Бүтін сандар жиыны
С) Натурал сандар жиыны Д) Нақты сандар жиыны
Е) Рационал сандар жиыны
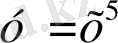 функциясының графигі қандай нүкте арқылы өтеді.
функциясының графигі қандай нүкте арқылы өтеді.
А) (2; 16) В) (-2; 32) С) (3; 243) Д) (-1; 0) Е) (-4; -64)
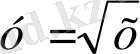 функциясының графигі қай нүкте арқылы өтеді.
функциясының графигі қай нүкте арқылы өтеді.
А) (12; 144) В) (121; 11) С) (121;
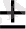 11) Д) (1; 0) Е) (121; 11)
11) Д) (1; 0) Е) (121; 11)
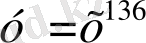 функция графигі қандай координаталық ширектерде орналасқан.
функция графигі қандай координаталық ширектерде орналасқан.
А) I және III В) II және IV С) II және III Д) I және II Е) I және IV
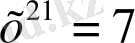 теңдеуінің неше шешімі болатынын анықтандар.
теңдеуінің неше шешімі болатынын анықтандар.
А) жоқ В) екі С) бір Д) үш Е) жеті
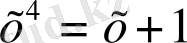 теңдеуінің неше шешімі болатынын анықтандар.
теңдеуінің неше шешімі болатынын анықтандар.
А) жоқ В) екі С) бір Д) үш Е) төрт
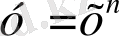 функциясының графигі А(-243; -3) нүктесі арқылы өтетін болса,
функциясының графигі А(-243; -3) нүктесі арқылы өтетін болса,
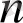 -ді табындар. А)
-ді табындар. А)
 В) 5 С) -5 Д) 3 Е) 0
В) 5 С) -5 Д) 3 Е) 0
 N
N
 )
)
 )
)
 ; 0)
; 0)
 ) аралығында f(x) >0
) аралығында f(x) >0
(-
 ; 0) аралығында f(x) <0
; 0) аралығында f(x) <0
(0; +
 ) аралығында f(x) >0
) аралығында f(x) >0
 N
N
 ; 0)
; 0)
 ( 0; +
( 0; +
 )
)
 ; 0)
; 0)
 ( 0; +
( 0; +
 )
)
 )
)
 ; 0)
; 0)
 ( 0; +
( 0; +
 )
)
 ; 0)
; 0)
 )
)
 ; 0)
; 0)
 ( 0; +
( 0; +
 )
)
 ; 0)
; 0)
 ( 0; +
( 0; +
 ) аралығында f(x) >0
) аралығында f(x) >0
(-
 ; 0) аралығында f(x) <0
; 0) аралығында f(x) <0
(0; +
 ) аралығында f(x) >0
) аралығында f(x) >0
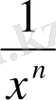 n >1
n >1
 )
)
 )
)
 )
)
 ) аралығында f(x) >0
) аралығында f(x) >0
(-
 ; 0) аралығында f(x) <0
; 0) аралығында f(x) <0
(0; +
 ) аралығында f(x) >0
) аралығында f(x) >0
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz