Пифагор теоремасын дәлелдеудің түрлері

ҚАЗАҚСТАН РЕСПУБЛИКАСЫ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ
Маңғыстау облысы, Ақтау қаласы
<<Мектепке дейінгі шағын орталығы бар №3 жалпы білім беру
орта мектебі>> мемлекеттік мекемесі

Ашық сабақ

Тақырыбы: Пифагор теоремасы

Орындаған: математика пәні мұғалімі
Утегенова Н.Д.

Ақтау- 2014 ж
Пәні: Геометрия Сынып: 8 сынып

Сабақтың тақырыбы: Пифагор теоремасы
Сабақтың мақсаты:
Білімділік: Пифагор теоремасын және оған кері теореманы тұжырымдап,
дәлелдей алып, оларды геометриялық есептерді шығару
барысында қолдану дағдыларын қалыптастыру.
Дамытушылық: Оқушылардың қызығушылық, логикалық іскерліктерін,
абстракциялы ой-өрісін жаңа ұғымдар арқылы кеңейту
Тәрбиелік: Ұқыптылыққа, тиянақтылыққа, мәдениетті сөйлеуге үйрету.
Сабақтың типі: аралас сабақ
Әдісі: түсіндірмелі,сұрақ-жауап тәжірибелік іздену
Түрі: жаңа сабақ
Сабақтың көрнекілігі: Пифагор портреті,сызу құралдары (бұрыштық,
сызғыш), интерактивті тақта, тест тапсырмалары,
тарихи мағлұматтар, слайдтар.

Сабақтың құрылымы:

I. Ұйымдастыру а) сыныптың сабаққа дайындығын тексеру;
б) оқушылардың сабаққа әзірлігін анықтау
II. Қызығушылығын ояту.
1. Барлық қабырғалары тең тіктөртбұрыш (квадрат)
2. Бір бұрышы 90градусқа тең үшбұрыш (тікбұрышты үшбұрыш)
3. Үшбұрыштың перпендикуляр екі қабырғасы(катет)
4. Үшбұрыштың тік бұрышына қарсы жатқан қабырға (гипотенуза)
5.Тікбұрышты үшбұрыштың сүйір бұрышына іргелес жатқан катеттің
гипотенузаға қатынасы (сүйір бұрышының косинусы).
III. Жаңа сабақ
а)Пифагордың өмірбаянымен таныстыру.

Ұлы оқымысты Пифагор б. з. д. 570 жылдары Самос аралында дүниеге келген. Оның әкесі Мнесарх бағалы тастармен айналысқан. Пифагордың анасының есімі сақталмаған. Кейбір деректерге қарағанда оның анасы - Самос аралының негізін қалаушы Анкея тегінің қызы Пифаида. Пифагор ежелгі Грецияда 570 - 500 жж. өмір сүрген. Ол бала кезінен саяхат жасауды армандаған. Пифагор Үндістанда, Египетте, Вавилонда болған. Өзге елдердің ғылыми жетістіктері мен ежелгі мәдениетін зерттеген. Отанына оралғаннан кейін Пифагор аристократия уәкілдерімен жастар үйірмесін ұйымдастырған. Үйірмеге ұзақ сын емтихандардан кейін салтанатпен қабылдаған. Оған енуші әр адам өз мүлкінен безіп, бас тартқан және ілімнің негізін құраушының оқуын құпия сақтауға ант берген. Осылайша Оңтүстік Италияда атаулы "Пифагор мектебі" пайда болды. Пифагоршылар математикалық, философиялық, жаратылыс ғылымдарымен айналысқан. Олармен көп жаңалық ашқан. Пифагор халық көтерілісі кезінде көше шайқасында өлген.

ә)Пифагор теоремасының тарихынан мәлімет беру

Пифагор теоремасының бай тарихы бар. Пифагорға дейін көп уақыт бұрын ол мысырлықтарға, вавилондықтарға, үндістерге, қытай халқына белгілі болған. Үнді халқы "жіп ережесі" деп атап, құрбандық шалатын орын құру үшін пайдаланған. Өзінің осы теореманы дәлелдеу салтанатының құрметіне Пифагор құрбандыққа бұқаны немесе өзгелер айтқандай 100 бұқа шалғаны туралы аңыз әңгімелер немесе өлеңдер жазуға себеп болды. Ежелгі мысырлықтар жер өлшегенде осы"жіп ережесін"былайша қолданған: жіпті түйін салып тең 12 - ге бөлгенде, ұштарын біріктіріп байлаған. Содан кейін қабырғалары 3, 4, 5 бөлікке тең үшбұрыш шығатындай етіп жіпті жердің бетімен керіп тастаған. Сонда үшбұрыштың 5 бөлігі қабырғасына қарсы жатқан бұрышы тік болады.
Қабырғалары 3, 4, 5 сандарымен өрнектелетін тік бұрышты үшбұрыш <<Египет үшбұрышы>> деп аталған. Египеттіктер жер бетінде тік бұрыш салып көрсету үшін, жіпті 12 тең бөлікке бөліп, 3 бөлігінен 1 түйін, онан кейін 4 бөлігінен 1 түйін салып, 2 ұшын түйетін де, сол түйіндерге қазықтар қағып көргенде жер бетінде тік бұрышты үшбұрыш пайда болатын. Мұндай үшбұрыштар көп болатын. Олардың қабырғаларын 5, 12 және 13; 7, 24 және 25 т.с.с сандармен өрнектеген. Осы сандар <<Пифагор сандары>> деп аталады.

б) Теоремамен жұмыс
Теорема:
Тік бұрышты үшбұрыштың гепотенузасының квадраты
катеттерінің квадраттарының қосындысына тең.

Пифагор теоремасын дәлелдеудің түрлері
1.
Берілгені: ▲АВС(∠С=90[0])

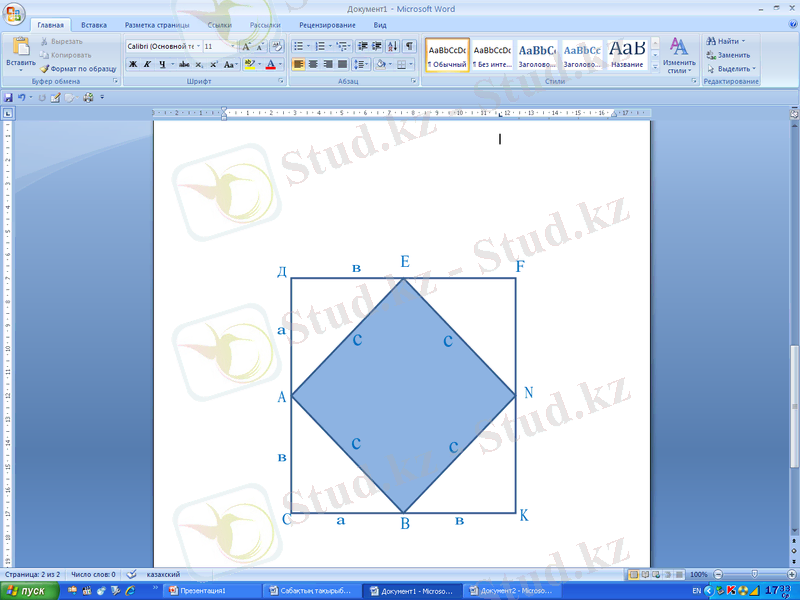Дәлелдеу керек: АВ[2]=АС[2]+СВ[2]

Дәлелдеу:АВ=с, АС=b, СВ=а
Берілген үшбұрышты қабырғасын а+в
квадратқа дейін толықтырайық.
(а+в) S=
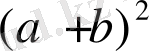
S=.

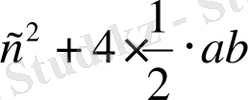Сонда
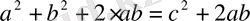, бұдан с2=а2+b2. Теорема дәлелденді.
2. Теореманың қарапайым дәлелдеуі тең бүйірлі үшбұрыш жағдайында қарастырылады. Теореманың өзі де осыдан басталған.
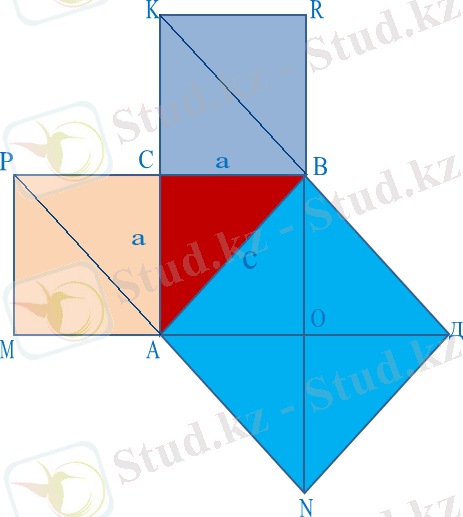Тік бұрышты үшбұрыштың гипотенузасына салынған квадрат катеттеріне салынған квадраттардың қосындысымен тең шамалы.
Теореманың дұрыстығына көз жеткізу үшін тең бүйірлі тікбұрышты үшбұрыштар мозаикасына қарау жеткілікті. Мысалы, ΔABC үшін : АВ гипотенузасына салынған квадрат 4 үшбұрыштан құралған, ал катеттерге салынған квадраттардың әрқайсысы екі үшбұрыштан тұрады. Теорема дәлелденді.

Пифагор теоремасына кері теорема:

Үшбұрыштың бір қабырғасының квадраты қалған екі қабырғасының квадраттарының қосындысына тең болса, онда үшбұрыш тікбұрышты болады.

Арнайы тікбұрышты үшбұрыштар арқылы қорытынды шығады.

d
Пифагор теоремасының қолданылуы: 1. Квадраттың диагоналы:
d2 = 2a2 => d = a√2 a

a
2. d
Тіктөртбұрыштың диагоналы: d2 = a2 +b2=> d =a2+b2
b

a
h
3. Тең қабырғалы үшбұрыштың биіктігі:
h2 =a2 - a24 h2 = 3a24 =>h = a32 а

a2

IV. Жаңа сабақты бекіту, қорытындылау:
а) Фронталды сұрақтар:
1. Ұзындықтары 5, 4, 3-ке тең кесінділер тікбұрышты үшбұрыштың қабырғалары болады деп есептеуге бола ма?
Шешуін, тәжірибе арқылы дәлелдеу
(12 жерінен түйінделіп тұйықталған жіпті пайдаланып, есептеуге болатындығын көрсетеді)
2. Қабырғаларының ұзындықтары 5, 6, 7 болатын үшбұрыш тікбұрышты ма?
(Сызғыштардың шкалаларын пайдаланып мүмкін емес екендігін үш-үштен оқушылар бірігіп көздерін жеткізеді.)

ә) Тест тапсырмасы: (жеке жұмыс, жұптық жұмыс)

Интерактивті тақтада екі нұсқалық есептер орындап, нәтижесін өздері экраннан көре отырып, бірінің жұмысын бірі тексереді, бағалайды.

Тест

1- нұсқа 2-нұсқа
1.

2.

3.

б) Сергіту сәті.

Жауабы:
1-нұсқа 2- нұсқа
1. 12 1. 10
2. 74 2. 32
3. 15 3. 12
4.
в) Есептер шығару:

Жауабы:

1. 17 2. 41
3. 12 4. 53
5. 73

V. Оқушылардың білімін бағалау:
а) сұрақтар қою
б) ауызша есептер беру
в) бір-біріне сұрақтар қойғызу

VI. Үйге тапсырма: §9, №142, №145
а) түсіндіру; б) бағыт-бағдар беру

Қорытынды: Сонымен қорытындылай келе, Пифагор теоремасының қажеттілігі: есептер шығаруда, үлкен құрылыстарда, теоремаларды дәлелдегенде т.т. Сондықтан бұл теореманың қыр - сырын толығырақ әрі тереңірек білу қызығушылық тудырады.