12-жылдық білім беру аясында математика пәнінен құзыреттілікті қалыптастыруға бағытталған тапсырмалар үлгілері (5 және 11-сыныптарға арналған)


12-жылдық білім беру аясында математика пәнінен құзыреттіліктерді қалыптастыруға бағдарланған тапсырмалар үлгісі
Алғысөз
Оқушылардың білім деңгейіне мезгілімен айқын, дәл баға беру олардың білімге құштарлығын арттыруға түрткі болары сөзсіз. Сонымен қатар оның тәрбиелік маңызы да зор. Сол себепті тапсырмалар оқушылардың тек білімінің деңгейі ғана емес, олардың күтілетін нәтижелерге жетудегі әрбір қимылы, яғни әрбір іс-әрекеті тексерілетіндей етіп жасалды. Сонымен қатар төмендегідей ғылыми негіздемеге сүйене отырып, оқушылардың құзыреттіліктің үш деңгейіне жетуге мүмкіндік алуына жағдай жасалды.
- Мазмұны бойынша тапсырмалар оқушылардың:
- математикалық ойлауын;
- математикалық жағдаяттарды ауызша және жазбаша дәйектеу біліктерін;
- проблема қою және оны шешу біліктерін;
- математикалық модель құру, математикалық тілді пайдалану біліктерін дамытуға мүмкіндік жасасуы тиіс.
- Тапсырмаларды түзуде математикалық құзыреттіліктің үш деңгейі ескерілді. Оның біріншісі математикалық фактілерді мазмұндауды, есептеу әдістерін және есептеуді орындауды қамтиды, екіншісі, қойылған міндетті шешу үшін қажетті әртүрлі математикалық тақырыптардан алынған материалдардың байланысын анықтаумен және оны интеграциялаумен сипатталады. Үшінші деңгей жалпылау мен интуицияны қажет ететін математикалық ойлауды талап етеді.
Оқушылардың құзіреттіліктің бірінші деңгейіне жетуін тексеру үшін дәстүрлі оқу есептері пайдаланылды. Екінші деңгей қарапайым өмірлік мәні бар есептер шығару көмегімен жүзеге асырылады. Үшінші деңгейге жетуін тексеру үшін ұсынылған өмірлік жағдаятты өзбетінше «математикаландыру» қажет етілетін күрделі тапсырмалар құрастырылды. Мұнда оқушы жағдаяттағы математика құралдарымен шешілетін негізгі проблеманы анықтайды, соған сәйкес оның математикалық моделін құрады. Одан кейін қойылған математикалық есепті шешу жолдарын ойластырады, математикалық тұжырымдамалардың көмегімен оны шешеді. Бұл әрекет тапсырмада қарастырылған жағдаяттың жеке ерекшеліктерін ескере отырып есеп жауабын тұжырымдаумен аяқталуы қажет.
І тапсырма.
Тақырып: Ең кіші ортақ еселік. 5-сынып.
Тапсырмалар үш бөлімнен тұрады.
І бөлім. Оқушылардың теориялық білімдерін тексеру:
- Берілген натурал сандардың ең кіші ортақ еселігі деп қандай санды атайды?
- Берілген натурал сандардың ең кіші ортақ еселігі қалай табылады?
- Өзара жай сандардың ең кіші ортақ еселігі неге тең?
- Егер берілген натурал сандардың біреуі басқа берілген сандарға бөлінсе, олардың ең кіші ортақ еселігі қалай табылады?
Теориялық жауаптар бес баллдық жүйемен бағаланады.
ІІ бөлім. Ең кіші ортақ еселікті табу бойынша тест алынады.
І нұсқа.
- Берілген сандардың ішінен 12-ге еселік сандарды көрсетіңдер:
- Өзара жай сандар жұбын көрсетіңдер:
- Егерa=73•112•13, b=52•11•132a = 7^{3} \bullet 11^{2} \bullet 13, \ \ \ b = 5^{2} \bullet 11 \bullet 13^{2}болса, aжәнеbсандарының ЕКОЕ-н табыңдар.
- Берілген 10, 15, 20, 45, 105, 135 сандарының ішінен осы сандардан тұратын еселігі ең көп санды таңдап алыңдар.
- ЕКОЕ-і 300-ге тең болатын сандарды табыңдар:
- 42, 60 және 70 сандарын жай көбейткіштерге жіктеп, ең кіші ортақ еселігін табыңдар:
Тест жауаптары да бес баллдық жүйемен бағаланады.
ІІІ тапсырма
Натурал сандардың бөлінгіштігі тақырыбы бойынша оқушылардың логикалық ойлары және практикалық дағдылары тексеріледі. Бұл тапсырмалар неғұрлым күрделірек, дәстүрден тыс есептерді шығаруда алынған білімдерін пайдалануды көздейді.
- Ыңғайлы тәсілмен ауызша есептеңдер:
Жауаптар: (99, 75, 87, 123, 111)
- Алынған нәтижелерді өсу ретімен орналастырыңдар.
(75, 87, 99, 111, 123)
- Заңдылықты анықтап, қатарды үш санға жалғастырыңдар.
(75, 87, 99, 111, 123, 135, 147, 159. )
- Алынған қатардан 11-ге еселік санды көрсетіңдер. (99)
- Алынған қатардан ондықтарының саны бірліктер санынан 2-ге артық санды көрсетіңдер. (75)
- 99 және 75 сандарын салыстырыңдар. Қажетті сұрақтар қойыңдар.
- Мәні 24-ке тең болатын санды өрнек құрастырыңдар.
- 24 және 15 сандарын ауызша жай көбейткіштерге жіктеңдер және ЕҮОБ(24, 15) пен ЕКОЕ(24, 15) табыңдар.
- Жай көбейткіштерге жіктеу жіктеу арқылы ЕҮОБ және ЕКОЕ табу алгоритмдерін тұжырымдаңдар.
- Қандай жағдайлар болуы мүмкін?
- a=2•5•5•11, b=2•2•3•5•7a = 2 \bullet 5 \bullet 5 \bullet 11, \ \ \ b = 2 \bullet 2 \bullet 3 \bullet 5 \bullet 7
- aсанына еселік санға мысал келтіріңдер.
- bсанына еселік саннға мысал келтіріңдер
- aжәнеbсандарының ЕКОЕ-н табыңдар.
Бұл тапсырмалар он баллдық жүйемен бағаланады
18 - 20 балл бағасы «5»
15 - 17 балл бағасы «4»
12 - 14 балл бағасы «3»
12 баллдан кем - «2»
І тапсырма.
Тақырып: Көрсеткіштік функция. 11-сынып.
Тасырмалар үш бөлімнен тұрады.
І бөлім. Оқушылардың теориялық білімдерін тексеру:
- Көрсеткіштік функцияның анықтамасын беріңдер.
- Көрсеткіштік функцияның негізгі қасиеттерін тұжырымдап беріңдер.
- Көрсеткіштік теңдеудің анықтамасын беріңдер.
- Көрсеткіштік теңдеулерді шешу тәсілдерін және олардың алгоритмдерін тұжырымдап беріңдер.
- Көрсеткіштік теңсіздікке анықтама беріңдер.
- Көрсеткіштік теңсіздіктерді шешу үшін қолданылатын тұжырымдарды беріңдер.
Теориялық жауаптар бес баллдық жүйемен бағаланады.
ІІ бөлім. Көрсеткіштік функцияның қасиеттері және графиктері бойынша тест алынады.
І нұсқа
- Берілген функциялардың ішінен көрсеткіштік функцияларды таңдаңдар:
А)
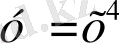 ; Б)
; Б)
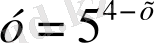 ; В)
; В)
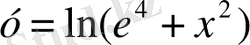 ; Г)
; Г)
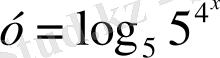 ;
;
Д)
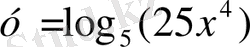 ; Е)
; Е)
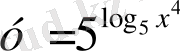 ; Ж)
; Ж)
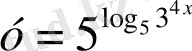 ;
;
З)
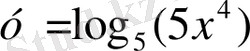 ; И)
; И)
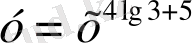 ; К)
; К)
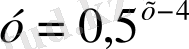 .
.
2. Анықталу облысы болатын көрсеткіштік функциялар
A)
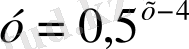 ; Б)
; Б)
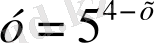 ; В)
; В)
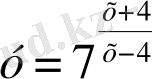 ; Г)
; Г)
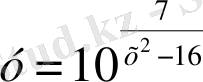 ; Д)
; Д)
 ; Е)
; Е)
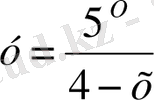 .
.
3. Көрсеткіштік функциялардың қайсылары өспелі болады?
1)
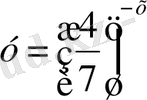 ; 2)
; 2)
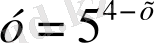 ; 3)
; 3)
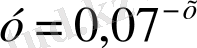 ; 4)
; 4)
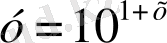 ; 5)
; 5)
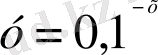 ; 6)
; 6)
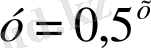 ; 7)
; 7)
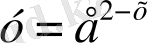 ; 8)
; 8)
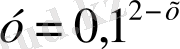 ; 9)
; 9)
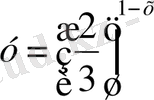 ; 10)
; 10)
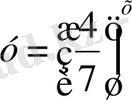 .
.
A) 1, 3, 4, 5, 7; Б) 1, 3, 4, 5, 8, 9; В) 2, 4, 5, 6, 8, 10; Г) 2, 5, 6, 10;
Д) 2, 6, 7, 10; Е) 2, 3, 5, 6, 9; Ж) 3, 4, 7, 8, 10; З) 1, 3, 4, 6; 8, 9.
4. Функциялар графиктерінің қай жұптары абсциссалар осьтеріне қарағанда симметриялы болады?
1)
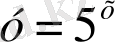 ; 2)
; 2)
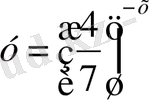 ; 3)
; 3)
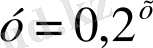 ; 4)
; 4)
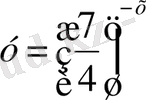 ;
;
5)
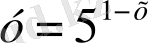 ; 6)
; 6)
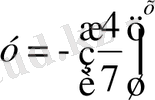 ; 7)
; 7)
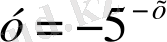 ; 8)
; 8)
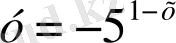 .
.
А) 1, 7; Б) 5, 8; В) 1, 5; Г) 1, 3; Д) 2, 6; Е) 3, 7; Ж) 4, 6; З) 2, 4.
5. Қай функциялардың графиктері беттеседі?
1)
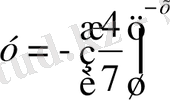 ; 2)
; 2)
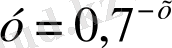 ; 3)
; 3)
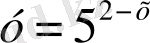 ; 4)
; 4)
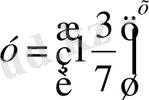 ; 5)
; 5)
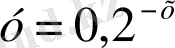 ; 6)
; 6)
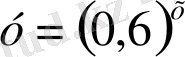 ; 7)
; 7)
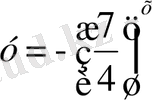 ; 8)
; 8)
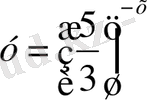 ; 9)
; 9)
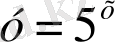 ; 10)
; 10)
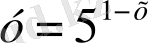 .
.
А) 4, 7; Б) 3, 10; В) 2, 4; Г) 3, 5; Д) 5, 9; Е) 1, 7; Ж) 5, 10; З) 6, 8,
6.
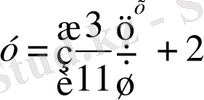 функциясының мәндері жиынын көрсетіңдер:
функциясының мәндері жиынын көрсетіңдер:
А)
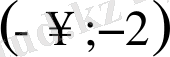 ; Б)
; Б)
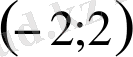 ; В)
; В)
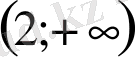 ; Г)
; Г)
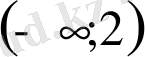 ; Д)
; Д)
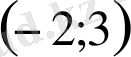 ; Е)
; Е)
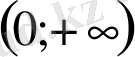 ; Ж)
; Ж)
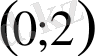 .
.
ІІ нұсқа
- Берілген функциялардың ішінен көрсеткіштік функцияларды таңдаңдар:
- Анықталу облысыx∈(−∞; 5) ∪(5; +∞) x \in ( - \infty; 5) \cup (5; + \infty) болатын көрсеткіштік функциялар
3. Көрсеткіштік функциялардың қайсылары кемімелі болады?
1)
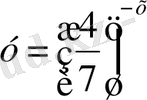 ; 2)
; 2)
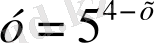 ; 3)
; 3)
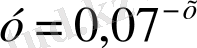 ; 4)
; 4)
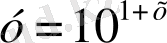 ; 5)
; 5)
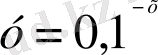 ; 6)
; 6)
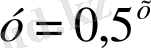 ; 7)
; 7)
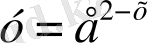 ; 8)
; 8)
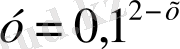 ; 9)
; 9)
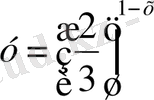 ; 10)
; 10)
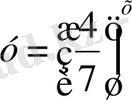 .
.
A) 1, 3, 4, 5, 7; Б) 1, 3, 4, 5, 8, 9; В) 2, 4, 5, 6, 8, 10; Г) 2, 5, 6, 10;
4. Функциялар графиктерінің қай жұптары ординаталар осьтеріне қарағанда симметриялы болады?
1)
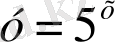 ; 2)
; 2)
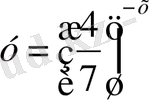 ; 3)
; 3)
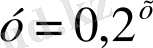 ; 4)
; 4)
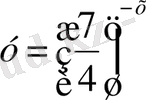 ;
;
5)
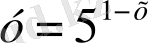 ; 6)
; 6)
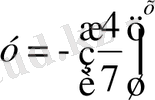 ; 7)
; 7)
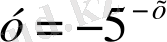 ; 8)
; 8)
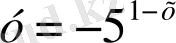 .
.
А) 1, 7; Б) 5, 8; В) 1, 5; Г) 1, 3; Д) 2, 6; Е) 3, 7; Ж) 4, 6; З) 2, 4.
5. Қай функциялардың графиктері беттеспейді?
1)
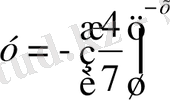 ; 2)
; 2)
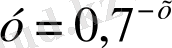 ; 3)
; 3)
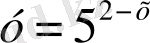 ; 4)
; 4)
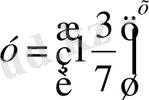 ; 5)
; 5)
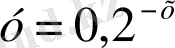 ; 6)
; 6)
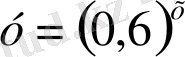 ; 7)
; 7)
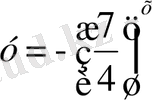 ; 8)
; 8)
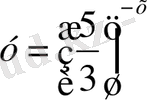 ; 9)
; 9)
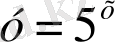 ; 10)
; 10)
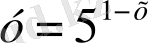 .
.
А) 4, 7; Б) 3, 10; В) 2, 4; Г) 3, 5; Д) 5, 9; Е) 1, 7; Ж) 5, 10; З) 6, 8,
6.
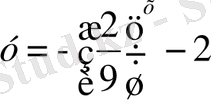 функциясының мәндері жиынын көрсетіңдер:
функциясының мәндері жиынын көрсетіңдер:
А)
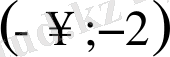 ; Б)
; Б)
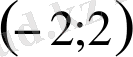 ; В)
; В)
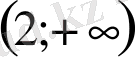 ; Г)
; Г)
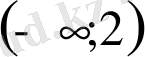 ; Д)
; Д)
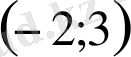 ; Е)
; Е)
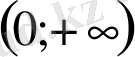 ; Ж)
; Ж)
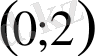 .
.
Тест жауаптары да бес баллдық жүйемен бағаланады.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz