Stud.kz
Сабақ жоспары :: Әртүрлі

Оқушылардың квадрат теңдеулерді Виет теоремасы арқылы шешу дағдыларын жетілдіру

Виет теоремасы

Сабақтың тақырыбы: Виет теоремасы .

Сабақтың мақсаты : 1) Оқушылардың квадрат теңдеулерді Виет теоремасы арқылы шешу дағдыларын жетілдіру.

2) Оқушылардың ойларын жеткізе білуін қалыптастыру және ой-өрісін дамыту.

3) Оқушыларды ұйымшылдыққа, ұқыптылыққа, дәлдікке тәрбиелеу.

Сабақтың өту әдісі : Деңгейлеп, саралап оқыту.

Сабақтың түрі : Біліктілік пен дағдыны игеру және қалыптастыру сабағы.

Сабақтың көрнекілігі : Плакатта жазылған есептер, карточкалар, кестелер.

Сабақтың барысы : І. Ұйымдастыру кезеңі.

ІІ. Үй тапсырмасын тексеру.

№ 148

1) х 2 - 5х + 6 = 0 5) х 2 - 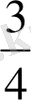х + = 0 9) х 2 -2х + 1 = 0

2) х 2 - 8х + 12 = 0 6) х 2 - 0, 6х + 0, 08 = 0 10) х 2 - 5х = 0

3) х 2 - 8х + 15 = 0 7) х 2 - 4х + 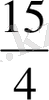= 0 11) х 2 - х = 0

4) х 2 - 3х + 2 = 0 8) х 2 - х + 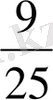= 0 12) х 2 - 10х + 25 = 0

ІІІ. Үй тапсырмасын қорытындылау.

х 1 + х 2 = - p, х 1 х 2 = q Виет теоремасын қолдану арқылы квадрат теңдеуді х 2 + pх + q = 0

түрінде жаздық.

ІҮ. Сабақтың құрылымы:

Бірінші деңгей - танымдық деңгей (ауызша сұрақтар)

  1. Квадрат теңдеудің анықтамасын кім айтады?
  2. Қандай теңдеулер толымсыз квадрат теңдеулер деп аталады?
  3. Қандай теңдеулер келтірілген квадрат теңдеулер деп аталады?
  4. Квадрат теңдеулерді шешудің формуласы қалай жазылады?
  5. Дискриминантты табудың үш жағдайы
  6. Виет теоремасы қалай жазылады?

Екінші деңгей - алгоритмдік деңгей ( тест)

«Зерде» ойыны. Мақалдардың жалғасын тап.

А) х 2 - 8х + 7 = 0

х 1 + х 2 = 8, х 1 х 2 = 7

х 1 = 1, х 2 = 7

Жеті рет өлшеп, ( бір рет кес)

ә) х 2 - 11х + 10 = 0

х 1 + х 2 = 11, х 1 х 2 = 10

х 1 = 1, х 2 = 10

Бір тал кессең, ( он тал ек)

Б) х 2 - 9х + 8 = 0

х 1 + х 2 = 9, х 1 х 2 = 8

х 1 = 1, х 2 = 8

Жігіт бір сырлы, ( сегіз қырлы)

В) х 2 - 70х + 1200 = 0

х 1 + х 2 = 70, х 1 х 2 = 1200

х 1 = 30, х 2 = 40

Ұлға 30 үйден, (қызға 40 үйден) тыю.

Үшінші деңгей - эвристикалық деңгей. Әр есептің жауабын таңдау.

А) х 2 - 2х - 35 = 0 1) х 1 = 1, х 2 = 7

Ә) х 2 + 4х + 3 = 0 2) х 1 = -5, х 2 = 3

Б) х 2 - 8х + 7 = 0 3) х 1 = -1, х 2 = -3

В) х 2 + 10х - 11 = 0 4) х 1 = -5, х 2 = 7

Г) х 2 + 2х - 15 = 0 5) х 1 = -11, х 2 = 1

Жауабы: А - 4, Ә - 3, Б - 1, В - 5, Г - 2.

Төртінші деңгей - шығармашылық деңгей.

  1. Күрделі: 2х ( 5х - 7) = 2х2- 5

( х + 4) 2 = 4х 2 - 5

  1. Орташа: 5х2+ 4х - 1 = 023х2- 22х + 1 = 0
  2. Жеңіл: 3х2+ 5х - 2 = 0

9х 2 - 6х + 1 = 0

Ү. Сабақты қорытындылау. Квадрат теңдеуді шешудің әр түрлі әдістеріне тоқталу.

ҮІ. Үйге тапсырма беру: № 160

ҮІІ. Оқушылар білімін бағалау.

Пән мұғалімі: Омарова Дина


Ұқсас жұмыстар
Виет теоремасы. Сабақтың тақырыбы
Квадрат теңдеулерді шешу
Квадрат теңдеулерді Виет теоремасы арқылы шешу
Квадрат теңдеулерді шешу тәсілдері
Виет теоремасы
Виет теоремасы туралы
АЛГЕБРАЛЫҚ ТЕҢДЕУЛЕР ЖӘНЕ ОЛАРДЫ ШЕШУ ӘДІСТЕРІ
Квадрат теңдеулерді шешудің әдістері
Квадрат теңдеулер түрлері
Квадрат теңдеуді коэффициенті бойынша шешу
Пәндер

Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.

google play appstore

instagram tiktok

Ақпарат

Қосымша


Email: info@stud.kz



Реферат Курстық жұмыс Диплом Материал Диссертация Практика Презентация Сабақ жоспары Мақал-мәтелдер 1‑10 бет 11‑20 бет 21‑30 бет 31‑60 бет 61+ бет Негізгі Бет саны Қосымша Іздеу Ештеңе табылмады :( Соңғы қаралған жұмыстар Қаралған жұмыстар табылмады Тапсырыс Антиплагиат Қаралған жұмыстар kz