Кітапханадағы әдеби кітаптардың саны қанша

5 сынып математика.
Тоқсандық бақылау жұмысы.
1-ші нұсқа
1. Бөлшектерді процентпен жазыңдар: 0,2; 0,8; 0,75; 2,3.
2. Кітапханада 35 000 кітап бар. Оның 22%-і әдеби кітаптар. Кітапханадағы әдеби кітаптардың саны қанша?
3. Бензин құйған соң біраз жүргеннен кейін машинаның бензин құятын багында 25 л бензин қалды. Бұл алғашында құйылған бензиннің 50% -індей. Машинаның бензин құятын багында алғашында неше литр бензин болған?
4. Сынып оқушыларының 40%-і шаңғы тебе біледі. Қалғандары конькимен сырғанай алады. Сынып оқушыларының шаңғы тебе білетіндерінің және конькимен сырғанай алатындарының дөңгелек диаграммасын салыңдар.
5. Есепте: 365,5 : (6,2 - 4,5) * 0,01 + 1,85

2-ші нұсқа

1. Бөлшектерді процентпен жазыңдар:
0,5; 0,4; 0,15; 1,25.

2. Мектепте барлығы 1 500 оқушы бар. Оның 42%-і ұл балалар. Мектепте қанша ұл бала бар?
3. Оқушы кітаптың 124 бетін оқыды. Бұл кітаптың барлық бетінің 62% -і. Кітапта неше бет бар?
4. Мектеп кітапханасында кітаптардың 80%-і оқулықтар, қалғаны әдеби кітаптар. Мектеп кітапханасындағы кітаптардың дөңгелек диаграммасын салыңдар.

5. Есепте: 408,8 : (6,3-5,18)*0,01 + 1,35

5 сынып математикадан жылдық бақылау жұмысы.
1-ші нұсқа
1.Амалдарды орындаңдар:
А)
Б)
2.Теңдеуді шешіңдер:
3. Бір қорапта үш түсті 120 қарындаш бар. Қарындаштардың бөлігі қара, ал бөлігі ақ. Қызыл қарындаштардың санын табыңыз.
4. Әсеттің массасы 35 кг. Адам массасының 65%-і су. Әсеттің денесінде неше кг су бар?
5. Бөлшекті қысқартыңдар:
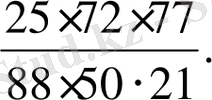
6. . ВОС жазыңқы бұрышының О төбесінен ОD сәулесі жүргізілді. Сонда <ВОD =1250 . DОС бұрыштарының градустық өлшемін тап.

2-ші нұсқа.
1.Амалдарды орындаңдар:
А)
Б )
2.Теңдеуді шешіңдер:
3.Матаның жартысы, одан кейін қалған бөліктің жартысы сатылды. Осыдан кейін 0,5м мата қалды. Бастапқыда неше метр мата болғанын табыңыз.

4 . Бүлдіргеннің 6%-і құмшекер болады. 27 кг. бүлдіргеннен неше кг. құмшекер шығады?
5. Бөлшекті қысқартыңдар:
6. АОВ жазыңқы бұрышының төбесі арқылы ОС сәулесі жүргізілді. < AOC = 1300 ; СОВ бұрышының градустық өлшемін тап.

6 сынып математика
Тоқсандық бақылау жұмысы.
1-ші нұсқа.
1.Есептеңдер:
2. функциясының болғандағы тің сәйкес мәнін тапбыңыз.
3.функциясының графигінің абциссалар осімен қиылысу нүктесінің координаталарын табыңыз.
4. Теңдеулер жүйесін алмастыру тәсілімен шешіңдер:х+у=132х-у=12,5
5.Теңдеулер жүйесін қосу тәсілімен шешіңдер:х-6у=175х+6у=13
6.Үш дәптер мен бес блокнотқа 49 теңге төленді.Егер екі дәптер мен үш блокноттан 1 теңге қымбат болса, онда дәптер мен блокноттың жеке-жеке бағалары қанша?

2-ші нұсқа.
1.Есептеңдер:
2.функциясының болғандағы х-тің мәнін табыңыз.
3. функция графигінің ординаталар осімен қиылысу нүктесінің координаталарын табыңыз.
4. Теңдеулер жүйесін алмастыру тәсілімен шешіңдер:х+у=63х-5у=2
5.Теңдеулер жүйесін қосу тәсілімен шешіңдер:2х+11у=1510х-11у=9

6. Турбазадағы шатырлар мен үйлердiң жалпы саны 25.Әр үйде 4 адам, ал әр шатырда 2 адам тұрады. Турбазада барлығы 70 адам демалып жатқандығы белгiлi болса онда қанша үй және қанша шатыр бар екендiгiн табыңыз.

6 сынып математика Жылдық бақылау жұмысы.
1-ші нұсқа
1.Амалдарды орындаңдар:
2.Теңдеуді шешіңдер:
3. Теңсіздікті шешіңіз:
4. Өрнекті ықшамдаңыз:
5. және функциялар графиктерінің қиылысу нүктесінің координаталарын табыңыз.

6. 160 м - лiк канализация құрылысына 150 керамикалық трубалар қолданылды. Трубалардың ұзындығы 800 мм және 1200 мм едi. Трубалардң әртүрiнен қаншадан алынып едi ?

2-ші нұсқа.
1.Амалдарды орындаңдар:
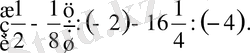
2. Теңдеуді шешіңіз:

3. Теңсіздікті шешіңіз:
4. Өрнекті ықшамдаңыз:
5. және функциялары графиктерінің қиылысу нүктесін табыңыз.

6. Аудандары 80 га және 120 га тең болатын екi участоктен барлығы 7200 ц астық жиналды. Бiрiншi участоктың әрбiр 3 га жиналған астықтың мөлшерi екiншi участоктың 2 га жиналган астық мөлшерiнен 10 ц-ге артық деп алып, әр участоктың 1 га-дан қаншадан астық жиналғанын табыңыздар.

7 сынып тоқсандық бақылау жұмысы.
1-ші нұсқа.
1. Бөлшекті қысқартыңыз: а) ; б)
2.. Өрнекті ықшамдаңыз:
3. Өрнекті ықшамдаңыз:
4. Өрнекті ықшамдаңыз:
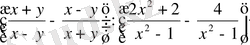
5.Бірлікке дейін дөңгелектеп салыстырмалы қателегін пайызбен өрнектеңдер: 45,62
6. Қораптағы 20 тетіктің 15 - і боялған.Қораптан құрастырушының кездейсоқ алынған тетіктің боялған болу ықтималдығын табыңдар.

2- ші нұсқа.
1. Бөлшекті қысқартыңыз:а) ; б)
2. Өрнекті ықшамдаңыз:
3. Өрнекті ықшамдаңыз:
4. Өрнекті ықшамдаңыз:
5.Бірлікке дейін дөңгелектеп салыстырмалы қателегін пайызбен өрнектеңдер: 13,29
6.Қорапта 10 ақ, 10 қара түсті шарлар бар.Қораптан кездейсоқ алынған шардың ақ болу ықтималдығын табыңдар.

7 сынып жылдық бақылау жұмысы.
1-ші нұсқа
1.Өрнектің мәнін табыңыз:
2.Өрнекті ықшамдаңыз:
3. Бөлшекті қысқартыңыз:
4. Өрнекті ықшамдаңыз:
5. Теңдеуді шешіңіз:
6.Функцияның графигін салыңдар: у=-12x2

2-ші нұсқа.
1.Өрнектің мәнін табыңыз:
2. Өрнекті ықшамдаңыз:
3. Бөлшекті қысқартыңыз: .
4. Өрнекті ықшамдаңыз:
5. Теңдеуді шешіңдер : 4x2-2х-12=15;
6.Функцияның графигін салыңдар: у=13x3

8 сынып тоқсандық бақылау жұмысы.
1-ші нұсқа
1.Теңсіздікті шешіңіз:(x+3)(x+2)(1-x) 0
2.Теңсіздікті шешіңіз:
3.Теңсіздікті график арқылы шешіңдер:

4. көбейтіндісі қандай аралықта теріс болады ?
5.Тиын екі рет тасталды.Тиынның кем дегенде бір рет елтаңба жағымен түсу ықтималдығын анықтаңдар.

2-ші нұсқа.
1.Теңсіздікті шешіңіз(x+2)(x-1)(x-3)>0 .
2. Теңсіздікті шешіңіз:
3. Теңсіздікті график арқылы шешіңдер: -x2 -5x + 6 0

4 . -3х2 + 6х + 9 > 0 теңсіздігінің ең үлкен бүтін шешімін табыңыз.
5. Қалтадағы 15 асықтың 10 боялған.Қалтадан кездейсоқ алынған асықтың боялған болу ықтималдығын табыңдар.

8 сынып жылдық бақылау жұмысы.
1-ші нұсқа
1. Есептеңдер:
2. Өрнекті ықшамдап , оның мәнін табыңдар:
3. Теңдеуді шешіңдер:
4. Теңдеуді шешіңдер:
5.Теңсіздікті шешіңдер:
6. Екi санның қосындысы 21, ал олардың көбейтiндiсi 90. Осы сандарды табыңдар.

2-ші нұсқа.
1. Есептеңдер:
2. 2. Өрнекті ықшамдап , оның мәнін табыңдар:
3. Теңдеуді шешіңдер:
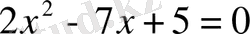
4. Теңдеуді шешіңдер:
5.Теңсіздікті шешіңдер:
6. Бір сан екiншісінен 4-ке артық. Ал олардың квадраттарының айырмасы 56-ға тең. Осы сандарды табыңдар.

9 сынып тоқсандық бақылау жұмысы.
1-ші тоқсан.
1. Есептеңіз: sin70∙ cos230+ sin230∙ cos70
2. Өрнекті ықшамдаңыз:
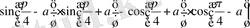
3. Өрнекті ықшамдаңыз:
4. Есептеңіз: 6(sin6a+cos6a), егер cos2a =
5.Шахмат турниріне 8 ойыншы қатысты және әр шахматшы өзгелермен бір-бір ойыннан ойнады.Турнирде барлығы неше партия ойналды?

2-ші тоқсан
1. Есептеңіз : sin640 cos 260+cos640sin 260-sin 300
2. Өрнекті ықшамдаңыз : cos 0,3
3. Өрнекті ықшамдаңыз:
4. Есептеңіз: 125(cos8a-sin8a), егер cos2a = 0,8
5. 5 оқушыны 5 орындыққа неше түрлі тәсілмен отырғызуға болады?

9 сынып математикадан жылдық бақылау жұмысы.
1-ші нұсқа.
1.Теңдеулер жүйесін шешіңдер:х+4у=18x2+у2=20
2. Ықшамдаңыз:
3.Арифметикалық прогрессия аn=6n+2 формуласымен берілген. Прогрессияның алғашқы он алты мүшесінің қосындысын табыңыз.
4. Мүшелерi оң өспелi геометриялық прогрессияның бiрiншi және төртiншi мүшелерiнiң көбейтiндiсi 27, ал екiншi мен үшiншi мүшелерiнiң қосындысы 12 тең. Екiншi мен бесiншi мүшелерiнiң қосындысын табыңыз.
5. 22.Өрнекті ықшамдаңыз:
6. Жедел поезд семафор алдында 16 минут тоқтатылған. Кестеден шығып қалмау үшiн, ол келесi 80 км аралықты жоспарлағаннан 10 км/сағ артық жылдамдықпен жүрген.Поездың кесте бойынша жылдамдығын табыңыз.

2-ші нұсқа.
1.Теңдеулер жүйесін шешіңдер: 2х+у=44x2+у2=40
2. Арифметикалық прогрессияның a = 11, d = 8, n = 17 екендігі белгілі. Прогрессияның n - ші мүшесі мен алғашқы n мүшесінің қосындысын табыңыз.
3. Ықшамдаңыз:
4. Мүшелері оң геометриялық прогрессияның екінші мүшесі 81, ал үшінші мен төртінші мүшелерінің қосындысы 36-ға тең. Прогрессияның бірінші мен бесінші мүшелерінің айырмасын табыңыз.
5. 23. Өрнекті ықшамда :
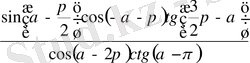
6. Қайық 12 км/сағ жылдамдықпен бір айлақтан екiнші айлаққа қарай шықты. Жарты сағаттан кейiн сол бағытта 20 км/сағ жылдамдықпен пароход шықты. Егер пароход қайықтан 1,5 сағат бұрын келсе, онда айлақтар арасы қанша?

10 сынып тоқсандық бақылау жұмысы.
1-ші нұсқа.

1.[-2; 2]- де y = x3 - 3x2 + 3x + 2 функциясының ең үлкен мәнін табыңыз
2. Сынып оқушы3.1. у = х[2] -4х+3 функциясының :
а) нөлдерін ;
б) өсу аралықтарын;
в) кему аралықтарын анықта.
3.Мектеп оқушыларының шахмат турнирiнде 253 партия ойналды. Әр оқушы қалған ойыншылардың әрқайсысымен бiр партиядан ойнады. Сыныпта қанша оқушы болғаны?

4.Ньютон биномын қолданып жақшаны ашыңдар: a+b10
5. Есептеңдер:С124

2-ші нұсқа.

1.f(x) = 3x5-5x3+1функциясының [-2;2] кесіндісінде ең үлкен және ең кіші мәнін табыңыз.
2 . у = -х[2] +5х функциясының :
а ) нөлдерін ;
б ) өсу аралықтарын
в ) кему аралықтарын анықтаңыз
3 . Мектеп бітірушілер бір - біріне фотосуреттерін сыйлайды. Егер 870 сурет алмастырылған болса, мектеп бітірушілер саны қанша болғаны?
4. m+n11 Ньютон биномын қолданып жақшаны ашыңдар.
5.Есептеңдер: С145

10 сынып жылдық бақылау жұмысы
1-ші нұсқа.
1.Функцияның анықталу облысын табыңдар: у=3х+1-2
2. Теңдеуді шешіңдер: а)2sinх-1=0 б)
3. Теңсіздікті шешіңіз: 2cos2x+5cosx + 2
4. Абсциссасы x0=2 нүктесiнде f(x)=1-2x2 функциясының графигiне жүргiзiлген жанаманың теңдеуiн жаз.
5. y = 3sin2x + 2cos2 x функциясының ең кіші мәнін табыңыз.
6. 25қушының ішінен екі кезекшіні неше түрлі тәсілмен таңдап алуға болады?

2-ші нұсқа.
1.Функцияның анықталу облысын табыңдар: у=x2-4
2. Теңдеуді шешіңдер: а) 2cosх-3=0 б).
3. Теңсіздікті шешіңіз: 2 sin2x-7sinx+3>0
4. Абсциссасы х0=-1 нүктесiнде f(x)=-x2-4x+2 функциясыны графигiне жүргiзiлген жанаманың теңдеуiн жазыңыз.
5. [0; ] - де y = функциясының ең үлкен мәнін табыңыз.
6.Шахмат тақтасының қара түсті торларына бес дойбы тастарын неше түрлі тәсілмен қойып шығуға болады ?

11 сынып тоқсандық бақылау жұмысы.

1.Теңдеуді шешің:
2. a параметрінің әрбір мәнінде теңдеуді шешіңдер :x2+ax+36=0
3. Теңсіздікті шешіңіз:
4. Теңсіздіктер жүйесін шешіңдер :
5. Теңдеуді шешіңіз:
6.Теңдеуді шешіңдер: Сх3+Сх4Сх+12=11

2-ші нұсқа
1.Теңдеуді шешіңіз:
2.a параметрінің әрбір мәнінде теңдеуді шешіңдер : x-ax-3
3. Теңсіздіктi шешіңдер:
4. Теңсіздіктер жүйесін шешіңдер:

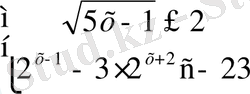
5. Теңдеуді шешіңіздер: ;
6. Теңдеуді шешіңдер: Сх+13-Сх2Сх2=11

11 сынып Жылдық бақылау жұмысы:
1-ші нұсқа
1. Мына функциялардың алғашқы функцияларының жалпы түрін табыңдар:
a) fx=sinx+cosx
b) fx=x2+3x-5
2. Теңдеулер жүйесін шешіңдер: х-у=4х-у=16
3. Өрнектің мәнін табыңдар:а) 81-0,75+125-34-132-35;
ә) log64+log69+log46∙log62+5log52
4. Интегралды есептеңдер: 142-х38dx;
5.Теңдеуді шешіңіз: .
6. Теңсіздікті шешіңдер:

2-ші нұсқа.
1.Мына функциялардың алғашқы функцияларының жалпы түрін табыңдар :
a) fx=5cosx+3sinx b) x=12x3-1x2 ;
2. Теңдеулер жүйесін шешіңдер:х+у=8х-у=32
3. Өрнектің мәнін табыңдар: а)9∙3-2+425-2:100+112
ә)8114-12log94+25log1258∙49log72
4.Интегралды есептеңдер: 4111х+5dx;
5. Теңдеуді шешіңіз:

6. Теңсіздікті шешіңіз:

Годовая контрольная работа. 11 класс
Вариант 1
4. Найти общий вид для заданных функций:
a) fx=sinx+cosx
b) fx=x2+3x-5
5. Решить системы уравнений: х-у=4х-у=16
6. Найти значения выражений :а) 81-0,75+125-34-132-35;
ә) log64+log69+log46∙log62+5log52
4. Вычислить : 142-х38dx;
5 Решить уравнения: .
6. Решить неравенства:
Вариант 2
1. Найти общий вид для заданных функций :
a) fx=5cosx+3sinx b) x=12x3-1x2 ;
2. Решить системы уравнений :х+у=8х-у=32
3. Найдите значения выражений : а)9∙3-2+425-2:100+112
ә)8114-12log94+25log1258∙49log72
4.Вычислить: 4111х+5dx;
5. Решите уравния:

6. Решите неравенства:

Итоговая контрольная работа.
11 класс IY четверть
Вариант 1
1.Реешить уравнения:
2. При каких значениях a уравнения x2+ax+1=0 и x2+x+a=0 имеют общий корень
3. Решить неравенства :
4. Решить системы неравенств :
5. Решить уравнения:
6.Решить уравнения: Сх3+Сх4Сх+12=11

Вариант 2
1. Решить уравнения :
2.Найти коэффициенты уравнеия x2+px+q=0 при условий, что разность корней уравнения равна 5 , а разность их кубов равна 35
3. Решить неравенства :
4. Решить системы неравенств :

5. Решить уравнения : ;
6. Решить уравнения : Сх+13-Сх2Сх2=11

Итоговая контрольная работа.
9 класс IY четверть
Вариант 1

1. Вычислить: sin70∙ cos230+ sin230∙ cos70
2. Упростите выражения:
3. Упростите :
4. Вычислить : 6(sin6a+cos6a), егер cos2a =
5.Участники шахматного турнира играют в зале, где имеются 8 столиков.Сколькими способами можно расположить шахматистов, если исвестны участники всех партий?

Вариант 2
1. Вычислите : sin640 cos 260+cos640sin 260-sin 300
2. Упростить выражения : cos 0,3
3. Упростить выражения:
4. Вычислить: 125(cos8a-sin8a), егер cos2a = 0,8
5. Сколькими способами можно выбрать трех дежурных из группы в 20 человек ?

Годовая контрольная работа. 9 класс
Вариант 1
1.Решить системы уравнений:х+4у=18x2+у2=20
2. Упростите:
3.Найти первый и пятый члены геометрической прогресий, если известно, что знаменатель ее равень 3, а сумма шестий ее первых членов равна 1820
4. Сумма третьего и девятого членов арифметической прогрессий равна 8.Найтий сумму первых 11 членов этой прогресий.
5. Упростите :
6. Товарный поезд был задержан в пути на 12 мин , а затем на растоянии 60 км наверстал потрянное времия , увеличив скорость на 15 км/ч .Найти первоначальную скорость поезда.
Вариан 2
1.Теңдеулер жүйесін шешіңдер: 2х+у=44x2+у2=40
2.Сумма первого и пятого членов арифметической прогрессий равна 53 , а произведение третьего и четвертого ее членов равно 6572 . Найти сумму семнадцати первых членов этой прогрессий.
3. Упростить:
4. Произведение первых трех членов геометрической прогресии равно 1728 ,а их сумма равна 63.Найти первый член и знаменатель этой прогресии.
5. Упростите :
6. Мотоциклист задержался у шлагбаума на 24 мин. Увеличив после этого свою скорость на
10 км/ч , он наверстал опоздание на перегоне в 80 км.Определить скорость мотоциклиста до задержки.

Годовая контрольная работа. 7 класс
Вариант 1
1.Вычислите:

2.Упростите выражение:
3. Сократите дробь:
4. Упростите дробь:
5. Решите уравнение:
6.Постройте график функций: у=-12x2

Вариант 2
1. Вычислите :
2. Упростите выражение:
3. Сократите дробь: .
4. Упростите выражение :
5. Решите уравнение : 4x2-2х-12=15;
6.Постройте график функций: у=13x3

Итоговая контрольная работа.
7 класс IY четверть
Вариант 1
1. Сократите дробь: а) ; б)
2 .Упростите выражение:
3 .Упростите выражение.:
4 .Упростите выражение .:
5.Длина карандаша измерена линейкой с миллиметровыми делениями. Измерение показало 17,9 см. Какова предельная относительная погрешность этого измерения?
6. У мамы 2 яблока и 3 груши. Каждый день в течение 5 дней подряд она выдает по одному фрукту. Сколькими способами это может быть сделано?
2- ші нұсқа.
1. Сократите дробь :а) ; б)
2. Упростите выражение :
3. Упростите выражение :
4. Упростите выражение :
5. Цилиндрический поршень имеет около 35 мм в диаметре. С какой точностью нужно его измерить микрометром, чтобы предельная относительная погрешность составляла 0,05%?
6. В шахматном турнире принимали участие 15 шахматистов, причем каждый из них сыграл только одну партию с каждым из остальных. Сколько всего партий было сыграно в этом турнире?

Итоговая контрольная работа.
8 класс. IY четверть
Вариант 1

1.Решите неравенство :(x+3)(x+2)(1-x) 0
2.Решите неравенство:
3.Решите неравенство графическим способом :

4. при каких значениях х поризведение принимает только отрицательные значения ?
5. В группе 9 человек. Сколько можно образовать разных подгрупп при условии, что в подгруппу входит не менее 2 человек?

Вариант 2
1. Решите неравенство (x+2)(x-1)(x-3)>0 .
2. Решите неравенство :
3 .Решите неравенство графическим способом : -x2 -5x + 6 0

4 . -3х2 + 6х + 9 > 0 найдите найбольшее целое значение неравенство .
5. Ребенок имеет на руках 5 кубиков с буквами: А, К, К, Л, У. Какова вероятность того, что ребенок соберет из кубиков слово "кукла"?

Годовая контрольная работа. 7 класс
Вариант 1

1. Вычислите :
2 .Найдите значение выражения:
3.Решите уравнение :
4. Решите уравнение :
5 . Решите неравенство:
6. . Сумма квад - ра - тов цифр дву - знач - но - го числа равна 13. Если от этого числа от - нять 9, то по - лу - чит - ся число, за - пи - сан - ное теми же циф - ра - ми, но в об - рат - ном по - ряд - ке. Най - ди - те ис - ход - ное число.

Вариант 2
1. Вычислите :
2. Найдите значение выражения :
3. Решите уравнение :
4. Решите уравнение :
5. Решите неравенство :
6. По окруж - но - сти дли - ной 60 м рав - но - мер - но в одном на - прав - ле - нии дви - жут - ся две точки. Одна из них со - вер - ша - ет пол - ный обо - рот на 5 се - кунд быст - рее дру - гой. При этом сов - па - де - ние точек про - ис - хо - дит каж - дый раз через 1 ми - ну - ту. Опре - де - ли - те ско - ро - сти дви - же - ния точек.