Сүйір бұрыштың тангенсі

Сабақтың тақырыбы: §8. Тікбұрышты үшбұрыштың сүйір бұрышының синусы, косинусы, тангенсі және котангенсі.
Сабақтың мақсаты:
Білімділік: Тікбұрышты үшбұрыштың сүйір бұрышының синусын, косинусын, тангенсін, котангенсін анықтау, мәндерін табуды және берілген мәндері бойынша тік бұрышты үшбұрышты салуды үйрету.
Дамытушылық: Тікбұрышты үшбұрыштың бұрыштарын, қабырғаларын есептеуге арналған анықтамалар, формулаларды есептер шығаруда қолдана білу дағдысын қалыптастыру.
Тәрбиелік: Оқушылардың ойлау қабілетін жетілдіру, өз бетінше еңбек етуге тәрбиелеу

Сабақ түрі: Жаңа білімді меңгерту

Көрнекілігі: Сызбалар, карточкалар, слайд, интерактивті тақта, сызғыш

Сабақтың барысы:
1. Ұйымдастыру кезеңі
2. Жаңа сабақты баяндау

§8. Тікбұрышты үшбұрыштың сүйір бұрышының синусы, косинусы, тангенсі және котангенсі.
Бізге тікбұрышты үшбұрыш, оның катеттері мен гипотенузасы, сүйір бұрыштары ұғымдары белгілі. Бүгінгі сабақта тікбұрышты үшбұрыштың қабырғалары мен бұрыштарының арасындағы байланысты қарастырамыз.

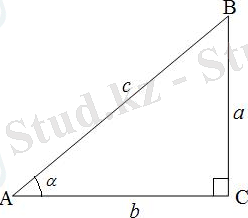
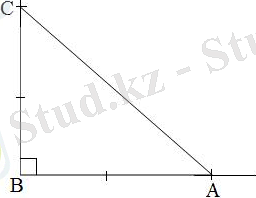
АВС тікбұрышты үшбұрыш берілген
( 27-сурет). Оның катеттері а, b ал гипотенузасы с деп, бір сүйір бұрышын мысалы А=α деп белгілейік. С=90º болсын.

27-сурет

Анықтама: Тікбұрышты үшбұрыштың сүйір бұрышына іргелес жатқан катеттің гипотенузаға қатынасы сол бұрыштың косинусы деп аталады. Оны қысқаша cosα= (1) түрінде жазады. (1) қатынас α бұрышының шамасына ғана тәуелді, қабырғалардың ұзындықтарына тәуелді емес.
20-теорема. Бұрыштың косинусы мен тек оның градустың өлшеміне ғана тәуелді.
Дәлелдеу: АВС тікбұрышты үшбұрышы берілсін. Бұл үшбұрыш үшін (1) теңдік орындалсын.

28 - сурет
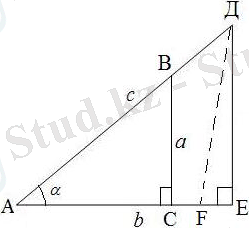
АВ сәулесіне AD=к.с кесіндісін (28-сурет). Ал АС сәулесіне АЕ=к.в (к-оң сан) өлшеп саламыз. Мұндағы, ΔADE - тікбұрышты үшбұрыш және cosα= 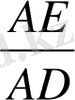екенін дәлелдейміз. Шынында 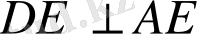болады. Керісінше ұйғарып, DE кесіндісін АЕ түзуіне перпендикуляр емес делік. Сонда D нүктесінен АЕ түзуіне DF перпендикулярын түсіруге болады. Нәтижесінде, ADF тікбұрышты үшбұрышы үшін cosα=

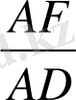
қатынасын жазамыз. Ал (1) теңдіктің негізінде 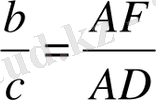аламыз, бірақ 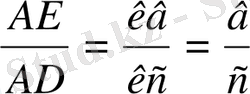немесе 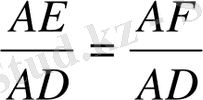болып қалады. Онда AE=AF және cosα= 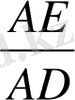шығады. Теорема дәлелденді.
Анықтама. Тікбұрышты үшбұрыштың сүйір бұрышына қарсы жатқан катеттің гипотенузаға қатынасы сол бұрыштың синусы деп аталады да,
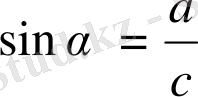(2)
түрінде жазылады.
Анықтама. Тікбұрышты үшбұрыштың сүйір бұрышына қарсы жатқан катеттің іргелес жатқан катетке қатынасы сол бұрыштың тангенсі деп аталады. Оны
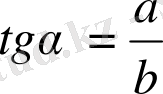(3)
түрінде жазады.

Анықтама. Тікбұрышты үшбұрыштың сүйір бұрышына іргелес жатқан катеттің қарсы жатқан катетке қатынасы сол бұрыштың катангенсі деп аталады. Оны
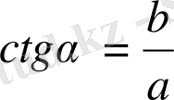(4)
түрінде жазамыз.
sinα, cosα, tgα және ctgα-ларды тригонометриялық өрнектер деп атайды.
Мысалы. Сүйір бұрышының косинусы 3:56 қатынасына тең болатын үшбұрышты салайық.
Шешуі: Ізделінді тікбұрышты үшбұрыш АВС болсын, мұндағы АВ=c-гипотенуза; <С=900; cosα= 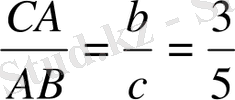теңдігі орындалу керек. Бірлік кесінді е таңдап аламыз. 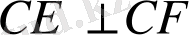сәулелерін жүргіземіз. 29 - сурет.

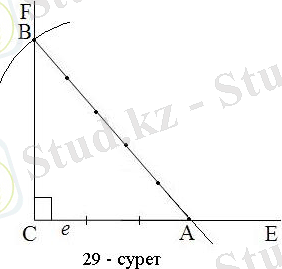
СЕ сәулесіне СА=3е кесіндісін өлшеп саламыз. Центрі А нүктесі етіп, АВ=5a кесіндісіне тең радиус етіп шеңбер жүргіземіз. Ол CF сәулесін В нүктесінде қиып өтеді. Нәтижесінде АВС тікбұрышты үшбұрышы салынады. Ол тікбұрышты үшбұрышта
cosα= 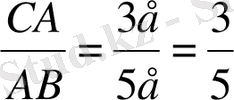болады. Демек, салынған үшбұрыш есептің шартын қанағаттандырады.

3. Есептер шығару.
№118. Сүйір бұрыштың синусы 1) 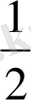; 3) 0,6-ға тең тікбұрышты үшбұрыш салыңдар.
Шешуі:

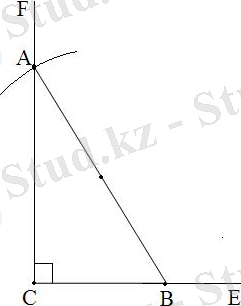
Берілгені: 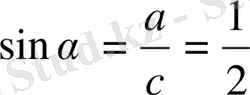СЕ сәулесіне СВ=1 бірлік кесіндіні өлшеп СВ=a=1 саламыз. Центрі В, радиусы 2-ге тең шеңбер саламыз, ол CF түзуін А нүктесінде қиып өтеді. АВС үшбұрышы есеп шартын қанағаттандырады.

3)
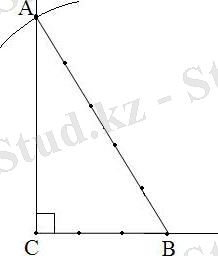sinα=0.6

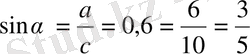
№120. Сүйір бұрыштың тангенсі 1) ; 3) 1-ге тең тікбұрышты үшбұрыш салыңдар.
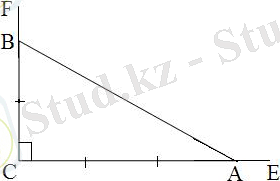1) ,
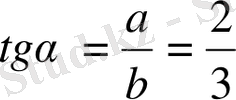
Шешуі: 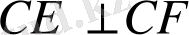түзулерін жүргізіп, СЕ сәулесінің бойына СА=3, ал CF сәулесінің бойына СВ=2 кесінділерін өлшеп саламыз. АВС - ізделінді үшбұрыш.

3) tgα=1, 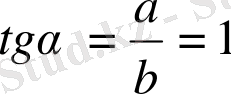да а=b екені белгілі болып отыр.

4. Қорытындылау (слайд)

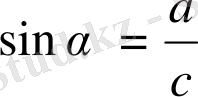cosα=

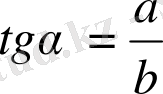
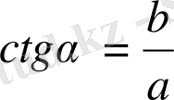
Слайд бойынша ережелерді қайталау.
5. Үйге: §8. №118(2), №119(2), №120 (2), 121 (2)