Тікбұрышты үшбұрыштардың түрлері

Скачать

Тәжірибе стансасының негізгі мектебі

Ашық сабақ тақырыбы: « Тікбұрышты үшбұрыштың сүйір бұрышының синусы, косинусы, тангенсі және сотангенсі »

VIII класс

Пән мұғалімі : Құдайберген Бисен Жетпісбай Ұлы

Қараша 2011 жылы

Сабақтың тақырыбы: Тікбұрышты үшбұрыштың сүйір бұрышының синусы, косинусы, тангенсі және сотангенесі

Сабақтың мақсаты: Білімділік. Тікбұрышты үшбұрыштың сүйір бұрышының синусы, косинусы, тангенісі және сотангенесі анықтамаларын меңгертіп, оларды үшбұрыштың элементтенрін табуға берлген есептерді шешуде қолдана білуге бейімділіктерін қалыптастыру.

Дамытушылық . Оқушылардың ой - өрісін кеңейту, матаматикалық терминдермен сөйлей отырып, сөздік қорын молайту, пәнге деген қызығушылығын арттыру.

Тәрбиелілік. Оқушыларды ұжымшылдыққа, білімділікке, білгірлікке, сауаттылыққа тәрбиеле

Көрнекілігі: 1. Тікбұрышты үшбұрыштар ( cызбалары )

2. Графопроекпор

3. Компьютер

4. Кеспе қағаздар ( карточклар )

5. Тесттер

Типі: Жаңа материалды меңгерту

Түрі: Деңгейлеп оқыту

Әдіс - тәсіл: Баяндау, сұрақ - жауап арқылы

Сабақтың жоспары: I. Өткен материалды қайталау

II. Жаңа материалды түсіндіру

III. Практикалық жұмыстар

IV. Сабақты пысықтау

V. Бағалау

VI. Үйге тапсырма

I. Үй тапсырмасы бойынша қойылатын сұрақтар:

1. Үшбұрыштың элементтерін сызбада көрсету

2. Үшбұрыштардың түрлерін ата

3. Тікбұрышты үшбұрыштардың түрлері

4. Тікбқрышты үшбұрыш туралы теорема

I I. Жаңа материалды түсіндіру:

В Берілгені: ∆ АВС

a, b - катеттері

с - гипотенузасы

c a а сүйір бұрышының косинусы деген түсінікке

назар аударайық.

Анықтама. Тікбұрышты үшбұрыштың сүйір

бұрышына іргелес жатқан гипотенузаға

қатынасы осы бұрыштың косинусы деп

А b С аталады.

Cos a - оқылуы « косинус альфа »

Қысқаша катынасты матматикалық термин түрінде жазылуы:

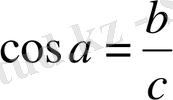
Анықтама. Тікбұрышты үшбұрыштың сүйір бұрышына қарсы жатқан катеттің гипотенузаға қатынасы сол бұрыштың синусы деп аталады

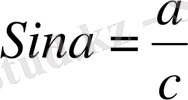
Анықтама. Тікбұрышты үшбұрыштың сүйір бұрышына іргелес жатқан катеттің іргелес жатқан катетке қатынасы сол бұрыштың тангенесі деп аталады

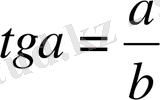
Анықтама. Тікбұрышты үшбұрыштың сүйір бұрышына іргелес жатқан катеттің қарсы жатқан катетке қатынасы сол бұрыштың котангенесі деп аталады

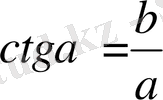
Sin a , cos a , tg a және ctg a - ларды тригонометриялық өрнектер депатайды.

Қасиеттері:

1. Қатынас а бұрышының шамасына ғана тәуелді.

2. Үшбұрыштың қабырғаларың ұзындықтарына тәуелді емес.

3. Сүйір бұрыштың косинусы, синусы, тангенсі және котангенсі бір ғана мінге ие болады.

Теорема. Бұрыштың косинусы тек оның градустық өлшеміне ғана тәуелді.

D Берілгені: ∆ АВС

а, в - катеттері

B с - гипотенузасы

c a

А E

b C F

Дәлелдеу керек: ∆ АDE

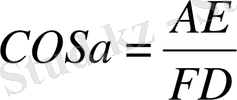
Дәлелдеу үшін: АВ сәулесіне AD = k c кесіндісін,

АС сәулесіне AE = k b ( k ˃0 ) өлшеп саламыз.

DE AE болады. Кері жорйық DE AE болмайды.

Онда D төбесінен перпендикуляр түзу жүргізуге болады, AD AE

∆ АDF тікбұрышты үшбұрыш үшін 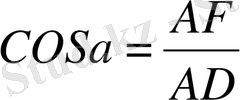деп жазамыз яғни

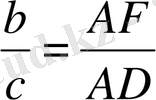теңдігін аламыз. Бірақ 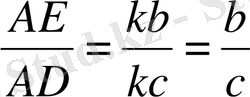немесе 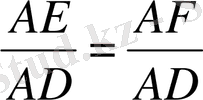осы теңдіктен

AE = AD және 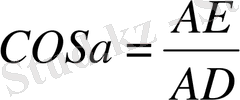теорема дәлелденді.

III. Практикалық жұмыстар:

1. Сүйір бұрыштың косинусы 3:5 қатынасына тең болатын тікбұрышты үшбұрыш салайық.

F

B , , 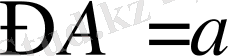ВС = a , СА = b - катеттер

C A E

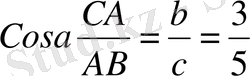e бірлік кесіндісін алайық. e CE CF cәулесін жүргіземіз

СЕ сәулесіне СА = 3 e кесіндісін өлшеп саламыз сосын А нүктесін центр етіп алып АВ = 5 е кесіндісін радиус етіп алып шеңбер жүргізсек В нүктесінде қиып өтеді. Нәтежесінде АВС тікбұрышты үшбұрыш салынады.

Осы тікбұрышты үшбұрыш 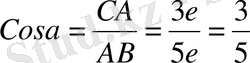болады.

Тапсырмалар: а) Cүйір бұрыштың синусы 2:5;

б) Cүйір бұрыштың сосинусы 5:8;

в) Cүйір бұрыштың синусы 1:2;

Сергіту сәті: Жазыңқы бұрыш

Параллель түзу

Тікбұрыш

Доғал бұрыш

Сүйір бұрыш

Түзу

Таблицалық тест

• Іс жүргізу
• Автоматтандыру, Техника
• Алғашқы әскери дайындық
• Астрономия
• Ауыл шаруашылығы
• Банк ісі
• Бизнесті бағалау
• Биология
• Бухгалтерлік іс
• Валеология
• Ветеринария
• География
• Геология, Геофизика, Геодезия
• Дін
• Ет, сүт, шарап өнімдері
• Жалпы тарих
• Жер кадастрі, Жылжымайтын мүлік
• Журналистика
• Информатика
• Кеден ісі
• Маркетинг
• Математика, Геометрия
• Медицина
• Мемлекеттік басқару
• Менеджмент
• Мұнай, Газ
• Мұрағат ісі
• Мәдениеттану
• ОБЖ (Основы безопасности жизнедеятельности)
• Педагогика
• Полиграфия
• Психология
• Салық
• Саясаттану
• Сақтандыру
• Сертификаттау, стандарттау
• Социология, Демография
• Спорт
• Статистика
• Тілтану, Филология
• Тарихи тұлғалар
• Тау-кен ісі
• Транспорт
• Туризм
• Физика
• Философия
• Халықаралық қатынастар
• Химия
• Экология, Қоршаған ортаны қорғау
• Экономика
• Экономикалық география
• Электротехника
• Қазақстан тарихы
• Қаржы
• Құрылыс
• Құқық, Криминалистика
• Әдебиет
• Өнер, музыка
• Өнеркәсіп, Өндіріс