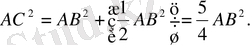Алтын қима

1.2 МЕКТЕП МАТЕМАТИКА КУРСЫНДА АЛТЫН ҚИМА ЭЛЕМЕНТТЕРІ КЕЗДЕСЕТІН БӨЛІМДЕР
Жалпы білім беретін мекемелерге арналған авторлары В.Ф.Бутузов, С.Б.Кадомцев, В.В.Прасоловтың 8-сынып геометрия оқулығында 6 тарау: үшбұрыштады шешу тарауы, 16-параграф, 71-тақырыбында алтын қима элементтері туралы алғашқы ұғым беріледі. Кітапта төмендегідей қарастырылады.
АВ кесіндісін және онда жатқан М нүктесін қарастырайық. Егер (96-сурет) болған жағдайда АМ және МВ кесінділері алтын қима құрайды делінеді, яғни кесіндінің үлкен бөлігінің жалпы кесіндіге қатынасы, кіші бөліктің үлкен бөлікке қатынасына тең.

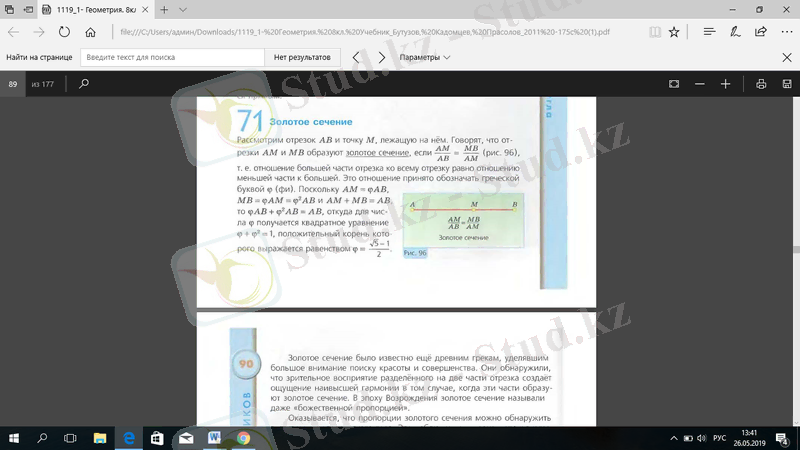
96-сурет. Алтын қима
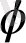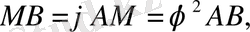
Бұл қатынаc гректің (фи) әріпімен белгіленеді. 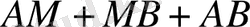болса, онда 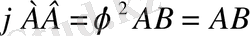, үшін квадраттық теңдеу 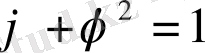орындалып, оның он түбірі 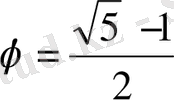тең болады.
Алтын қима сұлулық пен кемелдікке көп көңіл бөлген ежелгі гректерге де белгілі болатын. Олар бұл бөліктер алтын қима құраған жағдайда екі бөлікке бөлінген бөлікті көру ең жоғары үйлесім сезімін тудырадындығын дәлелдеді. Қайта өрлеу дәуірінде алтын қима тіпті <<құдайдың пропорциясы>> деп аталды.
Тіптен алтын қима пропорцияларын адам денесінің құрылымынан да кездестіруге болады. Бұл бақылау түрі мүсіншілерде кеңінен қолданылады. Мысалға, атақты Аполлон Бельведерскийдің мүсінінде алтын қима элементтері көптеп кездеседі. Тіптен АМ:МВ қатынасын білдіретін 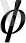әріпі де кездейсоқ бұлай аталмаған - бұл өзінің туындыларында алтын қиманы жүйелі түрде пайдаланған атақты ежелгі грек мүсіншісі Фидияның есімінің бірінші әріпі.
Алтын қима архитектурада да жиі кездеседі. Нерлидегі Богородица жамылғысы шіркеуі мысал бола алады, оның әртүрлі конструкциялары арасындағы ара қашықтықтың жұптық қатынасы 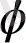-ге тең. Басқа мысал - Римдегі Palazzo Conctllaria ішкі алаңы тікбұрышты пішінге ие және аралас тараптардың қатынасы 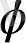- ге тең. Алтын қима Сальвадор Далидің, Казимир Малевичтің және тағы да басқа суретшілердің бірқатар композицияларының негізіне жатады.

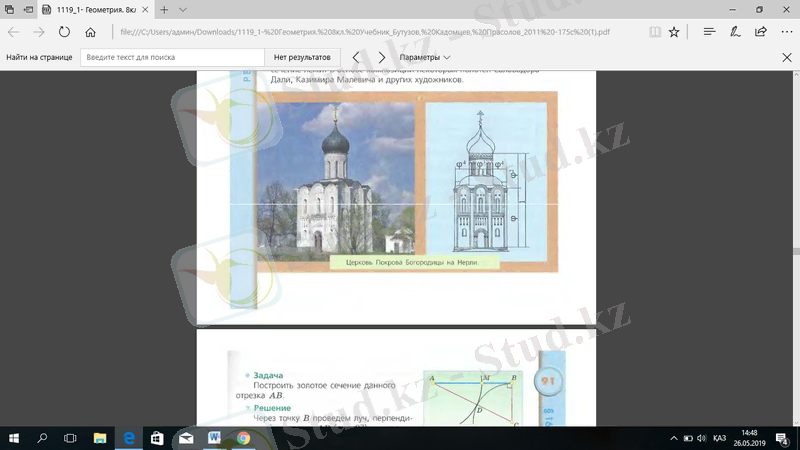
Нерлидегі Богородица жамылғысы шіркеуі

Есеп. Берілген АВ кесіндісінде алтын қима тұрғызу.
Шешуі. В нүктесі арқылы АВ кесіндісіне (97-сурет) перпендикуляр сәуле жүргіземіз және одан АВ-ның жартысына тең ВС кесіндісін аламыз. Содан кейін С центрі болатын ВС радиусымен шеңбер жүргіземіз және оның АС кесіндісімен қиылысу нүктесін D деп белгілейміз. М ізделінді нүктесі центрі А, АD радиусы болатын және АВ кесіндісінде шеңбердің қиылысу нүктесі болып табылады.
Негізінде, Пифогор теоремасы бойынша

Осы жерден 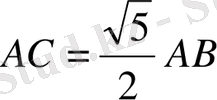, сондықтан

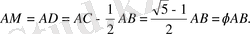
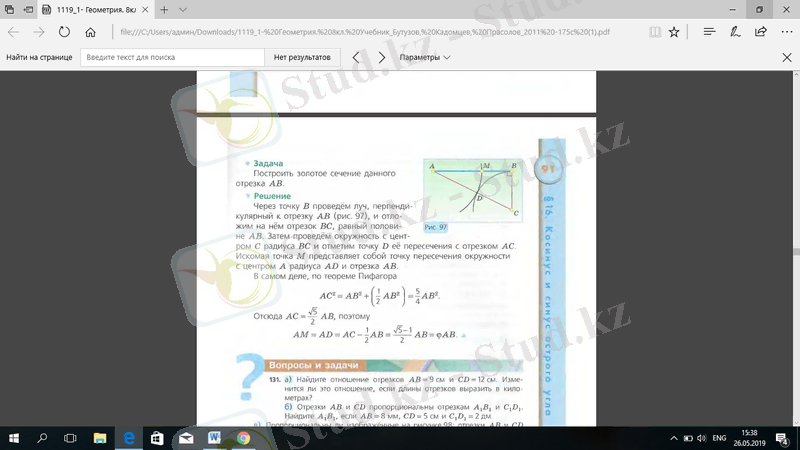
97-сурет. АВ кесіндісінде алтын қима тұрғызу
Сұрақтар және тапсырмалар:
131. а) АВ = 9 см және СD = 12 см кесінділердің қатынасын табыңыз. Егер кесінділердің ұзындығын километр арқылы белгілесек бұл қатынас өзгереді ме?
б) АВ және СD кесінділері 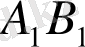және кесінділеріне пропорционал. Егер 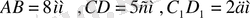болса, 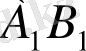-ді табыңыз.
в) 98-суреттегі бейнелеулер пропорционалды бола ма: АВ және CD кесінділері FH және GH кесінділеріне; АВ, ВС және CD кесінділері FH, EF және EG кесінділеріне?
г) ABCD параллелограмының диагоналдары О нүктесінде қиылысады, АВ және АО кесінділері AD және АС кесінділеріне пропорционал. Егер ВС = 8 см болса, CD табыңыз.
д) С және 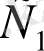нүктелері кесінділерінде жатады, АС және ВС кесінділері 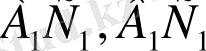кесінділеріне пропорционал. 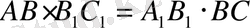екенін дәлелдеңіз.
е) MN кесіндісін сызыңыз және К нүктесін салыңыз, MK:KN = 4:3 болатындай.

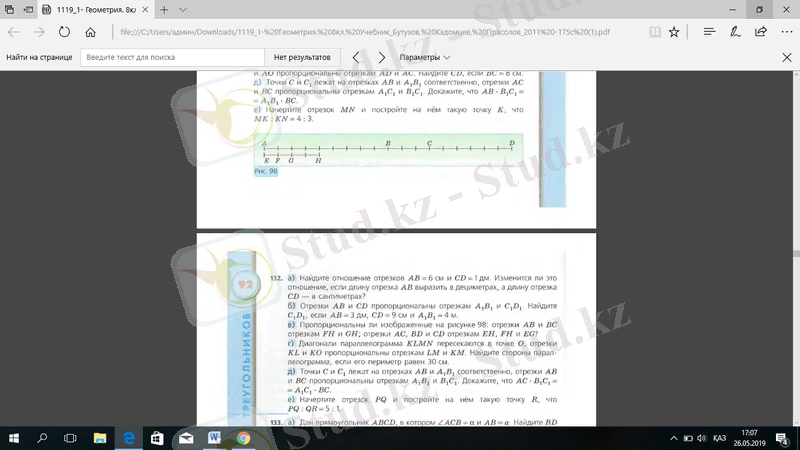
98-сурет
132. а) AB = 6 см және CD = 1 дм кесінділерінің қатынасын табыңыз. Бұл қатынас AB кесіндісін ұзындығын дициметрмен, CD кесіндісінің ұзындығын сантиметрмен белгілесек өзгереді ме?
б) AB және CD кесінділері 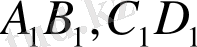кесінділеріне пропорционал болады ма, егер AB = 3 дм, CD = 9 см және 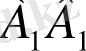= 4 м болса.
в) 98-суреттегі бейнелеулер пропорционалды бола ма: АВ және ВС кесінділері FH және GH кесінділеріне; АВ, ВD және CD кесінділері EH, FH және EG кесінділеріне?
г) KLMN параллелограмының диагоналдары О нүктесінде қиылысады, KL және KО кесінділері LM және KM кесінділеріне пропорционал. Егер оның периметрі 30 см болса, параллелограмның қабырғаларын табыңыз.
д) С және 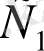нүктелері кесінділерінде жатады, АВ және ВС кесінділері 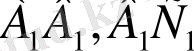кесінділеріне пропорционал. 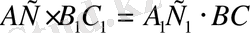екенін дәлелдеңіз.
е) PQ кесіндісін сызыңыз және R нүктесін салыңыз, PQ:QR = 5:1 болатындай.
133. а) 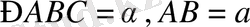болатын ABCD тікбұрышы берілген. BD және AD табыңыз.
б) Бұрыштары 30 және 60 болатын синус пен косинустың мағынасын табыңыз.
в) Егер 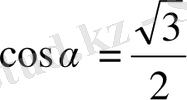болса, 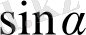неге тең?
г) Косинус 0.3 тең бұрыш тұрғызыңыз.
д) АВ кесіндісі берілген. АВ және 2АВ кесінділерінің орташа геометриялық кесіндін тұрғызыңыз және оның ұзындығын табыңыз.
е) СН кесіндісі - АВС тікбұрышты үшбұрышының биіктігі. АВ гипотенузасының және АН кесіндісінің орташа геометриялық катеті АС болатынын дәлелдеңіз.
ж) СD кесіндісі - АВС үшбұрышының биіктігі, 90 , AD = 9 см, DB = 16 см болса. sinA және cosA табыңыз.
з) АВС тікбұрышты үшбұрышының АВ гипотенузасына Е нүктесі белгіленген, ал АС катетінде - С нүктесі, сондықтан . Егер AE = 15 мм, BE = 20 мм, DE = DC болса, ABC үшбұрышының периметрін табыңыз.
и) СD кесіндісі - С бұрышы тік болған АВС үшбұрышының биіктігі. 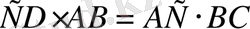екенін дәләлдеңіз.
134. а) 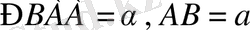болатын ABCD тікбұрышы берілген. BD және AD табыңыз.
б) және 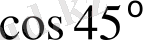табыңыз.
в) Егер 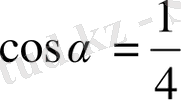, табыңыз.
г) Синусы 0,3 тең сүйір бұрыш салыңыз.
д) АВ кесіндісі берілген. - ға тең кесінді тұрғызыңыз.
е) А нүктесі арқылы центрі О нүктесі болатын шеңберге жанама жүргізілген, жанасу нүктесінен АО түзуіне ВН перпендикуляры жүргізілген. Шеңбердің радиусы ОА және ОН кесінділеріне орташа геометриялық болатынын дәлелдеңіз.
ж) ABCD трапециясының А бұрышын табыңыз. Егер BC = 2, AD = 4 және .
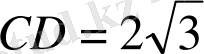з) АВС тікбұрышты үшбұрышының АВ гипотенузасына D нүктесі белгіленген, ал АС катетінде - E нүктесі, сондықтан . Егер ВD = DE, AE = 5 дм, EС = 4 дм болса, BC табыңыз.
и) ВМ және АН кесінділері - негізі АС болатын теңбүйірлі АВС үшбұрышының медиана және биіктігі. 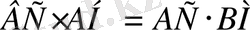екенін дәлелдеңіз.
135. а) СН кесіндісі - АВС үшбұрышының биіктігі, 90 , AС = 6 см және BС = 8 см. АВ, АН және НВ табыңыз.
б) Тікбұрышты трапецияның негіздері 8 см және 12 см тең, үлкен диагоналы 13 см тең. Трапецияның шеткі қабырғаларын табыңыз.
в) АВ = 9 см, ВD = 12 см және AD = 15 см ABCD трапеция берілген. CBD бұрышының синус және косинусын табыңыз.
г) Теңбүйірлі трапецияның өзара перпендикуляр диагоналдарының тұйық бұрышының төбесі арқылы түзу жүргізілген, негіздеріне перпендикуляр және олардың үлкенін екі кесіндіге бөлетін, олардың ең кішісі 10 см-ге тең. Егер трапецияның бүйір қабырғасы 26 см болса, оның негізін табыңыз.
д) ВН кесіндісі - АВС сүйір үшбұрышының биіктігі. екенін дәлелдеңіз.
е) Жақтары болатын үшбұрыштың жақтарын табыңыз.
ж) Үшбұрыштың a және b жақтары алтын қима құрайды, яғни . Егер осы үшбұрыштан жағы b болатын квадрат кесіліп алынсын, сонда үшбұрыштың қалған аралас жақтары алтын қима құрайтындығын дәлелдеңіз.
136. а) СН кесіндісі - С бұрышы тік болған АВС үшбұрышының биіктігі. Егер AВ = 20 см және AС = 16 см, ВС, АН және СН табыңыз.
б) Тікбұрышты трапецияның негіздері 9 см және 18 см тең, үлкен диагоналы 15 см тең. Трапецияның диагоналын табыңыз.
в) Тікбұрышты трапецияға жазылған шеңбердің радиусын табыңыз, егер трапецияның негіздері 3 және 6 тең болса.
г) Егер ABCD төртбұрышының диагоналдары өзара перпендикуляр болса, онда дәлелдеңіз.
д) ВН кесіндісі - А бұрышы тұйық болған АВС үшбұрышының биіктігі. дәлелдеңіз.
е) Жақтары болатын үшбұрыштың жақтарын табыңыз.
ж) Үшбұрыштың a және b жақтары алтын қима құрайды, яғни . Егер осы үшбұрышқа тікбұрыш пайда болатындай жағы а болатын квадрат салынсын, сонда үшбұрыштың қалған аралас жақтары алтын қима құрайтындығын дәлелдеңіз.