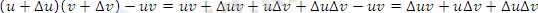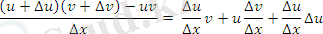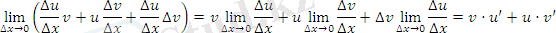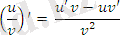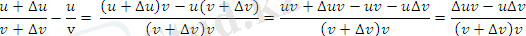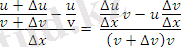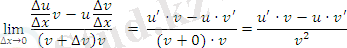Туындыны табу ережелері: теория және практикалық есептер
Сабақтың тақырыбы: Туындыны табу ережелері
Сабақ мақсаты:
Туындыны табу ережелері бойынша формуласымен танысып, оларды еесеп шығаруда қолдануды үйрету.
Туындының ұғымы бойынша білімдерін дамыту
Оқуға саналы сезімге жауапкершілікке өз бетінше еңбектенуге тәрбиелеу.
Сабақтың түрі:
Әдісі:
Көрнекілігі:
Сабақ барысы:
Ұйымдыстыру кезеңі
Жаңа сабақ
Есептер шығару
Үйге тапсырма
Қорытынды
Жоспар:
1. Туынды ережелерінен түсінік беру.
2. Ауызша тапсырма, салыстырмалы түрде.
3. Кітаппен жұмыс.
4. Тест( тестрмен) интерактифті тақта бойын
1-ереже
Егер и және υ функцияларының х нүктесінде и', υ' туындылары бар болса, онда и+υ функциясының х нүктесіндегі туындысы бар және ол
(и+υ) ' = и' + υ' формуласымен анықталады
Мысалы:
f(x) = x² - x + 5
Шешуі:
f ' (x) = (x² - x + 5) = (x²) ' - (x) ' + (5) ' = 2x - 1 + 0 = = 2x - 1
2 - ереже
Егер u және v функцияларының х нүктесінде туындылары бар болса, онда берілген функциялардың көбеитіндісі u v функциясының осы х нүктесінде туындысы бар және ол
( uv) ' = u'v+ uv'
формуласымен анықталады.
Дәлелдеу
Туындының алгоритмін қолданамыз; х-∆х өсімшесіне сәикес келетін uv функциясының өсімшесінің өрнегін анықтайық.
Аргумент өсімшесіне бөлеміз:
∆х→0
Салдар
С тұрақты сан болса, онда Cf (x) функциясының туындысы бар және ол
(Cf (x) ) '=Cf '(x)
формуламен анықталады, тұрақты көбейткішті туынды белгісіның алдына шығаруға болады.
Мысал: y=(3x²-7x+5) (2x-3)
Шешуі: u=3x²-7x+5, v=2x-3 u'=6x-7, v'=2
(uv) ' = u'v+ uv'
y'=((3x²-7x+5) (2x-3) ) '=(6x-7) (2x-3) +2·(3x²-7x+5) =12x²-14x-18x+21+6x²-14x+10=18x²-46x+31
3 - ереже
Егер u және v функцияларының х нүктесінде туындылары бар және v ≠0 болса онда функциясының да х нүктесінде туындысы бар және ол туынды
формуласы арқылы анықталады.
Дәлелдеу
Алгоритмін қолданамыз, аргументтің u функциясының өсімшесін v функциясының өсімшесін деп алып функциясының өсімшесін анықтайық.
Аргумент өсімшесі ∆х-ке бөлеміз:
∆х→0 жағдайда шегін анықтаймыз.
Мысал:
y=x
n
дәрежелі функцияның туындысы.
(x
n
) ' = nx
n-1
(x
-m
) ' = -m·x
-m -1
№178
f(х) =×(×+1), ×0f(х) = \times ( \times + 1), \times_{0}f(х) =×(×+1), ×0f(х) = \times ( \times + 1), \times_{0}=2
f
´
(
х
)
=
×
•
(
×
+
1
)
)
=
×
´
•
(
×
+
1
)
+
×
(
×
+
1
)
´
=
(
×
+
1
)
+
×
=
×
+
1
+
×
=
2
×
+
1
f´(х) = \times \bullet ( \times + 1) ) = \times ´ \bullet ( \times + 1) + \times ( \times + 1) ´ = ( \times + 1) + \times = \times \ \ \ \ \ \ \ \ \ \ + 1 + \times = 2 \times + 1
f
´
(
х
)
=
×
•
(
×
+
1
)
)
=
×
´
•
(
×
+
1
)
+
×
(
×
+
1
)
´
=
(
×
+
1
)
+
×
=
×
+
1
+
×
=
2
×
+
1
f´(х) = \times \bullet ( \times + 1) ) = \times ´ \bullet ( \times + 1) + \times ( \times + 1) ´ = ( \times + 1) + \times = \times \ \ \ \ \ \ \ \ \ \ + 1 + \times = 2 \times + 1
f
(
х
)
=
2
•
2
+
1
=
5
\ \ \ \ \ f(х) = 2 \bullet 2 + 1 = 5
f
(
х
)
=
2
•
2
+
1
=
5
\ \ \ \ \ f(х) = 2 \bullet 2 + 1 = 5
;
f(х) =×2•(×−5) ×2=−2f(х) = \times^{2} \bullet ( \times - 5) \ \ \times_{2} = - 2f(х) =×2•(×−5) ×2=−2f(х) = \times^{2} \bullet ( \times - 5) \ \ \times_{2} = - 2
f´
=
(
×
2
•
(
×
−
5
)
)
´
=
(
×
2
)
´
•
(
×
−
5
)
+
×
2
(
×
−
5
)
´
=
2
×
(
×
−
5
)
+
×
2
•
1
=
2
×
2
−
10
×
+
×
2
=
3
×
2
−
10
×
= \left( \times_{2} \bullet ( \times - 5) \right) ´ = \left( \times^{2} \right) ´ \bullet ( \times - 5) + \times^{2}( \times - 5) ´ = 2 \times ( \times - 5) + \times^{2} \bullet 1 = 2 \times^{2} - 10 \times + \times^{2} = 3 \times^{2} - 10 \times
=
(
×
2
•
(
×
−
5
)
)
´
=
(
×
2
)
´
•
(
×
−
5
)
+
×
2
(
×
−
5
)
´
=
2
×
(
×
−
5
)
+
×
2
•
1
=
2
×
2
−
10
×
+
×
2
=
3
×
2
−
10
×
= \left( \times_{2} \bullet ( \times - 5) \right) ´ = \left( \times^{2} \right) ´ \bullet ( \times - 5) + \times^{2}( \times - 5) ´ = 2 \times ( \times - 5) + \times^{2} \bullet 1 = 2 \times^{2} - 10 \times + \times^{2} = 3 \times^{2} - 10 \times
f
(
−
2
)
=
3
•
(
−
2
)
2
−
10
•
(
−
2
)
=
3
•
4
+
20
=
32
f( - 2) = 3 \bullet ({- 2) }^{2} - 10 \bullet ( - 2) = 3 \bullet 4 + 20 = 32
f
(
−
2
)
=
3
•
(
−
2
)
2
−
10
•
(
−
2
)
=
3
•
4
+
20
=
32
f( - 2) = 3 \bullet ({- 2) }^{2} - 10 \bullet ( - 2) = 3 \bullet 4 + 20 = 32
;
f(х) =(×−2) (×+3), ×0=−1f(х) = ( \times - 2) ( \times + 3), \times_{0} = - 1f(х) =(×−2) (×+3), ×0=−1f(х) = ( \times - 2) ( \times + 3), \times_{0} = - 1
f
´
=
(
(
×
−
2
)
(
×
+
3
)
)
´
=
(
×
−
2
)
´
(
×
+
3
)
+
(
×
−
2
)
(
×
+
3
)
´
=
1
(
×
+
3
)
(
×
−
2
)
•
1
=
×
+
3
+
×
−
2
=
2
×
+
1
f´ = \left( ( \times - 2) ( \times + 3) \right) ´ = ( \times - 2) ´( \times + 3) + ( \times - 2) ( \times + 3) ´ = 1( \times + 3) ( \times - 2) \bullet 1 = \times + 3 + \times - 2 = 2 \times + 1
f
(
−
1
)
=
2
•
(
−
1
)
+
1
=
−
2
+
1
=
−
1
f( - 1) = 2 \bullet ( - 1) + 1 = - 2 + 1 = - 1
f
(
−
1
)
=
2
•
(
−
1
)
+
1
=
−
2
+
1
=
−
1
f( - 1) = 2 \bullet ( - 1) + 1 = - 2 + 1 = - 1
;
f(×) =×+1×−2( \times ) = \frac{\times + 1}{\times - 2\ }(×) =×+1×−2( \times ) = \frac{\times + 1}{\times - 2\ }×0\times_{0}×0\times_{0}=1
f´
(
×
)
=
(
×
+
1
´
)
•
(
×
−
2
)
−
(
×
+
1
)
•
(
×
−
2
)
´
)
(
×
−
2
)
2
=
1
(
×
−
2
)
−
(
×
+
1
)
•
1
(
×
−
2
)
2
=
×
−
2
−
×
−
1
(
×
−
2
)
2
=
−
3
(
×
−
2
)
2
( \times ) = \frac{\left( \times + 1´) \bullet ( \times - 2) - ( \times + 1) \bullet ( \times - 2) ´ \right) }{( \times - {2) }^{2}} = \frac{1( \times - 2) - ( \times + 1) \bullet 1}{( \times - {2) }^{2}} = \frac{\times - 2 - \times - 1}{( \times - {2) }^{2}} = \frac{- 3}{( \times - {2) }^{2}}
(
×
)
=
(
×
+
1
´
)
•
(
×
−
2
)
−
(
×
+
1
)
•
(
×
−
2
)
´
)
(
×
−
2
)
2
=
1
(
×
−
2
)
−
(
×
+
1
)
•
1
(
×
−
2
)
2
=
×
−
2
−
×
−
1
(
×
−
2
)
2
=
−
3
(
×
−
2
)
2
( \times ) = \frac{\left( \times + 1´) \bullet ( \times - 2) - ( \times + 1) \bullet ( \times - 2) ´ \right) }{( \times - {2) }^{2}} = \frac{1( \times - 2) - ( \times + 1) \bullet 1}{( \times - {2) }^{2}} = \frac{\times - 2 - \times - 1}{( \times - {2) }^{2}} = \frac{- 3}{( \times - {2) }^{2}}
;
f´(×) =0f´( \times ) = 0f´(×) =0f´( \times ) = 0
f
(
×
)
=
×
3
−
3
×
2
f( \times ) = \times^{3} - {3 \times}^{2}
f
(
×
)
=
×
3
−
3
×
2
f( \times ) = \times^{3} - {3 \times}^{2}
+7
f
´
(
×
)
=
(
×
3
−
3
×
2
+
7
)
´
=
3
×
2
−
6
×
f´( \times ) = \left( \times^{3} - {3 \times}^{2} + 7 \right) ´ = {3 \times}^{2} - 6 \times
3
×
2
−
6
×
=
0
{3 \times}^{2} - 6 \times = 0
3
×
(
×
−
2
)
=
0
3 \times ( \times - 2) = 0
3
×
=
0
3 \times = 0
×
=
0
\times = 0
×
−
2
=
0
\times - 2 = 0
×
=
2
\times = 2
(
0
,
2
)
(0, 2)
f(×) =3×3−2×3f( \times ) = {3 \times}^{3} - {2 \times}^{3}f(×) =3×3−2×3f( \times ) = {3 \times}^{3} - {2 \times}^{3}-1
f
´
(
×
)
=
(
3
×
3
−
2
×
3
−
1
)
=
9
×
2
−
6
×
2
f´( \times ) = \left( {3 \times}^{3} - {2 \times}^{3} - 1 \right) = {9 \times}^{2} - {6 \times}^{2}
9
×
2
−
6
×
=
0
{9 \times}^{2} - 6 \times = 0
3
×
(
3
×
−
2
)
=
0
\times (3 \times - 2) = 0
×
(
3
×
−
2
)
=
0
\times (3 \times - 2) = 0
3
×
=
0
\times = 0
×
=
0
\times = 0
×
=
0
\times = 0
3
×
−
2
=
0
\times - 2 = 0
×
−
2
=
0
\times - 2 = 0
3
×
=
2
3
\times = \frac{2}{3}
×
=
2
3
\times = \frac{2}{3}
№184
f
´
(
×
)
>
0
f´( \times ) > 0
а)
f
(
×
)
=
1
3
×
3
+
4
×
2
−
9
×
+
1
f( \times ) = \frac{1}{3} \times^{3} + {4 \times}^{2} - 9 \times + 1
f
(
×
)
=
1
3
×
3
+
4
×
2
−
9
×
+
1
f( \times ) = \frac{1}{3} \times^{3} + {4 \times}^{2} - 9 \times + 1
f
´
(
×
)
=
×
2
+
8
×
−
9
f´( \times ) = \times^{2} + 8 \times - 9
D>0 а>0
×
2
+
8
×
−
9
>
0
\times^{2} + 8 \times - 9 > 0
D
=
64
+
4
•
9
=
100
= 64 + 4 \bullet 9 = 100
=
64
+
4
•
9
=
100
= 64 + 4 \bullet 9 = 100
×
1
=
−
8
−
10
8
>
1
\times_{1} = \frac{- 8 - 10}{8} > 1
×
2
=
−
8
−
10
8
<
−
9
\times_{2} = \frac{- 8 - 10}{8} < - 9
(
−
∞
−
9
)
⋃
(
1
+
∞
)
( - \infty - 9) \bigcup(1 + \infty)
б)
f
(
×
)
=
1
3
×
3
+
×
2
+
3
×
\ f( \times ) = \frac{1}{3} \times^{3} + \times^{2} + 3 \times
f
(
×
)
=
1
3
×
3
+
×
2
+
3
×
\ f( \times ) = \frac{1}{3} \times^{3} + \times^{2} + 3 \times
f
´
(
×
)
=
−
×
2
+
2
×
+
3
f´( \times ) = {- \times}^{2} + 2 \times + 3
−
×
2
+
2
×
+
3
{- \times}^{2} + 2 \times + 3
D
=
4
+
4
•
3
=
16
= 4 + 4 \bullet 3 = 16
=
4
+
4
•
3
=
16
= 4 + 4 \bullet 3 = 16
×
1
=
−
2
+
4
−
2
=
2
−
2
=
−
1
\times_{1} = \frac{- 2 + 4}{- 2} = \frac{2}{- 2} = - 1
×
2
=
−
2
−
4
−
2
=
−
6
−
2
=
3
\times_{2} = \frac{- 2 - 4}{- 2} = \frac{- 6}{- 2} = 3
№185
f
´
(
×
)
≤
0
\ f´( \times ) \leq 0
а)
f
(
×
)
=
2
×
4
−
×
\ f( \times ) = {2 \times}^{4} - \times
f
(
×
)
=
2
×
4
−
×
\ f( \times ) = {2 \times}^{4} - \times
f
´
(
×
)
=
8
×
3
−
1
f´( \times ) = {8 \times}^{3} - 1
f
´
(
×
)
=
8
×
3
−
1
f´( \times ) = {8 \times}^{3} - 1
8
×
3
−
1
≤
0
{8 \times}^{3} - 1 \leq 0
8
×
3
−
1
≤
0
{8 \times}^{3} - 1 \leq 0
8
×
3
≤
1
{8 \times}^{3} \leq 1
8
×
3
≤
1
{8 \times}^{3} \leq 1
×
≤
1
2
\times \leq \frac{1}{2}
×
≤
1
2
\times \leq \frac{1}{2}
×
3
≤
1
8
\times^{3} \leq \frac{1}{8}
×
3
≤
1
8
\times^{3} \leq \frac{1}{8}
(
−
∞
;
1
2
]
\left( - \infty; \right. \ \left. \ \frac{1}{2} \right\rbrack
(
−
∞
;
1
2
]
\left( - \infty; \right. \ \left. \ \frac{1}{2} \right\rbrack
ә)
f
(
×
)
=
1
×
−
2
×
−
1
\ f( \times ) = \frac{1}{\times}{- 2 \times - 1}^{}
f
(
×
)
=
1
×
−
2
×
−
1
\ f( \times ) = \frac{1}{\times}{- 2 \times - 1}^{}
f
´
(
×
)
=
(
1
×
)
´
−
(
2
×
)
=
×
−
1
−
1
−
2
=
−
×
−
2
−
2
f´( \times ) = \left( \frac{1}{\times} \right) ´ - (2 \times ) = \times^{- 1 - 1} - 2 = - \times^{- 2} - 2
f
´
(
×
)
=
(
1
×
)
´
−
(
2
×
)
=
×
−
1
−
1
−
2
=
−
×
−
2
−
2
f´( \times ) = \left( \frac{1}{\times} \right) ´ - (2 \times ) = \times^{- 1 - 1} - 2 = - \times^{- 2} - 2
−
1
×
2
−
2
≤
0
\frac{- 1}{\times^{2}} - 2 \leq 0
−
1
×
2
−
2
≤
0
\frac{- 1}{\times^{2}} - 2 \leq 0
−
1
×
2
−
2
≤
2
\frac{- 1}{\times^{2}} - 2 \leq 2
−
1
×
2
−
2
≤
2
\frac{- 1}{\times^{2}} - 2 \leq 2
-1
≤
2
×
2
\leq {2 \times}^{2}
≤
2
×
2
\leq {2 \times}^{2}
×
2
≥
1
2
\times^{2} \geq \frac{1}{2\ }
×
2
≥
1
2
\times^{2} \geq \frac{1}{2\ }
×
>
1
2
\times > \sqrt{\frac{1}{2}}
×
>
1
2
\times > \sqrt{\frac{1}{2}}
;
б)
f
(
×
)
=
×
3
−
27
×
\ f( \times ) = \times^{3} - 27 \times
f
(
×
)
=
×
3
−
27
×
\ f( \times ) = \times^{3} - 27 \times
f
´
(
×
)
=
3
×
2
−
27
×
\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ f´( \times ) = {3 \times}^{2} - 27 \times
f
´
(
×
)
=
3
×
2
−
27
×
\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ f´( \times ) = {3 \times}^{2} - 27 \times
3
×
2
−
27
≤
0
{3 \times}^{2} - 27 \leq 0
3
×
2
−
27
≤
0
{3 \times}^{2} - 27 \leq 0
3
×
2
≤
27
{3 \times}^{2} \leq 27
3
×
2
≤
27
{3 \times}^{2} \leq 27
×
2
≤
9
{\ \ \times}_{2} \leq 9
×
2
≤
9
{\ \ \times}_{2} \leq 9
×
\ \times
×
\ \times
(
−
3
;
3
)
\ \ \ \ \ \ \ \ ( - 3; 3)
№186
f
(
×
)
=
(
4
×
+
3
)
(
4
×
−
3
)
+
2
×
2
=
4
×
−
3
2
+
2
×
2
=
16
×
4
−
9
+
2
×
2
f( \times ) = \left( 4\sqrt{\times + 3} \right) \left( 4\sqrt{\times - 3} \right) + 2 \times^{2} = 4\sqrt{\times} - 3^{2} + 2 \times^{2} = 16 \times^{4} - 9 + 2 \times^{2}
f
´
(
×
)
=
(
16
×
−
9
+
2
×
2
)
´
=
16
+
4
×
;
f´( \times ) = \left( 16 \times - 9 + 2 \times^{2} \right) ´ = 16 + 4 \times ;
f
(
×
)
=
(
×
2
+
5
)
(
×
2
−
4
)
+
2
×
=
×
4
+
5
×
2
−
4
×
2
−
20
=
×
4
+
×
2
−
20
f( \times ) = \left( \times^{2} + 5 \right) \left( \times^{2} - 4 \right) + 2\sqrt{\times} = \times^{4} + 5 \times^{2} - 4 \times^{2} - 20 = \times^{4} + \times^{2} - 20
f
´
(
×
)
=
(
×
4
−
×
2
−
20
)
=
4
×
3
−
2
×
;
f´( \times ) = \left( \times^{4} - \times^{2} - 20 \right) = {4 \times}^{3} - 2 \times ;
№189
а)
f
(
×
)
=
×
2
+
2
×
+
3
×
2
+
2
×
+
5
f( \times ) = \frac{\times^{2} + 2 \times + 3}{\times^{2} + 2 \times + 5}
(
×
2
+
2
×
+
3
)
´
=
2
×
+
2
\left( \times^{2} + 2 \times + 3 \right) ´ = 2 \times + 2
(
×
2
+
2
×
+
5
)
\left( \times^{2} + 2 \times + 5 \right)
(
×
2
+
2
×
+
5
)
\left( \times^{2} + 2 \times + 5 \right)
´
=
2
×
+
2
= 2 \times + 2
=
2
×
+
2
= 2 \times + 2
f
´
(
×
)
=
(
×
2
+
2
×
+
3
×
2
+
2
×
+
5
)
´
=
(
2
×
+
2
)
•
(
×
2
+
2
×
+
5
)
−
(
×
2
+
2
×
+
3
)
•
(
2
×
+
2
)
(
×
2
+
2
×
+
5
)
2
=
2
×
3
+
4
×
2
+
10
×
+
2
×
2
+
4
×
2
+
10
−
2
×
3
−
4
×
2
−
6
×
−
2
×
3
−
4
×
2
−
6
(
×
2
+
2
×
+
5
)
2
=
4
×
+
4
(
×
2
+
2
×
+
5
)
2
;
f´( \times ) = \left( \frac{\times^{2} + 2 \times + 3}{\times^{2} + 2 \times + 5} \right) ´ = \frac{(2 \times + 2) \bullet \left( \times^{2} + 2 \times + 5 \right) - \left( \times^{2} + 2 \times + 3 \right) \bullet (2 \times + 2) }{{( \times}^{2} + 2 \times + {5) }^{2}} = \frac{2 \times^{3} + {4 \times}^{2\ } + 10 \times + 2 \times^{2} + {4 \times}^{2\ } + 10 - 2 \times^{3} - {4 \times}^{2\ } - 6 \times - 2 \times^{3} - {4 \times}^{2\ } - 6}{{( \times}^{2} + 2 \times + {5) }^{2}} = \frac{4 \times + 4}{{( \times}^{2} + 2 \times + {5) }^{2}};
4
×
+
4
×
2
+
2
×
+
5
=
0
\frac{4 \times + 4}{\times^{2} + 2 \times + 5} = 0
4
×
+
4
=
0
4 \times + 4 = 0
4
×
=
−
4
4 \times = - 4
×
=
−
1
\times = - 1
б)
f
(
×
)
=
1
−
3
×
+
×
2
1
+
×
+
×
2
f( \times ) = \frac{1 - 3 \times + \times^{2}}{1 + \times + \times^{2}}
(
1
−
3
×
+
×
2
)
´
=
−
3
+
2
×
\left( 1 - 3 \times + \times^{2} \right) ´ = - 3 + 2 \times
(
1
+
×
+
×
2
)
´
=
1
+
2
×
\left( 1 + \times + \times^{2} \right) ´ = 1 + 2 \times
Ұқсас жұмыстар