Дифференциалдық теңдеулер

Ф-Е-10/3

Сабаққа жіберілді: _______________________

_______________________

_______________________
№___ сабақ жоспары
Мамандығы: 1304000 «Есептеу механикасын бағдарламамен
қамтамасыздандыру»
Пәні: Жоғары математика негіздері

|Тобы |ТБ-13/11 |ТБ-12/9 |
|Күні |06.09.2014|06.09.2014|

Сабақтың тақырыбы: Дифференциалдық теңдеулер туралы ұғым

Сабақтың мақсаты: Білімділік: Оқушыларға дифференциалдық теңдеулер,
оның негізгі
қасиеттерін,
түсіндіру, математикалық
тапсырмалардың
орындалу жолдарын үйрету.

Дамытушылық: Оқушыларға практикалық тапсырмалар, өз бетінше
орындалатын
тапсырмаларды
орындата отырып, олардың есептерді шығаруға
дағдыландыру.
Тәрбиелік: Оқушыларға әртиптегі
тапсырмалар орындата отырып, пәнге деген
қызығушылығын
арттыру

Сабақтың типі: жаңа материалды оқыту сабағы

Сабақтың түрі: Кіріспе

Сабақтың барысы мен мазмұны:
I. Ұйымдастыру кезеңі
Сәлемдесу, оқушыларды түгелдеу, аудитория тазалығын тексеру
II. Сабақтың мақсаты мен жоспарын хабарлау
Дифференциалдық теңдеулер туралы ұғым.

IІІ. Жаңа материалды түсіндіру

Дифференциалдық теңдеулер.[:]
[gl]§1. Дифференциалдық теңдеулер жөніндегі негізгі түсінік.[:]
Тәуелсіз х, ізделінетін функция 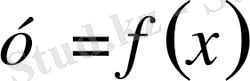және оның туындыларын
байланыстыратын байланыстыратын 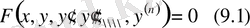теңдігі дифференциалдық
теңдеу деп аталады.
Осы (9.1) теңдеуге кіретін ізденетін функцияның ең жоғарғы ретін
дифференциалдық теңдеудің реті деп аталады.
Кез келген функция 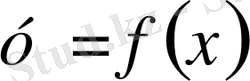дифференциалдық теңдеуге қойғанда оны тепе -
теңдікке айналдырса онда осы функция дифференциалдық теңдеудің шешімі деп
аталады.[kgl]

[gl]§2. Бірінші ретті дифференциалдық теңдеулер.[:]
Егер (9.1) теңдеуіңде n=1 болса , онда 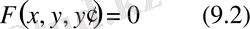теңдеуі бірінші ретті
дифференциалдық теңдеу болады.
Немесе туындысы бойынша анықталған болса онда теңдеу мына 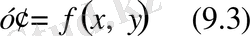түрінде
жазылады.
Теорема. Егер 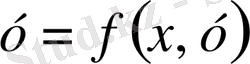функциясы аймағында анықталған, үзіліссіз және
оның үзіліссіз дербес 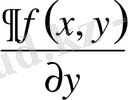туындысы болса, онда х0 нүктесінің -
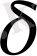маңайы, яғни 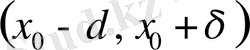табылып, теңдеудің бастапқы шарты қанағаттандыратын ,
яғни егер шешімі бар және ол жалғыз болады.
Егер кез келген тұрақты С үшін 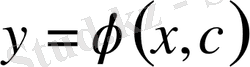функция бірінші ретті теңдеуді
қанағаттандыратын болса онда осы функцияны дифференциалдық теңдеудің жалпы
шешімі деп аталады.[kgl]

[gl]§3. Бірінші ретті дифференциалдық теңдеулер және олардың шешу
жолы.[:]
1. Айнымалылары бөлінген теңдеулер. 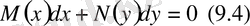бірінші ретті, айнымалылары
бөлінген дифференциалдық теңдеу деп аталады.
Енді (9.4) теңдеудің екі жағын интегралдап теңдеудің жалпы интегралын
табамыз:
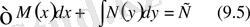
Мысал: 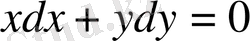дифференциалдық теңдеудің жалпы шешімін табайық.
Шешімі: (9.5) формуланы қолданып 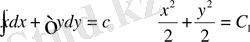немесе
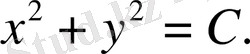
2. Айнымалылары бөлінетін теңдеулер. 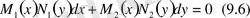теңдеуі бірінші ретті
айнымалылары бөлінетін дифференциалдық теңдеу деп аталады.
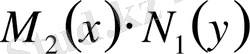көбейтіндісіне боліп (9.4) теңдеудің түріне келтіреміз: 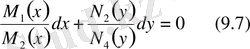. Енді
осы теңдеудің екі жағын интегралдап жалпы интегралын табамыз:
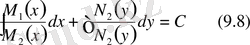
Мысал: xdy-ydx=0 дифференциалдық теңдеуді шешіңіз.
Шешімі: Бұл теңдеу (9.6) теңдеулер түріне жатады. Сондықтан теңдеудің екі
жағын (ху) көбейтіндісіне бөлеміз, сонда 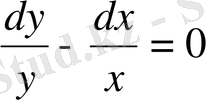теңдеуге келемізде жалпы
шешімін табамыз:
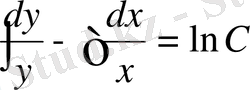
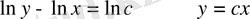
3. Біртекті дифференциалдық теңдеулер. Айталық 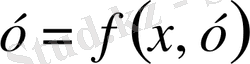функциясы берілген.
Егер кез t нақты саны үшін 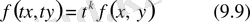теңдігі орындалатын болса, онда
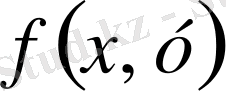функцияны к-ретті біртекті функция деп атайды.
Егер 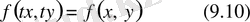теңдігі орындалса, онда 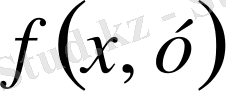функциясы нөлінші ретті біртекті
функция болады. 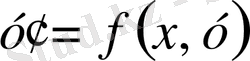(9.11) теңдеуі бірінші ретті біртекті
дифференциалдық теңдеу деп аталады, егер 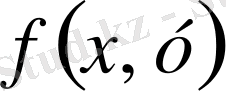функцияға (9.10) теңдігі
орындалса. Бұл теңдеудің шешімін анықтау үшін айнымалыларына ауыстыру
жасаймыз.
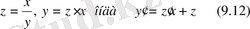
(9.11)-ші теңдеуден 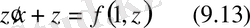айнымалары бөлінетін теңдеуге келеміз.
Мысал: 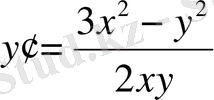дифференциалдық теңдеудін шешімін табыңыз. Шешімі: (9.12)
ауыстыруын қолданып 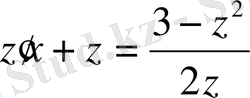теңдеуіне келеміз. Айнымалары бөлінгеннен кейін
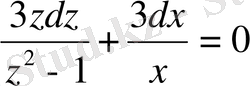теңдеуге келеміз. Осы теңдеудің екі жағын интегралдап
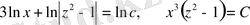ескі айнымаларға қайтып келгенде, жалпы шешімі 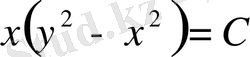түрінде
шығады.[kgl]

[gl]§4. Бірінші ретті сызықты дифференциалдық теңдеу.[:]
Ізделінетін 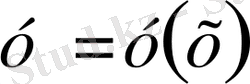функциясы және оның туындысы арқылы сызықты болатын,
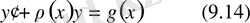теңдеуі бірінші ретті сызықты дифференциалдық теңдеу деп аталады.
Егер 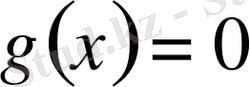онда 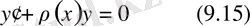біртекті сызықты дифференциалдық теңдеу, егер
g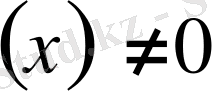текті емес біртекті емес сызықты дифференциалдық теңдеу деп
аталады.
(9.14) теңдеудің шешімін анықтау үшін, теңдеудің шешімін 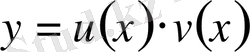(9.16)
түрінде іздейміз. Осы теңдіктен табамыз
(9.16) және (9.17 ) біерілген (9.14) теңдеуіне қоямыз, онда ол түрін
қабылдайды. Бір теңдеуден екі айнымалыны табуға болмайды сондықтан
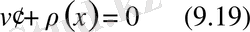деп аламыз. Бұл теңдеу айнымалылары бөлінетін теңдеу. Сондықтан
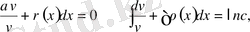
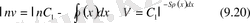
Енді v-ның (9.19) теңдеуіне қоямыз: 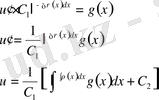(9.21)
Енді (9.16), (9.20) және (9.21) теңдіктерін қолданып (9.15) дифференциалдық
теңдеудің жалпы шешімін анықтаймыз .
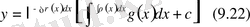Мысал: 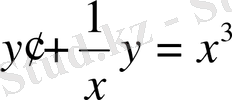бірінші ретті дифференциалдық теңдеудің шешімін табыңыз.
Шешімі: Жоғарыда келтірілген тәсіл бойынша 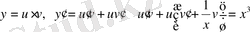түріне келе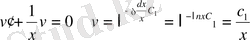ді енді
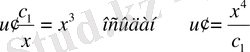
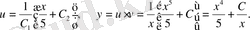Осы анықталған 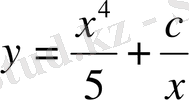берілген теңдеудің жалпы
шешімі болады.[kgl]

Ү. Үйге тапсырма беру

Үйге Данко «Высшая математика» оқулығы бойынша тапсырмалар беру.

Оқытушы: Абдуллаева Х.С.