Айналу денелері: конус, цилиндр және шар - 9-сыныпқа арналған ашық сабақ


№ 4 орта мектебі
Ашық сабақ
«Айналу денелері: конус, цилиндр, шар»
9 «А» сыныбы
Математика пәні мұғалімі:
Ағадиева Қ. И.
Шалқар қаласы
Күні: 15. 03. 2013 ж.
Сыныбы: 9 «А»
Сабақ тақырыбы: «Айналу денелері. Конус, цилиндр, шар»
Сабақ мақсаты:
Білімділік: Оқушыларға конус, цилиндр, шар және олардың элементтері туралы
мағлұматтар беру;
Дамытушылық: Конустың, цилиндрдің, шардың бүйір бетінің, толық бетінің
аудандарын табуға есептер шығарту арқылы оқушылардың
шапшаңдық қабілеттерін дамыту;
Тәрбиелік: Оқушыларды ұйымшылдыққа, нақты пәнге қызығушылыққа,
жауапкершілікке, өзін-өзі тәрбиелеуге баулу;
Сабақ түрі: Жаңа сабақ
Сабақтың әдісі: Сұрақ - жауап, есептер шығару
Сабақтың көрнекілігі: Дербес компьютер, диапроектор, сызба плакаттар, т. б.
Сабақ барысы:
І. Ұйымдастыру кезеңі.
Оқушылармен сәлемдесу;
Оқушыларды түгелдеу;
Назарларын сабаққа аудару;
Оқу - құралдарын түгелдеу.
ІІ. Үй тапсырмасын сұрау, бекітіп қорытындылау
Үй тапсырмасын оқушылардан сұрақ қою арқылы тексеремін.
Жауаптары:
- Стереометрия - кеңістіктегі геометриялық фигуралардың қасиеттерін зерттейтін геометрияның бөлімі.
- Тік бұрышты үшбұрыштың гипотенузасынығ квадраты катеттерінің квадраттарының қосындысына тең болады.
- Шеңбердің радиусы дегеніміз - шеңбер центрі мен оның кез-келген нүктесін қосатын кесінді.
- Шеңбердің диаметрі дегеніміз - центр арқылы өтетін шеңбердің кез-келген екі нүктесін қосатын кесінді.
- Тіктөртбұрыш дегеніміз - барлық бұрыштары тік болатын және ені мен ұзындығы болатын төртбұрыштың бір түрі.
ІІІ. Жаңа сабақты меңгерту.
 Анықтама:
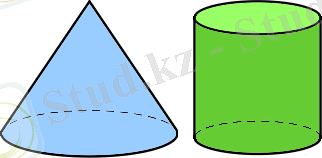
Тікбұрышты үшбұрышты катетінен айналдырғанда шығатын фигура
конус
деп аталады.
Анықтама:
Тікбұрышты үшбұрышты катетінен айналдырғанда шығатын фигура
конус
деп аталады.
Конустың түрлері

Табаны дөңгелек болып келетін және оның биіктігінің табаны дөңгелектің центріне дәл түсетін конусты тік дөңгелек конус деп атаймыз.
Тік емес конустар мектеп курсында қарастырылмайды. Бұл конус айналу денесі болмайды.
Конустың қималары

1 - сурет - Жазықтық конустың табанын хорда бойымен, ал бүйір бетін екі жасаушы бойымен қиып өтеді. Қима - тең бүйірлі үшбұрыш
2 - сурет - Жазықтық конустың осі арқылы өтсе, онда қимада пайда болған үшбұрыш конустың осьтік қимасы деп аталады. Қима - үшбұрыш
3 - сурет - Конусыты оның осіне перендикуляр жазықтықпен қиюға болады. Бұл жағдайда қиюшы жазықтық табан жазықтығына параллель, ал конустың қимасы - дөңгелек
4 - сурет - Конустың жасаушысы арқылы өтетін, конуспен ортақ нүктелері жоқ жазықтық конусқа жанама жазықтық деп аталады.
Негізгі формулалар
Конустың бүйір бетінің ауданы оның табан шеңберінің ұзындығы мен жасаушысының көбейтіндісінің жартысына тең:
Анықтама: Тіктөртбұрышты оның бір қабырғасынан айналдырғанда алынған геометриялық денені тік цилиндр дейміз.

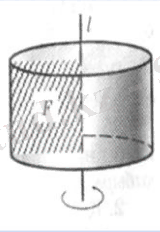
Егер цилиндрдің жасаушылары табандарына перпендикуляр, яғни цилиндрдің биіктігіне тең болса, онда цилиндр тік дөңгелек цилиндр деп аталады.
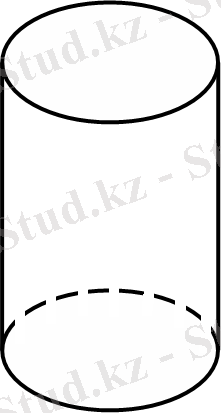 Егер цилиндрдің жасаушылары табандарына қандай да бір а бұрыш жасап көлбеген болса, онда цилиндрді
көлбеу цилиндр
деп аталады.
Егер цилиндрдің жасаушылары табандарына қандай да бір а бұрыш жасап көлбеген болса, онда цилиндрді
көлбеу цилиндр
деп аталады.
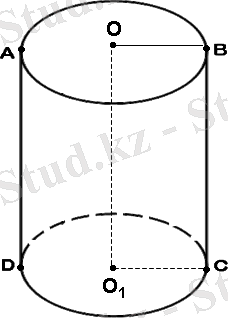
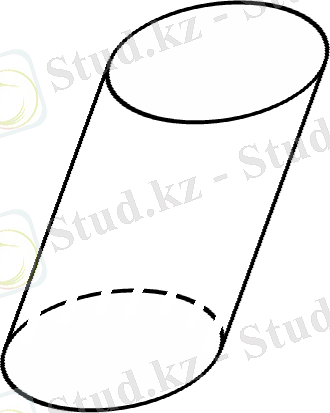
Негізгі формулалар
Анықтама: Жарты дөңгелекті оның диаметрінен айналдырғанда шыққан геометриялық дене шар деп аталады.
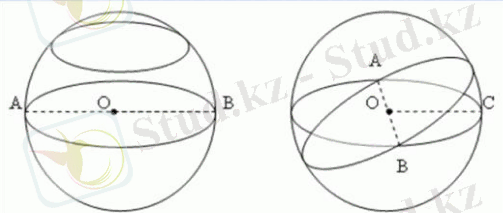
Негізгі формулалар
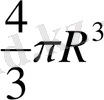
ІV. Жаңа сабақты бекіту
Есептер шығарту
№1 есеп
Конустың жасаушысы 12 дм және табан жазықтығына 30 0 бұрышпен көлбеген. Конустың биіктігін табыңыз.
Sin30 0 =H/L, 1/2= H/12, H=6, Жауабы: 6 (дм)
№2 есеп
Конустың биіктігі 20 см, табанының радиусы 15 см. Бүйір бетінің ауданын табыңыз.
S к. б. б. =ПRL
L 2 = H 2 + R 2 = 400 + 225 = 625, L= 25см
S к. б. б. =П* 15* 25 = 375 П см 2 , Жауабы: 375 П см 2
№3 есеп
Конустың жасаушысы 5 см, табанының радиусы 4 см. Толық бетінің ауданын табыңыз.
S к. тол. беті =ПRL + ПR 2
S к. б. б. =П * 4 *5 = 20 П,
S таб =П * 4 2 = 16П
S к. тол. беті = 20П + 16П = 36П Жауабы: 36П (см 2 )
№4 есеп
D=12 см Шешуі: S т. б = 2ПRH + 2П R 2
H= 3, 5 см R = D/2 = 12/2 = 6см
т/к: S т. б =? S ц. бб = 2ПRH=2П*6*3, 5=42П (см 2 )
S т =2П R 2 = 2П*6 2 = 72П (см 2 )
S т. б = 2ПRH + 2П R 2 = 42П + 72П = 114П см 2
Жауабы: 114П см 2
V. Бос ұяшықты толтыр
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz