Дискретті кездейсоқ шамалар

Сабақ тақырыбы
Дискретті кездейсоқ шамалар
Үздіксіз кездейсоқ шама ұғымы
Осы сабақта қол жеткізілетін оқу мақсаттары (оқу бағдарламасына
сілтеме)
10.3.2.10 дискретті және үздіксіз кездейсоқ шамалардың анықтамаларын біледі және олардың түрлерін ажыратады;
10.3.2.11 кейбір дискретті кездейсоқ шамалардың үлестірім заңдылықтарының кестесін құрады
Сабақ мақсаты
Дискретті және үздіксіз кездейсоқ шамалардың анықтамалары
Істей алады: кейбір дискретті кездейсоқ шамалардың үлестірім заңдылықтарының кестесін құруды біледі
Бағалау критерийлері
- дискретті және үздіксіз кездейсоқ шамалардың ажырата білуді үйрену;
- дискретті кездейсоқ шамалардың үлестірім заңының анықтамасын білу;
- дискретті кездейсоқ шамалардың үлестірім қатарын құра білу.
Тілдік мақсаттар

Пәнге қатысты сөздік қор мен терминдер: Теру/комбинация, орын алмастыру, n-нен r элемент таңдау, орналастыру, рет, реттеу, орын ауыстыру.
Диалогта қолданатын сөз тіркестері мен фразалар: Сіз оларды ...әртүрлі тәсілмен ұйымдастыра аласыз, себебі ..., Кездейсоқ шаманың таралу заңдылығы...., Берілген оқиғаның ықтималдылығы... .
Қойылатын сұрақтар: Кездейсоқ оқиғалар түрінің кездейсоқ шамаларға әсері қандай? Кездейсоқ оқиғалар мен кездейсоқ шамалардың айырмашылығы қалай түсіндіруге болады?
Құндылықтарды
дарыту

- өмір бойы оқыту (сабақтың бүкіл мазмұны ойынша);
- жауапкершілік, сыйластық (топтық жұмыс арқылы);
- адалдық (топтағы бір-бірін бағалау арқылы);
- үштілдік (сабақ мазмұны арқылы);
- әрекеттестік, шыдамдылық(топтық жұмыс, сабақ мазмұны арқылы);
- денсаулық (кабинеттің санитарлық жағдайы).
Пәнаралық байланыстар
Математика, экономика
АКТ қолдану дағдылары
Интерактивті тақтаның мүмкіндіктері, Интернет ресурстары.
Алдыңғы білім

Оқиғаның түрлері 8 сыныптан таныс;
Элементар және элементар емес оқиғалар, классикалық ықтималдық 9 сыныптан таныс.
Саралау
Тапсырмалардің дұрыс орындалун қадағалап, кері байланыс беріледі. Тапсырмалар талқыланып, талданады. Түзетулер жүзеге асады.
Бағалау
Мадақтау, талқылау, ИНСЕРТ
Ресурс
Видео, мәтін(кітаптағы), статистикалық материалдар
Сабақ барысы
Жоспарлан
ған сабақ кезеңдері
Сабақта жоспарланған жұмыс

Сабақтың басы
2 мин

4 мин

Сәлемдесу.
Ұйымдастыру кезеңі: Раппорт

Ынтымақтастық ахуал туғызу
"Бір қадам алға..." әдісі. Өткен материалдарға байланысты сұрақтар:
1) Оқиға ықтималдығы?
2) Оқиға түрлері? Мысалдар келтір.
3) Ықтималдықтар теориясының формуласы?
4) 1-ден 6-ға дейін ұпайлар саны бар кубик лақтырылды. Алтыдан көп емес ұпайлар санының түсуі.
Сабақтың ортасы
35минут
( Жаңа сабақ)

10 мин

15 мин

10 мин

2 мин
Дискретті және үздіксіз кездейсоқ шамалар
Оқушылардың іс-әрекеті: алынған ақпаратты талдайды, нақтылайды; алдында оқылғанмен, белгілімен салыстырады; (қорытынды жасайды, синтездейді). Негігі сәттер мен анықтамаларды дәптерге жазады.

- Күнделікті өмірде және ғылыми зерттеулерде бізді қызықтыратын шамалар кездейсоқ жағдайларға байланысты әртүрлі мәндерді қабылдауы мүмкін.
1) Бір тәулік ішінде Алматы қаласының перзентханаларында дүниеге келген перзенттер саны;
2) Нысананы дәл көздеп атып түсіргенше атылатын оқтар саны;
3) Артиллериялық снарядтың ұшу қашықтығы;
4) Кез келген өндіріс орнының немесе кез келген жанұяның электр энергиясын пайдалану мөлшері (белгілі бір уақыт бірлігінде, айталық, ай, жыл, т.б.).
Осындай жағдайларда кездейсоқ шамалармен (КШ) жұмыс жасау керек болды.
- Кездейсоқ шама дегеніміз не? (Мәндері кейбір тәжірибенің кездейсоқ нәтижесіне тәуелді болатын, сонымен бірге осы мәндердің әрқайсысы белгілі бір ықтималдықпен іске асатын айнымалы шама).

Мысал 1. Студенттік топта 25 адам бар. Х шамасы - сабақ басындағы аудиториядағы студенттер саны. Оның мүмкін мәндері 0, 1, 2,...,25 сандары.
Әрбір тәжірибеде (сабақ басы) Х шамасы міндетті түрде өзінің мүмкін болатын мәндерінің бірін қабылдайды, яғни Х = 0, Х = 1, ..., Х = 25 оқиғаларының біреуі орын алады.

Мысал 2. Кейбір мекеменің акция курсын өлшеу. Мүмкін болатын оқиғалар: Y акциясының құны 0 мен infinity арасындағы бір мәнді қабылдайды.

Мысал 3. Ойын сүйегі бір рет лақтырылды. Мүмкін болатын оқиғалар: жоғарғы жағында Z: 1, 2, 3, 4, 5, 6 сандарының түсуі.

Қорытынды: Кездейсоқ шама жеке мән немесе кейбір аралықтағы мәнді қабылдауы мүмкін. Осыған байланысты кездейсоқ шамалар дискретті және үздіксіз болып бөлінеді.

Кездейсоқ шамаларды екі үлкен топқа - дискретті (ДКШ) және үздіксіз (ҮКШ) бөлуге болады.
ДКШ үшін кездейсоқ шаманың қабылдай алатын мәндерін алдын ала көрсетуге болады, ал ҮКШ үшін барлық мәндерді алдын ала көрсетуге болмайды.

Дискретті КШ - бұл мәндері жеке дара тиянақты сандар болатын айнымалылар.
Мысал: журналдағы бағалар, емтихандағы адам саны.
Үздіксіз КШ - мәндері үзіліссіз белгілі бір аралықта кез келген мәнді қабылдай алатын кездейсоқ шамалар.
Мысал: әртүрлі адамдармен анықталған немесе әртүрлі инструменттерді қолданғандағы бір тек бір бөлшектің өлшемдері.

Дискретті кездейсоқ шаманың үлестірім заңы.
- Дискретті кездейсоқ шамаға тоқталайық. Дискретті кездейсоқ шаманың мүмкін мәндеріне өздерінің ықтималдықтары сәйкес болуы керек.

Анықтама. Кездейсоқ шаманың қабылдайтын мәндері мен олардың ықтималдықтары арасындағы сәйкестікті көрсетіп жазуды дискретті кездейсоқ шаманың үлестірім заңы деп атайды.

Дискретті кездейсоқ шаманың үлестірім заңының берілу түрлері:
:: кесте,
:: аналитикалық,
:: графиктік.

Дискретті кездейсоқ шаманың үлестірім заңының кестелік берілуінде кестенің бірінші жолында барлық мүмкін мәндер, ал екінші жолында - олардың ықтималдықтары болады.
Кестені үлестірім қатары деп атайды.
X
x1
x2
...
xn
хi
P
p1
p2
...
pn
1

- Кездейсоқ шаманың үлестірім қатарын құруға есептер қарастырайық.

1-тапсырма
Жеке жұмыс. Ауызшы есепте.
1 есеп. Кездейсоқ шаманың түрін анықтаңдар.
* Станоктың авариясыз жұмыс істеу уақыты.
* Арақашықтық бірлігіне жұмсалған жағармай.
* Топтағы студенттер саны.
* Ойын сүйегін бір рет лақтырамыз? Екі рет? n рет?
* Бір сөткедегі жауын-шашын мөлшері.
* Нысанаға ату.
* Қарау кезіндегі аурудың температурасын өлшеу.
Дескриптор:
- Кездейсоқ шамалардың түрін анықтайды, талдау және дискуссия кезінде аққатқа көз жеткізеді.

2-тапсырма
Топтық жұмыс. Есептер шығару.
Есеп 2. Өнімді шығару барысында басқару пультында 3 индикатор бар, олар сәйкесінше белгілі операцияға жауап беретін құрылғы істен шыққанда жанады. Индикаторлардың жану ықтималдықтары сәйкесінше тең p1=0,05; p2=0,1; p2=0,2. X - істен шыққан индикаторлар саны, осы кездейсоқ шаманың үлестірім заңын құрыңдар.
Шешуі. X - істен шыққан приборлар саны, олардың келесі мүмкін мәндері болады:
- барлық үш прибор да істен шықпайды;
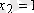- бір прибор істен шығады;
- екі прибор істен шығады;
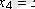- үш прибор істен шығады.
Осы мәндерге сәйкес ықтималдықтарды табайық. Есеп шарты бойынша, приборлардың істен шығу ықтималдықтары тең: p1=0,05; p2=0,1; p2=0,2 . Онда приборлардың гарантия уақытында істен шықпауының ықтималдықтары тең:

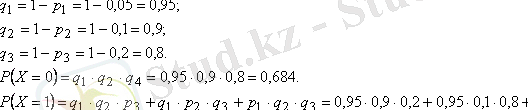
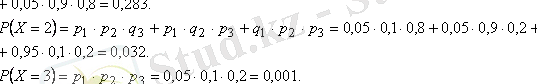
Үлестірім заңы келесі түрде болады:

0
1
2
3
Қосынды

0,684
0,283
0,032
0,001
1

Тексеру: Ықтималдықтар қосындысы 1-ге тең болуы керек.

Есеп 3. Партиядағы 100 бұйымның ішінде 90- ы ақаусыз. Кездейсоқ 3 бұйым алынады. Ақаусыз бұйымдар саны кездейсоқ шамасының үлестірім заңы қатарын құрыңдар.

Шешуі:

0
1
2
3
Қосынды

0,00074
0,025
0,248
0,727
1

100-ден 3 бұйымды таңдаудың барлық мүмкін нұсқалары:
n=C1003=100!3!97!=98∙99∙1001∙2∙3=9702006=161700
m0=C900C103=120, р0=120/161700=0,00074
m1=C901C102=4050, р1=450/161700=0,025
m2=C902C101=40050, р2=40050/161700=0,248
m3=C903C100=117480, р0=117480/161700=0,727

Есеп 4. 1000 лотерея билеті шығарылған: олардың 5-не 500 теңге ұтыс, 10 - на - 100 теңге ұтыс, 20-на - 50 теңге ұтыс, 50- не - 10 теңге ұтыс шығады. Бір билетке ұтыс шығатын X кездейсоқ шамасының үлестірім заңын анықтаңдар.
Шешуі: Есеп шарты бойынша X кездейсоқ шамасының мүмкін мәндері келесідей: 0, 10, 50, 100 и 500.
Ұтыссыз билеттер саны 1000 - (5+10+20+50) = 915, онда P(X=0) = 915/1000 = 0,915. Дәл осылай басқа ықтималдықтарды табамыз: P(X=0) = 50/1000=0,05, P(X=50) = 20/1000=0,02, P(X=100) = 10/1000=0,01, P(X=500) = 5/1000=0,005. Алынған заңды кесте түрінде жазамыз:
xi мәндері
0
10
50
100
500
pi ықтималдықтары
0,915
0,05
0,02
0,01
0,005
Дескриптор:
oo Х кездейсоқ шамасының қабылдайтын мүмкін мәндерінің сәйкес ықтималдықтарын таба алады;
oo Х кездейсоқ шамасының үлестірім заңын құра алады.
3-тапсырма
Тест
1. Дискретті кездейсоқ шаманы табыңыз.
A. Желдің жылдамдығы
B. Бір жылдағы жауын-шышын мөлшері
C. Тянь-Шань тауының Тәңір-Тау жотасындағы Хан-Тәңірі шыңының биіктігі
D. Тоғызқұмалақ ойынында жеңген ойындардың саны
1. Үзіліссіз кездейсоқ шаманы табыңыз.
A. Оқыған әдебиеттердің саны
B. Бір жылдағы жауын-шышын мөлшері
C. Тянь-Шань тауының Тәңір-Тау жотасындағы Хан-Тәңірі шыңының биіктігі
D. Тоғызқұмалақ ойынында жеңген ойындардың саны
* Дискретті кездейсоқ шамасының үлестірім заңы дегеніміз не?
* Дискретті кездейсоқ шамасының үлестірім заңын қандай жолдармен беруге болады?
* Дискретті кездейсоқ шамасының үлестірім қатары дегеніміз не?
Дескриптор:
oo Жаңа өтілген тақырыпқа қатысты материалдарды меңгеріп алды.
Кері байланыс
Оқушы
Жетістік
Кедергі
Түзету
1-тапсырма

2-тапсырма

3-тапсырма

Нәтиже

Сабақ соңы
2 мин
Рефлексия
Оқушылар рефлексия жүргізеді:
- мен нені білдім;
- мен нені түсінбедім;
- маған немен жұмыс жасау керек.
Үй жұмысы:
№1. X кездейсоқ шамасы 0; 1; 2; 3 мәндерін қабылдайды. Ықтималдықтары тең екені белгілі. X дискретті кездейсоқ шамасының үлестірім қатарын жаз.
№ 2. Партияда 10% стандартты емес бөлшектер бар. Кездейсоқ екі бөлшек алынған. Таңдалып алынған бөлшектер ішіндегі стандартты бөлшектер саны - Z, осы дискретті кездейсоқ шамасының үлестірім қатарын жаз.
Саралау - оқушыларға көбірек қолдау көрсетуді қалай жоспарлайсыз? Қабілеті жоғары оқушыларға қандай міндет қоюды жоспарлап отырсыз?
Бағалау - оқушылардың материалды меңгеру деңгейін тексеруді қалай жоспарлайсыз?
Сабақ бойынша рефлексия

Сабақ мақсаттары/оқу мақсаттары дұрыс қойылған ба? Оқушылардың барлығы ОМ қол жеткізді ме?
Жеткізбесе, неліктен?
Сабақта саралау дұрыс жүргізілді ме?
Сабақтың уақыттық кезеңдері сақталды ма?
Сабақ жоспарынан қандай ауытқулар болды, неліктен?
Бұл бөлімді сабақ туралы өз пікіріңізді білдіру үшін пайдаланыңыз. Өз сабағыңыз туралы сол жақ бағанда берілген сұрақтарға жауап беріңіз .

Жалпы баға
Сабақтың жақсы өткен екі аспектісі (оқыту туралы да, оқу туралы да ойланыңыз)?
1:

2:

Сабақты жақсартуға не ықпал ете алады (оқыту туралы да, оқу туралы да ойланыңыз)?
1:

2:

Сабақ барысында сынып туралы немесе жекелеген оқушылардың жетістік/қиындықтары туралы нені білдім, келесі сабақтарда неге көңіл бөлу қажет?