Жазықтықтағы екі нүктенің арақашықтығы

Мектеп: № 266 мектеп-лицей
Мерзімі:25.02.2019
Мұғалімнің аты-жөні:Ізбасар Лаура Разаққызы
Сынып: 10 <<в>>
Қатысқандар саны:
Қатыспағандар саны:
Сабақ тақырыбы:
Екі нүктенің арақашықтығы
Сабақтың түрі:
Онлайн сабақ ZOOM
Осы сабақта қол жеткізілетін оқу мақсаттары (оқу бағдарламасына сілтеме)
10.4.7 - кеңістіктегі екі нүкте арасындағы арақашықтықты таба білу;
10.4.12 - кеңістіктегі вектордың координаталарын және ұзындығын таба білу;
Ойлау дағдысы
Қолдану. Жоғары деңгей дағдылары
Сабақтың мақсаты
Барлық оқушыларға:
- екі нүкте арасындағы арақашықтық формуласын біледі
- екі нүкте арасындағы арақашықтық формуласын табады
Көпшілігі:
- екі нүкте арасындағы арақашықтықтың, нүктелерді қосатын кесіндінің ортасының координаталарын табу формулаларын колданады
Кейбіреуі:
- екі нүкте арасындағы арақашықтық формуласы пайдаланып сызбаларды дайындайды,практикалық есептерді шешеді
Бағалау критерийі
- екі нүкте арасындағы арақашықтықтың сызбаларды дайындайды
- шешу алгоритмдерін құрады
- практикалық есептерде пайдаланады

Тілдік мақсаттар
Пәндік лексика және терминология
- нүктелердің арақашықтығы;
- фигураның орта сызығы;
- параллелограммның қасиеттері;
- нүктелерді қосатын кесіндінің ортасының координаталары;
Диалогқа/жазылымға қажетті тіркестер
-кеңістіктіктегі нүктелердің арақашықтығы........
-Пифагор теоремасы бойынша....
-нүктенің ординатасы,абциссасы,аппликатасы....
-кесіндінің ортасының координатасы.....

Құндылықтарға баулу
Жалпыға бірдей еңбек қоғамы
Пәнаралық байланыстар
Алгебра <<Мәтінді есептерді шығару>>, <<Қысқаша көбейту формуласы>>
Алдынғы білім
Векторды үш компланар емес вектор бойынша жіктеу
Сабақ барысы
Сабақтың жоспарлнаған кезеңдері
Сабақтағы жоспарланған жаттығу түрлері
Ресурстар
Сабақ басы
5 мин

Сабақтың ортасы

20 мин

Сабақтың
соңы
5 мин

Ұйымдастыру кезеңі

-ZOOM конференциясын ұйымдастыру;
-оқушылармен, қатысушылармен амандасу;
-сабақтың мақсатымен таныстыру

Тақырып: Екі нүктенің арақашықтығы
Анықтама. Екі нүктенің арақашықтығы -- екі нүктені қосатын кесіндінің арақашықтығы.
Екі нүктелердің арақашықтығы келесі формуламен өрнектеледі:
Екі нүктелердің арасындағы арақашықтық кесесі формуласымен өрнектеледі A(xa, ya) и B(xb, yb) жазықтықтағы нүктелер:
AB = √(xb - xa)2 + (yb - ya)2
Кеңістіктегі A(xa, ya, za) и B(xb, yb, zb) нүктелелерінің арақашықтығы:(х-абсцисса,у-ордината, z-аппликата)
AB = √(xb - xa)2 + (yb - ya)2 + (zb - za)2
Жазықтықтағы екі нүктелерінің арақашықтығын есептеу формуласын қортып шығару

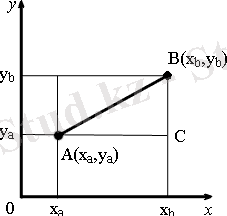
A и B нүктелерінен координаталық осьтеріне перпендикуляр түзулер жүргіземіз.
∆ABC тікбұрышты үшбұрышты қарастырсақ. Катеттері:
AC = xb - xa;
BC = yb - ya.
Пифагор теоремасын қолданып , AB кесіндісінің үзындығын есептейміз :
AB = √ AC2 + BC2.
AC и BC кесінділерінің мәндерін өрнектің орнына қойсақ, жазықтықтағы екі нүктелердің арасындағы арақашықтық формуласы:
AB = √(xb - xa)2 + (yb - ya)2
A (ХА;УА;ZА), В (Хв;Ув;Zв) нүктелерін қосатын кесіндінің ортасының координаталары формуласы:
(ХА+Хв2; УА+Ув2;ZА+Zв2)

Екі нүктенің арақашықтығын есептеу формуласын қолдану мысалдары
Жазықтықтағы екі нүктенің арақашықтығы
1.Есеп
Екі нүктенің арақашықтығын есептеңіз: A(-1, 3) и B(6,2).
Шешуі.
AB = √(xb - xa)2 + (yb - ya)2 = √(6 - (-1))2 + (2 - 3)2 = √72 + 12 = √50 = 5√2
Жауабы: AB = 5√2.
2.Есеп
Екі нүктенің арақашықтығы: A(0, 1) и B(2,-2) ?.
Шешуі.
AB = √(xb - xa)2 + (yb - ya)2 = √(2 - 0)2 + (-2 - 1)2 = √22 + (-3)2 = √13
Жауабы: AB = √13.

Кеңістіктегі екі нүктенің арақашықтығы
3.Есеп
A(-1, 3, 3) и B(6, 2, -2) нүктелер арасындағы арақашықтық?.
Шешуі.
AB = √(xb - xa)2 + (yb - ya)2 + (zb - za)2 =

= √(6 - (-1))2 + (2 - 3)2 + (-2 - 3)2 = √72 + 12 + 52 = √75 = 5√3
Жауабы: AB = 5√3.
4.Есеп
A(0, -3, 3) и B(3, 1, 3) нүктелері арасындағы арақашықтық?
Шешуі.
AB = √(xb - xa)2 + (yb - ya)2 + (zb - za)2 =

= √(3 - 0)2 + (1 - (-3))2 + (3 - 3)2 = √32 + 42 + 02 = √25 = 5
Жауабы: AB = 5.
Екі нүктенің арақашықтығын есептеу
Жазықтықтағы екі нүктенің арақашықтығы
1.Есеп - <<А>>
Үшбұрыш төбелерінің координаталары берілген :А(2;-1;-3), В(-3;5;2), С(-2;3;-5). ВМ - АВС үшбұрышыныің медианасы.ВМ үзындығын табығдар
В(-3;5;2)

М
А(2;-1;-3) С(-2;3;-5)
Шешуі.
АС кесіндісінің ортасы М, М(2-22; -1+32;-3-55)
М(0;1;- 4)
ВМ = (-3-0)2+(5-1)2+(2+4)2=61
Жауабы: BМ = 61.
2.Есеп - <<В>>
АВС үшбұрышыныің орта сызығы МN, М∈ АВ, N∊ ВС. Егер А(-1;3), М(3;4), N(4;2) болса, В, С нүктелерінің координаталарын табығдар
В(хв;ув )
М(3;4) N(4;2)

А(-1;3) С(хс;ус)
Шешуі.
АВ кесіндісінің ортасы М, М(3;4)=(-1+хв2; 3+ув2); В(7;5)
СВ кесіндісінің ортасы N, М(4;2)=(7+хc2; 5+уc2); C(1;-1)

Жауабы: В(7;5), C(1;-1)

3.Есеп - <> №25.19
О
А(2;4;-4), В(1;1;-3), С(-2;0;5), D`-1;3;4) нүктелері параллелограмның төбелері болатынын дәлелдеңдер. В С
оjоООООJ

А D
Шешуі.
АВ = 1-22+1-42+-3+42=11
ВС = (-2-1)2+(0-1)2+(5+3)2=74
CD= (-2+1)2+(0-3)2+(5-4)2=11
АD = (-1-2)2+(3-4)2+(4+4)2=74
AB=CD, ВС=АD
Егер АС және ВD диагональдары бір О нүктесінде киылысу керек:
АС кесіндінің ортасы О(2+(-2)2; 4+02; -4+5)2)=(0; 2; 0,5)
BD кесіндінің ортасы О(1+(-1)2; 1+32; -3+4)2)=(0; 2; 0,5)
Дәлелденді

Рефлексия:
Практикалық есептерді шығару барысында, геометриялық нүктелердің арақашықтығын формулаларын менгергендерін оқушылар Лавыр алқагүліне жапырақтарын қондыру арқылы білдіреді.
Көк түсті-көмек керек, сары түсті-меңгергені
ЖЕҢІС ТАҢБАСЫ-ЛАВР АЛҚАГҮЛІ

Математикада мақсатқа жету үшін, логикалық ойлау қабілеттерін дамыту үшін күнделікті жеке еңбек қажет. Мақсатқа жетудің алғашқы қадамы - үй тапсырмасын уақытылы орындау
Үй жұмысы: 24 параграф.№24.9
Сабақтың соңында математикалық қоржынға қосатын әдемі есептің бірі <<Төсеу және үстінен төсеу>>
Егер кезгелген параллелограмм берілсе, қабырғаларының біреуінің бойынан кезкелген жерден нүкте белгіленіп қарама - қарсы төбелерімен қосылса және тағы бір қабырға бойынан нүкте белгіленіп қарама - қарсы нүктелермен қосылса. Пайда болған жасыл түспен боялған төртбұрыштың ауданы қара түсті бояумен боялған үш фигураның аудандарының қосындысына тең болатынын дәлелде.

Призентация1

Призентация2

Призентация3

Призентация4

Призентация 5

Қосымша ақпарат
Саралау. Сіз қандай тәсілмен көбірек қолдау көрсетпексіз.
Сіз басқаларға қарағанда қабілетті оқушыларға қандай тапсырмалар бересіз
Бағалау. Сіз оқушылардың материалды игеру деңгейін қалай тексеруді жоспарлап отырсыз
Денсаулық және қауіпсіздік техникасын сақтау

Оқушыға дербес қолдау көрсету, оқу материалдары мен ресурстарын оқушылардың жеке қабілеттерін есепке ала отырып, жоспар бойынша қайталау сабақтың ескеріп әдіс-тәсілдерді,тапсырмаларды,ресурстарды саралап жоспарладым. Зерттеу әдісін қолданып лабораториялық-практикалық жұмысты жұргізу барысында оқушылардың өзіндік зерттеу жұмысын жұргізуді қалыптастырамын.
Сабақтың соңында сабақтың ұтымды және осал жақтарын анықтау, түзету мақсатында кері байланыс жасаймын

Тақырыпты қайталау мақсатында оқушылармен практикалық жұмысты ұйымдастырып, формативты бағалаудың дескрипторларын кұрастырдым.

Сабақ басында тақырыпты топтарға таныстыру барысында сынып бөлмесінде жүреді. Сергіту сәтін орындаймын. Компьютермен жұмыстың қауыпсідіқ ережесін сақтайды.
Жалпы баға

Сабақтың жақсы өткен екі аспектісі (оқыту туралы да, оқу туралы да ойланыңыз)?
1.

2.

Сабақты жақсартуға не ықпал ете алады (оқыту туралы да, оқу туралы да ойланыңыз)?

1.

2.
Сабақ барысында сынып туралы немесе жекелеген оқушылардың жетістік/қиындықтары туралы нені білдім, келесі сабақтатарды неге көніл бөлу қажет?