Интеграл

Интеграл. Ньютон-Лейбниц формуласы
Қарағанды қаласы, № 65 орта жалпы білім беретін мектебінің математика пәнінің мұғалімі Омирбекова С.М.
Сабақтың мақсаты: Оқушыларды интегралды есептеу үшін Ньютон-Лейбниц формуласын қолдану бойынша білік, дағдыларын қалыптастыра отырып, білімдерін нақтылау.
Білімділік: Тақырыптың ғылымилығын меңгерту, проблемаларды байқау және оның шешілу жолдарын табу.
Дамытушылық: Ойын арқылы тақырыпты тереңірек меңгеруге бағыт беру
Тәрбиелік: Өз ойын еркін жеткізуге, ой-пікірімен бөлісе білуге, шығармашылыққа ұмтылдыру.
Сабақ әдісі: Сайыс сабақ
Сабақ жоспары:
1.Ұйымдастыру кезеңі .
2.Кім жылдам? Кестені толтыру.
3.<<Ойлан, тап!>> ойыны.
Карточкалардағы тапсырмаларды орындау.
4.Қатесін табыңдар.
5.Зерделілер сайысы. Оқулықтан есептер шығару.
6.Шығармашылық бөлім.
7.Үйге тапсырма
8.Қорытынды
Cабақтың барысы:
І.Ұйымдастыру кезеңі
а) Оқушыларды түгендеу
ә) Сыныпты 4-5 топқа бөлу және сабақтың мақсатымен, ойын шарттарымен таныстыру.
Функция, Өрнек, Интеграл, Алгоритм тағы сол сияқты топ аттарын қояды.
б) Топтардың өздерін таныстыруы
ІІ. Кім жылдам? Кестені толтыру (әр топқа 2 кестеден)

функция

kf(x)

x-3

x-sinx

f(kx+b)

5cos2x

1sin23x

Алғашқы функция

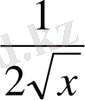
III. <<Ойлан, тап!>> ойыны. Карточкалардағы тапсырмаларды орындау.
Берілген функцияның алғашқы функциясын жазыңдар:
Функция
Алғашқы функция
a)y=-3x+1

b)y=cosx+cos(-x)

c)y=(x-1)2

d)y=4sinx+cos3x

e) y=cos4x- sin4x

f) y=

k)f(x) =

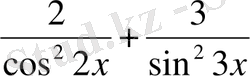
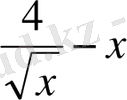
Дұрыс жауабы:
Функция
Алғашқы функция
a)y=-3x+1
F(x)= -3x22+x+C
b)y=cosx+cos(-x)
F(x)=2sinx+C
c)y=(x-1)2
F(x)=x-133+C
d)y=4sinx+cos3x
F(x)= - 4cosx+13sin3x+C
e) y=cos4x- sin4x
F(x)=12sin2x+C
f) y=
F(x)=tg2x-ctg3x+C
k)f(x) =
F(x)=8x-x22+C
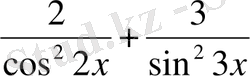
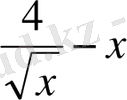
IV.Қатесін табыңдар:
1)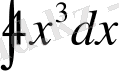=x4+C дұрыс
2) 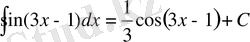дұрыс
3)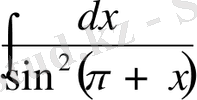=-tgx+C ( қате, дұрыс жауап -ctgx+C )
4) 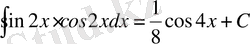дұрыс
V.Зерделілер сайысы.
Оқулықтан есептер шығару:№43(2,3),№44(2,3),45(4)
Шешімдерін дәптер алмастыру арқылы топтар өзара тексереді.
№43
2)01(2x+3)3dx=(2x+3)4810=1854-34=18625-81=68
3) -10dx(6x-1)4=-118(6x-1)30-1=-118-1+73=-118∙342=-1918
№44
2) 412dx2x+1=2x+1124=25-9=2
3)232x3+x2+2x+11+x2dx=23x22x+1+2x+1x2+1dx=232x+1dx=(x2+x)32=12-6=6
№45
4)-3x(4t-1)dt<0
(2t2-t)x-3=2x2-x-(18+3)<0)
2x2-x-21<0
x∈(-3; 3.5)
VI.Шығармашылық тапсырма: функция, алғашқы функция, өрнек, анықталған интеграл, алгоритм, есептеу сөздерін қолданып төрт жол өлең, әңгіме құрастыру керек.
Үйге тапсырма: №41,43(1,4) (І деңгей) №42,44(1,4)(ІІ деңгей)
№44,45(ІІІ деңгей)
Қорытынды. Жеңген топтарды анықтау. Оқушылардың өзін-өзі бағалау парақтарына баға қойғызу және сабақтың әр кезеңін ескере отырып білімдерін бағалау.
Бағалау парағы Топтың аты __________________
Топ мүшесі
Таныстыру
Үй тапсырмасы
Кім жылдам?
Ойлан, тап!
Қатесін тап
Зерделілер сайысы
Жалпы ұпайы