Көрсеткіштік функция, оның қасиеттері мен графигі. 11 сынып

Облыстық дарынды балаларға арналған
интернаттық мекемесі бар ұлттық гимназиясы








Көрнекілік сабақ:
<<Көрсеткіштік функция, оның қасиеттері мен графигі>>


11 <<в>> сыныбы
Алгебра және анализ бастамалары


Математика пәні мұғалімі:
Рамазанов Сағынғали













Сабақтың тақырыбы: Көрсеткіштік функция, оның қасиеттері мен графигі
Сабақтың мақсаты:
Білімділігі: Оқушыларға көрсеткіштік функция, қасиеттері мен графигін салу, көрсеткіштік функцияның қасиеттерін пайдаланып есептер шығару және графигін салу жолдарын түсіндіру. Көрсеткіштік теңдеулерді, теңсіздіктерді және олардың жүйелерін шешуге үйрету;
Дамытушылығы: логикалық ой өрісін, кеңістікте ойлану қабілетін, берілген есептердің шығара білу дағдысын қалыптастыру;
Тәрбиелілігі: математика пәніне деген қызығушылығын, есептертерді шығаруға үйрету.

Құралдар: интерактивті тақта, таблицалар, тест тапсырмалары, өзіндік жұмыс карточкалары.

Сабақтың типі: Іскерлік пен дағдыны қалыптастыру.

Сабақтың әдісі: Деңгейлеп оқыту

Сабақтың жүрісі:
I. Сабақтың тақырыбы мен мақсатын таныстыру

II. Өткен материалдарды қайталау, пысықтау
1. Үй жұмыстарын тексеру (шықпаған есептер бойынша қорытындылау).
2. Ауызша орындайтын жұмыстар:
а) Табица бойынша жұмыс
. 1-таблица
Көрсеткіштік функция
Анықтама. y = ax, где a0, a!=1 түріндегі берілген функцияның көрсеткіштік функция деп атайды.

Қасиеттері
1. Анықталу облысы D(f)

x R (D( ax) = R )
2. Мәндерінің облысы E(f)

y>0 (E( ax) = (;infinity) )
3. Жұп, тақтығы

Функция жұпта емес, тақта емес
4. координат өстерімен қиылысуы
ОХ өсімен қилыспайды, ал ОУ өсімен (; 1) нүктесінде қилысады.
5.Үзіктілігі
Функция барлық анықталу облысында үзіліссіз
6. Таңба тұрақтылығы
Барлығы үшін x R y = ax>0
7. Өсуі мен кемуі
a1 өседі
0< a1
кемиді убывает
8. Көрсеткіштік функцияның графигі
Y


1
Х
0
У

1
0 Х

* Көрсеткіштік функцияның қасиеттерінің көмегімен,
А) m және n сандарын салыстырыңдар, егер төмендегі теңсіздік дұрыс болса: 10m3< 10n3
Ә) х-тің таңбасы қандай: 2,3x=4,5; 0,2x=0,4; 0,7x=2,7; 5,1x=0,23; 0,4x=0,25; 4,3x=3,1.
Б) Сандарды салыстырыңдар: 32 және 33; 12-5және 12-3.
* Төмендегі көрсетілген берілген функциялардың қайсысының графигі болады?

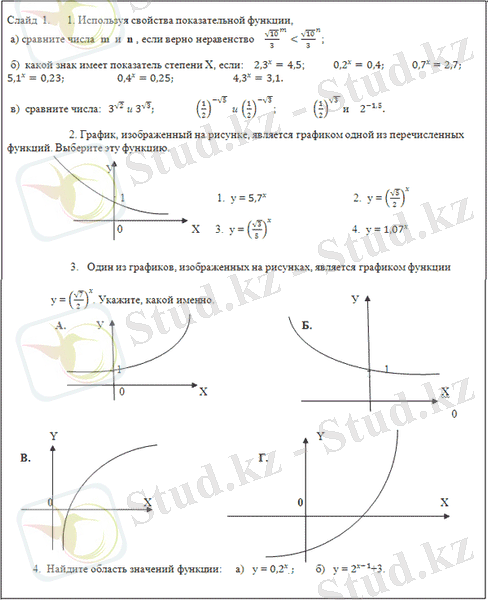
* Төменде берілген графиктердің біреуі y=72xфункциясының графигі, қайсысы екенін көрсет:

* Функцияның мәндерінің облысын табыңдар:
* y=0,2x
* y=2x-1+3

2 таблица.
Көрсеткіштік теңдеулер мен теңсіздіктер

Формулалар
Функция графиктері y = a[x] ( a > 0)
am∙an=am+n
aman=am-n
amn=amn
nam= amn
an∙bn= abn
anbn=abn

ac=b
a>0,a!=1,b>0

⇔
C = logab

a > 1
0 < a < 1
a = 1

Y

1
0 X



өседі

Y

1

0
X

кемиді

У

1

0 Х


тұрақты


Теңдеулер
Теңсіздіктер
a > 0 af(x)=ag(x)

fx=g(x)

X
a !=1 a = 1
a > 0 , a !=1 af(x)>ag(x)

a>1 0
fx
fx>g(x)



III. Өткен материалдарды пысықтау үшін тапсырмалар беріледі:
* Үздік оқушылар карточкаларға жауап береді
* Басқа оқушыларға слайдтарда көрсетілген тапсырмалар беріледі.
* Теңдеулерді шешіңдер:
* Теңсіздіктерді шешіңдер:
* Теңдеуді график бойынша шешіңдер:

1V. Білімді тереңдету
Оқушылар әртүрлі деңгейлі тапсырмаларды өздігінен орындайды:

Қиындатылған есептер:

V. Сабақты қортындылау

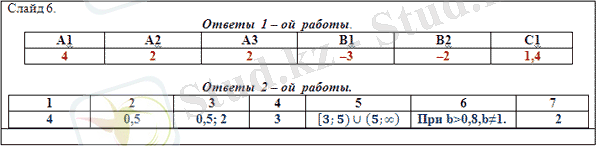
V1. Үй жұмысын беру