Туындының физикалық және геометриялық мағынасы және функцияның графигіне жүргізілген жанама


Қуанышева Сауле Ошақбайқызы
математика пәнінің мұғалімі
Алматы облысы, Ақсу ауданы, Абай орта мектебі мектепке дейінгі шағын орталығымен
Сабақтың тақырыбы: Туындының физикалық және
геометриялық мағынасы. Функцияның графигіне жүргізілген жанама
Сабақтың мақсаты:
1. Оқушыларға туындының физикалық мағынасын және функцияның графигіне жүргізілген жанаманың формуласымен таныстыру.
2. Оқушылардың логикасын, ой-өрісін арттыру, шапшаң есептеуге дағдыландыру.
3. Ұйымшылдыққа тәрбиелеу. Білім алуға ынтасын арттыру.
Сабақтың түрі: жаңа сабақ
Сабақтың көрнекілігі: интерактивті тақта, карточка
Сабақтың барысы:
1. Ұйымдастыру: а) амандасу
ә) түгендау
б) сабаққа әзірлігін тексеру
2. Үй тапсырмасын тексеру
№ 187
3. Жана сабақты түсіндіру
у = f(x) функциясының х нүктесіндегі f′(x) туындысы оның х нүктесіндегі өзгеру жылмадығын анықтайды.
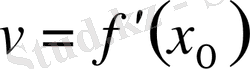
Мысалы: S(t) = 6t 2 - 5t + 4 заңы бойынша түзу сызықты қозғалған дененің t = 1с кезіндегі қозғалыс жылдамдығын тап.
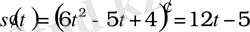
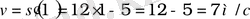 Жауабы: 7м/с
Жауабы: 7м/с
Жылдамдықтан алынған туынды үдеуге тең.
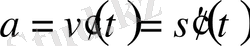
Мысалы: S(t) = 3t 3 - 9t 2 + 6t - 14 заңы бойынша түзу сызықты қозғалған дененің t = 2с кезіндегі дененің үдеуін тап.
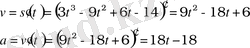
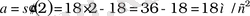 Жауабы: 18м/с
2
Жауабы: 18м/с
2
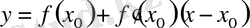 теңдеу жанаманың теңдеуі деп аталады.
теңдеу жанаманың теңдеуі деп аталады.
Мысалы: f(x) = 5x 3 +4x 2 +21x-19 функциясының графигіне абсциссасы х0 = 1 нүктесінде жүргізілген жанаманың теңдеуін жаз.
f(1) = 5⋅13 + 4 ⋅12 + 21 ⋅1 - 19 = 5 + 4 + 21 - 19 = 11
f′(x) = 15x 2 + 8x + 21
f′(1) = 15⋅1 2 + 8⋅1 + 21 = 15 + 8 + 21 = 44
y = 11 + 44(x - 1) = 11 + 44x - 44 = 44x - 33
у = f(x) функциясының х 0 нүктесіндегі туындысы f′(x 0 ) осы функция графигінің (х 0 ; f(x 0 ) ) нүктесі арқылы өтетін жанаманың бұрыштың коэффициетіне немесе бұрыштың тангенсіне тең.
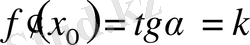
Мысалы: f(x) = 4x 2 - 5x + 6 функциясы графигінің берілген М(1; 2) нүктесінен өтетін жанамасының абсцисса осіне көлбеулік бұрышының тангенсін тап.
f′(x) = 8x - 5
f′(1) = 8 ⋅ 1 - 5 = 8 - 5 = 3
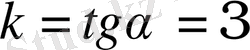
f(x) = 7x 2 + 29x + 6 функциясы графигінің берілген М(-2; 5) нүктесінен өтетін жанамасының абсцисса осіне көлбеулік бұрышын тап.
f′(x) = 14x + 29
f′(-2) = 14 ⋅ (-2) + 35 = -28 + 29 = 1
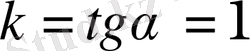
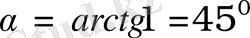
Интерактивті тақтадағы өздік жұмыс тапсырмаларын орындайды.
4. Түсінігін тексеру.
Әр оқушыға карточка таратылады.
5. Сабақты қорытындылау
Бұрыштың тангенсі дегеніміз не?
Жанаманың теңдеуі?
Үдеу дегеніміз не?
6. Үйге тапсырма беру
№193, 197, 198
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz