Мазмұнды есептерді шешу

Мазмұнды есептерді шешу
З.Салыкова
Қ.Топаев атындағы орта мектебі
Математиканы мектепте оқытудың басты мақсаты - қазіргі қоғамның әрбір мүше- сінің күнделікті өмірі мен еңбек қызметіне қажетті аралас пәндерді үйрету мен білім беруді жалғастыруға жеткілікті жүйелі математикалық білімді меңгерген ,икемді, саналы, жеке зерделі оқушыны қамтамасыз ету.
Жаңа техника мен технологияны меңгеріп , басқару үшін алып шығатын жалпы дайындық құрамына сапалы математикалық білім ауадай қажет. Осы мақсаттарды жүзеге асыруда мазмұнды есептердің алатын орны ерекше . Бірақ мазмұнды есептерді шығару оқушыларға қиындық туғызады .
Мазмұнды есептерді шығарудың дайын әдісі жоқ , бірақ та осы есептерді шығару үшін келесі схеманы пайдалануға болады .
1. Белгісіз шамаларды анықтау .
Көп жағдайда белгісіз шама деп есептің шартындағы ізделінді шаманы алған дұрыс. Осы тәсілді ең бірінші кезекте қарастыру керек , бірақ кейде басқа шамалар арқылы теңдеулерді құрастыру жеңіл, оларды тапқаннан кейін, нақты ізделінді шаманы табуға болады .
* Теңдеу құрастыру .
Теңдеулер құрастыру барысында есептің барлық шарттарын пайдаланған жөн . Теңдеулер саны мен белгісіздер саны бірдей болу керек .
3. Ізделінді шаманы табу керек .
Егер бөгде түбірлер пайда болса , онда оларды есептің шартына байланысты алып тастау керек .
Жоғары сынып оқушыларын ҰБТ - ге әзірлеуде өзім қолданып жүрген кейбір мазмұнды есептерді шешу тәсілдерін ұсынып отырмын.
1-есеп Велосипедші бүкіл жолды белгілі жылдамдықпен 2 сағатта жүріп өтуі керек еді. Ол жылдамдығын 3 км/сағ арттырғандықтан,бүкіл жолды 1 сағ жүріп өткен жолдың ұзындығын табыңыз.
А) 28 км ; В)30 км ; С) 25 км ; Д) 32 км ; Е) 35 км .
Шешуі : Велосипедшінің жылдамдығын х км /сағ деп белгілейміз , ал арттырғандағы жылдамдығы ( х + 3 ) км/сағ болады . 2 сағ жүріп өтетін жолы 2х км , ал 1сағ жүретін жолы 1 х км болады . Демек , 2х = 1 ( х + 3 ) теңдеуін аламыз . Енді осы теңдеуді шығарамыз :
2 х = 1 х + 5 , х = 5 , х = 15 . Сонымен , велосипедшінің жылдамдығы 15 км / сағ . Велосипедші осы жылдамдықпен 2 сағ жүріп өтуі керек болғандықтан , бүкіл жолдың ұзындығы
S = 15 2 = 30 км
Жауабы : 30 км
2 -есеп Моторлы қайық ағыспен 12 км , ағысқа қарсы 12 км жүрді. Ағысқа қарсы жүрген жолына ағыспен жүрген жолынан 1сағат артық уақыт жібереді. Қайықтың тұнық судағы жылдамдығы 9 км/сағ болса, ағыс жылдамдығын табыңыз.
А) 1 км / сағ; В) 3,5 км/ сағ ; С) 3 км/ сағ ; Д) 2 км / сағ ; Е) 2,5 км/ сағ
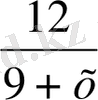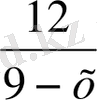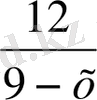
Шешуі : Ағыс жылдамдығын х км / сағ деп белгілейміз. Онда ағыспен жүрген жылдамдығы ( 9 + х ) км /сағ , ал ағысқа қарсы жүрген жылдамдығы ( 9 - х ) км/сағболады . Ағыспен 12 км жолды сағ, ағысқа қарсы 12 км жолды сағ жүреді. Ағысқа қарсы жүрген жолына 1 сағат уақыт артық жұмсайды , сондықтан - 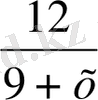= 1 теңдеуін аламыз . 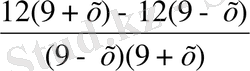= 1, 108 + 12х - 108 + 12х = 81 - х2 ,
24х = 81 - х2 , х2 + 24х - 81 = 0 , Д = 576 + 324 = 900 , х1,2 =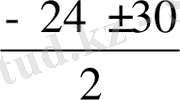, х1 = 3 , х2 = -27. v > 0 болғандықтан , х = 3 км /сағ
Жауабы : 3 км /сағ
3-есеп Екі қаланың арасын қосатын екі түрлі жол бар. Оның біреуінің ұзындығы екіншісінен 10 км артық. Бірінші жолмен автомобиль жүріп келеді, ол екі қаланың арасын жүріп өту үшін 3,5 сағ жұмсайды, ал екінші машина екінші жолмен екі қаланың арасындағы 2,5 сағ жұмсайды. Егер бірінші машинаның жылдамдығы екіншісіне қарағанда 20 км/сағ аз болса, онда машиналардың әрқайсысының жылдамдықтары қандай?
А) 60 км /сағ , 40 км / сағ В) 80 км / сағ, 100 км / сағ С) 75 км / сағ , 95 км / сағ Д) 65 км / сағ , 85 км / сағ Е) 60 км / сағ , 80 км / сағ
Шешуі :

v
t
s
айырмасы
I
х-20
3,5
3,5 (х - 20)
10
I I
х
2,5
2,5 х

3,5 ( х - 20 ) - 2,5 х = 10
3,5 х - 70 - 2,5 х = 10
х - 70 = 10
х = 80
Демек ,екінші машинаның жылдамдығы 80 км / сағ , ал бірінші машинаның жылдамдығы х - 20 = 80 -20 = 60 (км / сағ )
Жауабы : 60 км /сағ , 80 км / сағ
4-есеп Өзен бойындағы екі пристаньның ара қашықтығы 80 км. Қайықтың бір пристаньнан екінші пристаньға барып қайтуына 8 сағ20 мин уақыт кетеді. Ағыс жылдамдығы 4 км/сағ деп есептеп, қайықтың тынық судағы жылдамдығын табыңыз.
А) 21км/сағ В) 18км /сағ С)22км /сағ Д) 19км/сағ Е) 20 км/сағ
Шешуі : Қайықтың тынық судағы жылдамдығы - х км / сағ , ағыспен жүрген жылдамдығы - (х + 4) км / сағ , ағысқа қарсы жүрген жылдамдығы - ( х - 4 ) км / сағ. 80 км жолды ағыспен 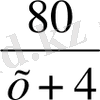сағ , ал ағысқа қарсы 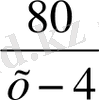сағ жүріп өтеді . Бір пристаннан екінші пристаньға барып қайтуына 8 сағ 20 мин (8 сағ = 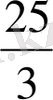сағ ) уақыт кететіндіктен , мына теңдеуді құрамыз :
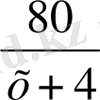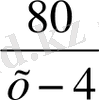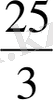+ = , ортақ бөлімі -3 ( х+ 4 ) (х - 4 )
480 х = 25 х[2] - 400 , 25 х2 - 480 х - 400 = 0 , 5х2 - 96х - 80 = 0
Д = 9216 + 1600 = 10816 , х 1,2= 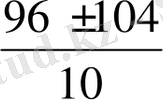, х1= - 0,8 , х2= 20 . Сонымен , v >0 - ден болғандықтан , қайықтың тынық судағы жылдамдығы 20 км / сағ .
Жауабы : 20 км / сағ
5-есеп Пароход өзен ағысымен 3 сағ жүріп өткен жолын ,қайтар жолында 5 сағ жүріп өткен. Өзен ағысының жылдамдығы 5 км/сағ. Пароходтың тынық судағы жылдамдығын табыңыз
А) 20км/сағ В) 15км/сағ С) 5км/сағ Д) 10 км/сағ Е)18км/сағ
Шешуі : х - пароходтың тынық судағы жылдамдығы ,
х + 5 - ағыспен жүрген жылдамдығы
х - 5 - ағысқа қарсы жүрген жылдамдығы
3 ( х + 5 ) км - өзен ағысымен 3 сағ жүріп өткен
жолы
5 ( х - 5 ) км - қайтар жолында 5 сағ жүріп өткен
жолы .
Енді теңдеу құрып шығарамыз : 3 ( х + 5 ) = 5 ( х - 5 )
3 х + 15 = 5 х - 25
2 х = 40
х = 20
Сонымен , пароходтың тынық судағы жылдамдығы 20 км / сағ
Жауабы :20 км / сағ
6-есеп Жұмысшылар бригадасы 360 детальды дайындап шығуы керек еді. Күніне белгіленген жоспардан 4 детальді артық жасағандықтан бригада барлық тапсырманы белгіленген мерзімнен 1 күнге ерте бітірді. Осы тапсырманы орындауға бригада қанша күн жұмсады?
А) 7 күн В ) 9 күн С) 10 күн Д) 8 күн Е) 6 күн
Шешуі : х - жоспар бойынша дайындалатын детальдар саны
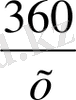- жоспар бойынша тапсырмаға жұмсайтын күні
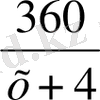- тапсырманы орындауға жұмсаған күні
Бригада барлық тапсырманы белгіленген мерзімнен 1 күнге ерте бітірді , сондықтан , мына теңдеуді аламыз :
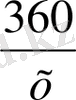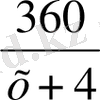- = 1
Енді осы теңдеуді шығарамыз
1440 = х[2] + 4х
х[2] + 4х - 1440 = 0
Д = 16 + 5760 = 5776
х1,2 = 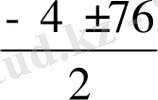, х1 = -40 ( есептің шартын қанағаттындырмайды),
х2 =36 . Сондықтан , х = 36 .

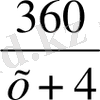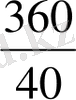= = 9 , демек , бригада тапсырманы орындау үшін 9 күн жұмсады . Жауабы : 9 күн
7-есеп Белгілі жұмысты бір ұста 12 күнде, екінші ұста 6 күнде бітіреді. Екі ұста бірігіп сол жұмысты неше күнде бітіреді?
А) 8 күнде В) 6 күнде С) 5 күнде Д) 4 күнде Е ) 3 күнде
Шешуі: х күн - екі ұста бірігіп бітіретін жұмыс күні
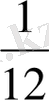- бірінші ұстаның жұмыс өнімділігі
- екінші ұстаның жұмыс өнімділігі
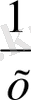- екі ұстаның бірігіп істеген жұмысының
өнімділігі
Енді теңдеу құрамыз : + = , = , = ,
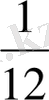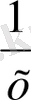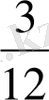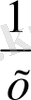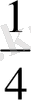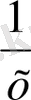х = 4 . Демек , екі ұста бірігіп сол жұмысты 4 күнде бітіреді
Жауабы : 4 күнде
8-есеп Екі құбыр бассейнді 7,5 сағ толтырады. Бірінші құбыр жеке өзі бассейінді екінші құбырға қарағанда 8 сағ бұрын толтыра алады. Бірінші құбыр жеке өзі бассейінді неше сағатта толтырады.
А) 12 сағ В) 14 сағ С) 15 сағ Д) 11 сағ Е) 10 сағ
Шешуі : I құбыр - х сағ , II құбыр - (х + 8 ) сағ толтырады.
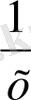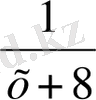( +) 7,5 = 1
7,5 ( х + 8 + х ) = х ( х + 8 )
х2 +8х -15х - 60 = 0
х2 -7х - 60 = 0
Д = 49 + 240 = 289 , х1,2 = 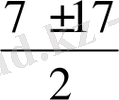, х1 = - 5 , х2 = 12
х1 = -5 есептің шартын қанағаттандырмайды ,демек , х = 12
9-есеп Мыс пен қалайыдан тұратын екі кесек қорытпа бар. Бірінші қорытпада 40% , екіншісінде 32% мыс бар. 35% мысы бар 8 кг қорытпа алу үшін бірге қорытылатын кесектердің салмағы қандай болуы керек?
А) 4 кг ,3 кг В) 1 кг ,7 кг С) 4кг ,4кг Д) 2кг , 6кг Е) 3кг ,5кг
Шешуі : х - бірінші кесектің салмағы , у - екінші кесектің салмағы . Алынған қорытпаның салмағы 8 кг , сондықтан , х+ у =8 . Бірінші қорытпада - 0,4 х кг мыс , екінші қорытпада - 0,32 х кг мыс бар . Алынған қоспада 8 0,35 = 2,8 кг мыс бар.
демек , 0,4 х + 0,32 у = 2,8 , теңдеудің екі жағын да 0,4 - ке бөлеміз.Сонда, х + 0,8 у = 7 теңдеуі шығады . Енді теңдеулер жүйесін құрамыз :
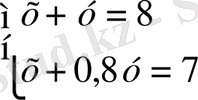
Осы теңдеулер жүйесін шешу үшін (1) теңдеуден (2) теңдеуді аламыз : 0,2у = 1 , у = 5 . Ал х - тің мәнін (1) теңдеуден табамыз: х + у = 8 , х = 8 - у , х = 8 - 5 = 3 . Демек , 8 кг қорытпа алу үшін бірге қорытылатын кесектердің салмағы 3 кг және 5 кг .
Жауабы : 3 кг , 5 кг
10-есеп 36 кг мыс пен мырыш қорытпасының 45% - і мыс. Қорытпада 60% - тік мыс болу үшін , қорытпаға қанша мыс қосу керек ?
А) 13 кг В) 18,2 кг С) 13,5 кг Д) 16,2 кг Е) 15,5 кг
Шешуі: 36 кг қорытпада 36 0,45 = 16,2 кг мыс ,
х кг мыс қосамыз , сонда 16,2 + х болады
Енді мына теңдеуді құрамыз : = 0,6
16,2 + х = 0,6 х + 21,6 , 0,4 х = 5,4 , х = 13,5
Жауабы: 13,5 кг
11-есеп Тауардың бағасын алдымен 20% - ке, ал одан кейін жаңа бағасын тағы да 25% - ке кемітті. Тауардың бастапқы бағасын барлығы неше процентке кеміткен ?
А) 40% В) 43% С) 47% Д) 42% Е)45%
Шешуі: Ап = А0 ( 1 - р1 ) ( 1 - р2 ) ,мұнда Ап - жаңа бағасы , А0 - бастапқы бағасы , р1 , р2 - өзгерген % - ті
Ап = А0 ( 1 - 0,2 ) ( 1 - 0,25 )
Ап = А0 0,6
Сонда , жаңа бағасын 100% - 60 % = 40% - ке кеміткен
Жауабы : 40%
12-есеп Калькулятордың бағасын алдымен 25 % - ке, ал содан соң тағы да 65 % - ке арттырды. Калькулятордың бағасы қанша есе өсті ?
А) 2,2625 В) 1,1625 С) 1,0625 Д) 2,1625 Е) 2,0625
Шешуі : Ап =А0 ( 1 + р1) ( 1 + р2 )
Ап = А0 ( 1 + 0,25 ) ( 1+ 0,65 )
Ап = А0 1,25 1,65
Ап = А0 2,0625
Сонда , калькулятордың бағасы 2,0625 есе өскен .
Жауабы : 2,0625 есе өскен
13-есеп 15 л 10% - тік ерітіндіге 5% - тік тұз араластырып, 8% - тік ерітінді алынды. Қанша 5% - тік ерітінді қосылған?
Шешуі : 15 л 10 % - тік ерітінді - 15 0,1 = 1,5
х - тұз ерітіндісі , 5 % - тік тұз ерітінді - 0,05 х
= 0.08 , 1,5 + 0,05х = 0,08 ( 15 + х )
1,5 + 0,05 х = 1,2 + 0,08 х , 0,03 х = 1,5 -1,2 , 0,03 х = 0,3 ,
х = 10
Жауабы : 10 л
14-есеп Тапсырманы екі жұмысшы бірігіп 12 күнде бітірер еді. Егер олардың біреуі тапсырманың жартысын орындап, қалған жұмысты екіншісі ауыстыратын болса, барлық жұмыс 25 күнде орындалып бітеді. Әр жұмысшы жеке - жеке бүкіл тапсырманы қанша күнде бітірер еді?
А) 35; 25 В) 30 ; 20 С ) 26 ; 24 Д ) 32 ; 22 Е ) 28 ; 18
Шешуі : I жұмысшы - х күнде , ал II жұмысшы - у күнде бүкіл
тапсырманы орындап бітіреді
Барлық жұмысты - 1 деп аламыз
бірінші жұмысшының жұмыс өнімділігі
- екінші жұмысшының жұмыс өнімділігі
Олар бірігіп жұмысты 12 күнде бітірсе , онда
болады . Егер біреуі тапсырманың жартысын орындап , қалған
жұмысты екіншісі ауыстырып 25 күнде бітіретін болса , онда
теңдеуін аламыз. Сонда мына теңдеулер жүйесін аламыз :

Осы теңдеулер жүйесін шешеміз : х = 30 , у = 20
Демек , бірінші жұмысшы тапсырманы 30 күнде , ал екіншісі 20 күнде бітірер еді .
Жауабы : 30 күн , 20 күн

Пайдаланған әдебиеттер :
* Математика . Тест жинағы . Астана . 2004 - 2009 жж
* Ш. А. Алимов, Ю. М. Колягин и другие . Алгебра. Учебник для 8 класса

Қостанай облысы,
Жангелдин ауданы.