Келтіру формулалары. 9 сынып

Скачать

Сабақтың тақырыбы: Келтіру формулалары

Сабақтың мақсаты:

Білімділік: Оқушыларға сүйір бұрыштың тригонометриялық функциясының әрбір бұрышындағы синустыың, косинустың, тангенстің, котангенстің келтіру формулаларымен таныстыру, осы формулаларды тригонометриялық өрнектерді түрлендіруде және есептерді шығару кезінде қолдануды үйрету;

Дамытушылық: Оқушылардың ақыл-ойын дамыту, ойлау қабілетін жетілдіру.

Тәрбиелік: Оқушылардың алгебра пәніне қызығушылығын арттыру, оқушыларды алғырлыққа, шапшандыққа тәрбиелеу және «Білімнің басы- бейнет, соңы -зейнет» екендігін оқушылардың санасында бекіту

Сабақта қолданылатын көрнекіліктер: интербелсенді тақта, оқулық, кеспе қағаздар, формула жазылған карточка, мақалдар жазылған есеп карточкасы.

Сабақтың әдіс-тәсілдері : көрнекіліктерді қолдану. Әңгімелеу, баяндау.
Сабақтың типі: жаңа сабақ
Сабақ барысы:

І. Ұйымдастыру. Сынып оқушыларының қатысымы. Оқушыларды топқа бөлу, зейінін шоғырландыру. Сабаққа дайындығын тексеру.

«Жұлдыздар» тобы

«Білгірлер» тобы

ІІ. Үй тапсырмасын тексеру . . Негізгі тригонометриялық тепе-теңдіктердің формулаларын сұрау.

ІІІ. Жаңа сабақ. Жаңа сабақты бастар алдында әр оқушының партасына формула жазылған мына карточканы тарқатамын; онда өткен тақырыптың да формулалары бар . Сонымен жаңа таққырыпты бастаймын.

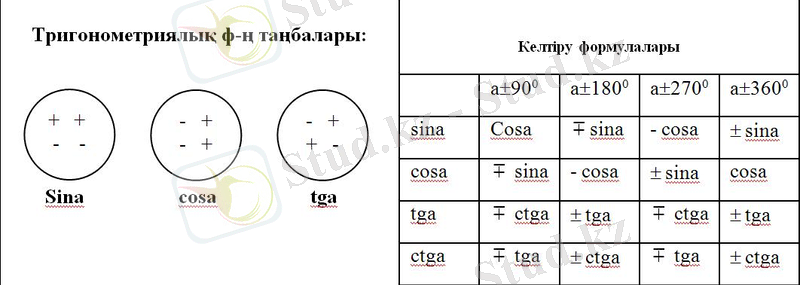
Берілген тақырыпты игере отырып, сүйір бұрыштың

тригонометриялық функциясының әрбір бұрышындағы синустың, косинустың, тангенстің, котангенстің келтіру формулаларымен танысып, осы формулаларды тригонометриялық өрнектерді түрлендіруде және есептерді шығару кезінде қолдануды үйренесіңдер.

Тригонометриялық функциялармен байланысты көптеген есептерді шығаруда тригонометриялық функцияның кез келген бұрышын тригонометриялық функциялардың сүйір бұрышына келтірудің маңызы зор. Басқаша айтқанда, егер 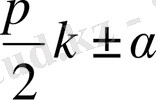(мұндағы k- кез келген бүтін сан, α - сүйір бұрыш) бұрышының функциялары берілсе, онда оларды α-бұрышына байланысты тригонометриялық функцияларға келтіру ыңғайлы. Ол үшін арнайы берілген келтіру формулалары қолданылады.

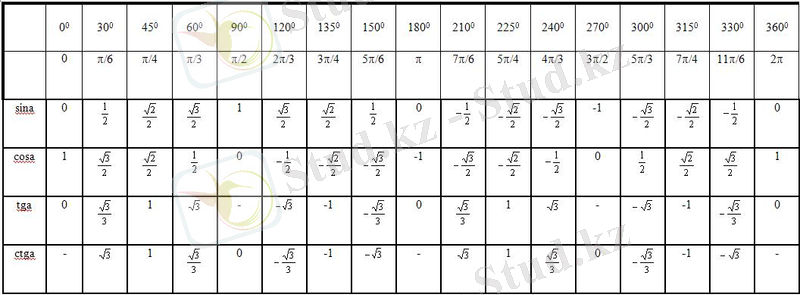
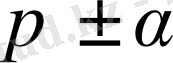
Біз тек кейбір жағдайларда ғана қолданылатын келтіру формулаларын

k = 1; 2; 3; 4 болған жағдайдағы 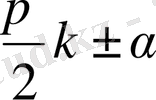өрнегін, яғни 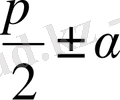; ; ; 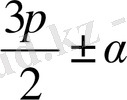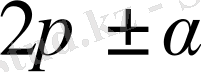бұрыштарын қарастырамыз.

Басқа бұрыштар (k-ның бүтін мәніне сәйкес қалған бұрыштар) жоғарыда көрсетілген бүтін бұрыштардың шамаларына 2π; 4 π; 6π және т. б. қосу жолымен алынады.

Алдымен синус пен косинус үшін келтіру формулаларын қарастырайық. Ал олар арқылы тангенс және котангенс үшін келтіру формулаларын оңай қорытып шығаруға болады.

ІІ ширектегі синус және косинус үшін келтіру формулаларын қорытып шығарайық. ІІ ширектегі әрбір бұрышты 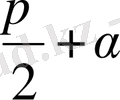түріне келтіру болады

( мұндағы α -сүйір бұрыш) . Шеңбер алайық.

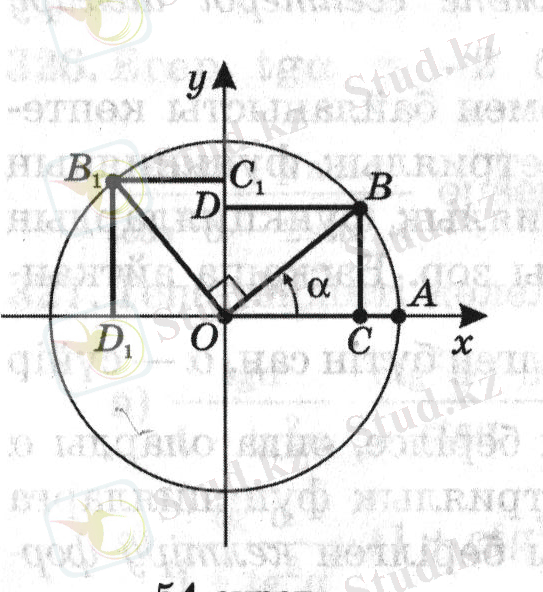
О нүктесін айналдыра шеңбердің R = OA радуысын - бұрышына бұрайық, сосын 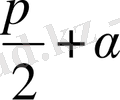бұрышына тағы да бұрамыз. Осы бұрулар кезінде ОА радиусы сәйкес ОВ және ОВ ₁ радиусына ауысады. В және В ₁ нүктелерінен координаталық осьтерге перпендикуляр түсіреміз. Нәтижесінде ОСВД және ОС ₁ В ₁ Д ₁ екі төртбұрышты аламыз. ОС ₁ В ₁ Д ₁ тік төртбұрышын оң бағытта 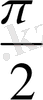бұрышына бұру арқылы шықты. Расында ВОВ ₁ = 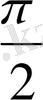болғандықтан, бұру кезінде В нүктесі В ₁ нүктесіне көшеді. Дәл осылай С нүктесі С ₁ нүктесіне, ал Д нүктесі Д ₁ нүктесіне көшеді. Содықтан В ₁ нүктесінің ординатасы ретінде В нүктесінің абсциссасын, ал В ₁ нүктесінің абсциссасы ретінде В нүктесінің ординатасын қарама-қарсы таңбамен алуға болады:

y ₁ = x және x ₁ = -y

немес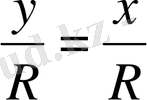е және

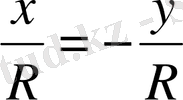
Аңықтама бойынша бұрыштың синусы ординатаның радиусқа қатынасына тең екенін білеміз, яғни

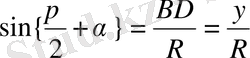, sin α =

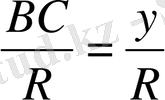
Дәл осылай

cos 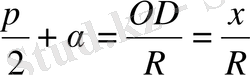, ал cos α =

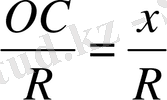
• Іс жүргізу
• Автоматтандыру, Техника
• Алғашқы әскери дайындық
• Астрономия
• Ауыл шаруашылығы
• Банк ісі
• Бизнесті бағалау
• Биология
• Бухгалтерлік іс
• Валеология
• Ветеринария
• География
• Геология, Геофизика, Геодезия
• Дін
• Ет, сүт, шарап өнімдері
• Жалпы тарих
• Жер кадастрі, Жылжымайтын мүлік
• Журналистика
• Информатика
• Кеден ісі
• Маркетинг
• Математика, Геометрия
• Медицина
• Мемлекеттік басқару
• Менеджмент
• Мұнай, Газ
• Мұрағат ісі
• Мәдениеттану
• ОБЖ (Основы безопасности жизнедеятельности)
• Педагогика
• Полиграфия
• Психология
• Салық
• Саясаттану
• Сақтандыру
• Сертификаттау, стандарттау
• Социология, Демография
• Спорт
• Статистика
• Тілтану, Филология
• Тарихи тұлғалар
• Тау-кен ісі
• Транспорт
• Туризм
• Физика
• Философия
• Халықаралық қатынастар
• Химия
• Экология, Қоршаған ортаны қорғау
• Экономика
• Экономикалық география
• Электротехника
• Қазақстан тарихы
• Қаржы
• Құрылыс
• Құқық, Криминалистика
• Әдебиет
• Өнер, музыка
• Өнеркәсіп, Өндіріс