Тригонометриялық функциялардың көбейтіндісін қосындыға және айырмаға түрлендіру формулалары


Сабақтың тақырыбы : Тригонометриялық функциялардың көбейтіндісін қосындысы немесе айрымға түрлендіру формулалары.
Сабақтың мақсаты :
Білімділік : Тригонометриялық функциялардың көбейтіндісін қосындысы немесе айрымға түрлендіру формулаларын қолданып, қиындығы әртүрлі есептер шығару;
Дамытушылық :Қиындығы әртүрлі есептер шығару кезінде алған теориялық білімін дағдысын қалыптастыру; Тәрбиелік мақсаты : Оқушыларды пәнге қызығушылығын арттырып, өз бетінше еңбек етуге, ізденуге баули отыра, ой-өрісін кеңейтіп, жауапкершілікті сезінуге, адамгершілікке баулу.
Сабақтың көрнекілігі : Интерактивтік тақтадағы биоинтернет картасы, үш деңгейлік - төменгі, аралық және жоғары (ТКШ, АКШ, ЖКШ) жаттықтырғыштар, тірек сызба .
Сабақтың әдісі : Оқу әрекетінің жинақтау әдісі «ОӘЖӘ»
Сабақтың түрі : Практикалық сабақ.
Сабақтың өту барысы:
І. Ұйымдастыру кезеңі
Ең алдымен сергіту сәтін жүргізейік.
1) Қайталау сұрақтары:
Негізгі тригонометриялық функциялар қалай аталады?
Тригонометриялық функцияның негізгі қасиеттері қандай?
2)
жылдамдыққа тексеру:
Кез келген қарапайым тригонометриялық өрнектердің мәнін қатесіз тез айту .
Өрнектің мәнін тап:
sin 45˚ + sin45˚ =
sin 45˚ - sin45˚ =
sin 45˚ * sin45˚ =
sin 30˚ * sin60˚ =
ІІ.
 ,
β, γ
топтарына бөлу үшін есептер шығару.
,
β, γ
топтарына бөлу үшін есептер шығару.
Жаттықтырғыш . ТКШ.
Жаттықтырғыш . АКШ
Жаттықтырғыш . ЖКШ
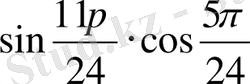

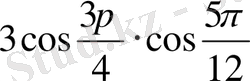

ТКШ 1. Көбейтіндіні қосындыға түрлендір:
cos( x+
 ) cos (x-
) cos (x-
 ) =
) =
 (
cos( x+
(
cos( x+
 +x-
+x-
 ) +
cos( x+
) +
cos( x+
 -x+
-x+
 ) ) =
) ) =
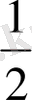 (
cos2x+cos2
(
cos2x+cos2
 )
)
Жауабы:
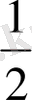 (
cos 2x+cos2
(
cos 2x+cos2
 )
)
АКШ 1.
Егер sin
 sinβ
=
sinβ
=
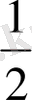 және
және
 -β=
-β=
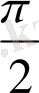 болса, онда cos(
болса, онда cos(
 +β) неге тең?
+β) неге тең?
Шешуі:
sin
 sinβ=
sinβ=
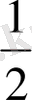 ( cos(
( cos(
 -β) -cos(
-β) -cos(
 +β) ) формуласын қолданамыз:
+β) ) формуласын қолданамыз:
=
( cos
-cos(
+β) )
:
= 0-cos(
+β)
1=0- cos(
+β)
1=- cos(
+β), cos(
+β) = -1
Жауабы: -1
ЖКШ 1. Көбейтіндіні қосындыға түрлендір:
sin
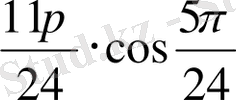 =
=
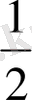 (
sin(
(
sin(
 ) +sin(
) +sin(
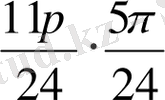 ) ) =
) ) =
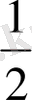 (
sin
(
sin
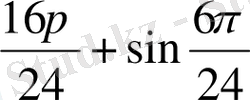 ) =
) =
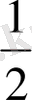 (
sin
(
sin
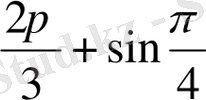 ) =
) =
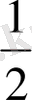 (
(
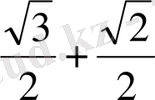 ) =
) =
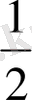
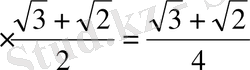
Жауабы:
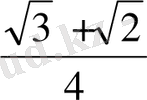
Оқушылар дәптер алмасып, есептерін тақтадағы жауаппен тексереді.
ТКШ-ны дұрыс шығарған оқушыларға -қызыл жетон, АКШ-ны дұрыс шығарғандарға -көк жетон, ал ЖКШ -ны дұрыс шығарғандарға -жасыл жетон беріледі және әрқайсысын санап, нәтижені 63% арқылы көрсетеміз.
3 есепті дұрыс шығарған оқушылар
 тобына, 2 есепті дұрыс шығарған оқушылар β тобына, ал 1 есепті дұрыс шығарған оқушыларды γ тобына отырғызамыз,
ООМ
(отырғызу орындарының матрицасын
)
сызамыз.
тобына, 2 есепті дұрыс шығарған оқушылар β тобына, ал 1 есепті дұрыс шығарған оқушыларды γ тобына отырғызамыз,
ООМ
(отырғызу орындарының матрицасын
)
сызамыз.
А Б В Г Д Е
тобынан сарапшылар шығып үш есептің шығарылуын түсіндіріп береді(тақырып сызба түрінде беріледі) және ООМ арқылы жұмыс жүргізіледі. Түсіндірме жұмыстары біткен соң, келесі этапқа көшеміз.
ІІІ Есептер шығару: ТКШ 2, АКШ 2, ЖКШ 2.
Оқушыларға жеке тапсырмалар беріледі, тірек сызбаны пайдаланып тапсырманы орындайды.
ТКШ 2.
sin(х+
 )
)

Жауабы :
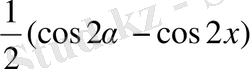
АКШ 2.
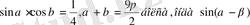 неге тең?
неге тең?
формуласын қолданамыз:
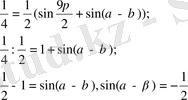
Жауабы:-
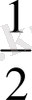
ЖКШ 2.
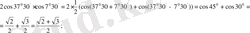 Жауабы:
Жауабы:
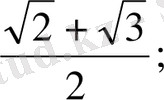
Уақыт:
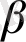 және
және
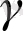 топтарына 5+30'. Уақыт біткен соң тексеріледі, нәтиже жазылады, жетон беріледі. Әр топтан оқушылар орын ауыстырады.
топтарына 5+30'. Уақыт біткен соң тексеріледі, нәтиже жазылады, жетон беріледі. Әр топтан оқушылар орын ауыстырады.
 тобының 3 сарапшысы ООМ бойынш жұмыс жүргізеді. Он «+» алып, келесі этапқа өтеміз.
тобының 3 сарапшысы ООМ бойынш жұмыс жүргізеді. Он «+» алып, келесі этапқа өтеміз.
VI Есептер шығару: ТКШ 3, АКШ 3, ЖКШ 3.
ТКШ 3.
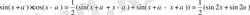
Жауабы:
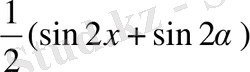
АКШ 3
.
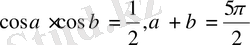 болса, онда cos(
болса, онда cos(
 -β) - неге тең?
-β) - неге тең?
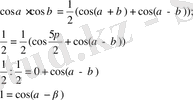
Жауабы: 1
ЖКШ 3.
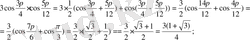
Жауабы:
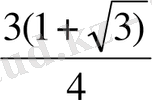
Уақыт: β және γ ға 5+30

Тексеріледі, жетон беріледі, нәтижесін жазамыз. Шығарған есептеріне қарай орын ауыстырылады.
V. Сабақты қорытындылау. Бағалау.
Сабаққа белсене қатысқан оқушыларды бағалау:
 тобының оқушыларына «5», β тобының оқушыларына «4» бағасы ал γ тобының оқушыларына «3» қойылады.
тобының оқушыларына «5», β тобының оқушыларына «4» бағасы ал γ тобының оқушыларына «3» қойылады.
VIІI. Үйге тапсырма. Үйге тапсырма оқулықтың 124-бетінде №443(1, 2), №444(1, 2) .
«Тригонометриялық функциялардың көбейтіндісін қосындысы немесе айрымға түрлендіру формулалары» тақырыбына тірек сызба.

- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz