Математика сабағында қазақтың ұлттық шежіресін қолдану

Скачать

МАТЕМАТИКА САБАҒЫНДА ҚАЗАҚТЫҢ ҰЛТТЫҚ ШЕЖІРЕСІН ҚОЛДАНУ.

Башарова Дина Қойшыбайқызы.

№51 М. Қаратаев атындағы орта мектебі.

Қандай ғылым болмасын онда қанша

математика болса, соншама шындық болады.

И. Кант.

Елбасымыз Н. Ә. Назарбаев өзінің Қазақстан халқына арнаған Жолдауында

«Бізге экономиак мен қоғамдық жаңару қажеттіліктеріне сәйкес келетін жаңа білім беру жүйесі қажет» - деп қазіргі білім саласына артылатын салмақты көрсетіп берді.

Сондықтан әрбір пән мұғалімнің алдында тұрған негізгі міндеттерінің бастысы заман талабына сай оқытудың жаңа технологиясын қолдана отырып, қоғамдық өзгерістерге бейім, өздігінен дами алатын, өзін-өзі тәрбиелейтін жеке тұлғаны қалыптастыру болмақ.

Осындай талапқа сай қызмет істеу үшін ең алдымен мұғалімге өзінің теориялық және әдістемелік білімін ұдайы жаңартып, толықтырып, үздіксіз ізденіп жүру қажет. Сонда ғана мұғалім өз жұмының нәтижесін көре алады.

Мұғалім шеберлігінің негізгі көрсеткіштерінің бірі - әдістеме саласындағы ғылыми жаңалықтар мен озық тәжірибені жетік игеру. Оларды өзінің күнделікті сабағында тиімді пайдалана білсе, мұғалімнің шығармашылық жұмысы ілгерілеп дамып отырады.

Оқушының математикадан білімін көтерудің ең басты шарты - оның пәнге деген қызығушылығын ояту және арттыру. Пәнге деген қызығушылық болса ғана, бала оған көңіл қойып, тыңдап, зейін қойып үйрене бастайды. Сонда ғана оның білім үйренуге деген белсенділігі артады.

Оқушылардың пәнге деген қызығушылығын туғызудың жолдарының көзі қазақ халқының тәрбиелік және танымдық мәні бар, баға жетпес асыл қазынасы, тарихи - мәдени мұраларында жатыр. Соның бірі - Қазақтың ұлттық шежіресі.

«Адам ата - анадан туғанда есті болмайды: естіп, көріп, ұстап, біліп оны ескерсе, дүниедегі алыс-жақын мен жақсы-жаманды білгені мен көргені көп болған адам білімді болады» - дейді Абай Құнанбаев. [1]

Абайдың бұл сөзі ұлттық шежіреге толық қатысты айтылған.

Ұлттық шежіре ата-бабамыздан бізге жеткен, өткен мен бүгінгіні, алыс пен жақынды байланыстыратын баға жетпес байлығымыз.

Математика сабағында оқушылар өздерінің ата-тегін, яғни жеті атасын білумен қатар сандардың шығу тарихы мен шежірені байланыстыра үйретуді жоспарладым.

Мақсатым:

• Ғылыми - техникалық жетістіктерді халқымыздың ғасырлар бойы қалыптасқан ұлттық дәстүрмен ұштастыра білетін қабілетті, ұлтжанды шәкірттер даярлау.
• Оқушыларды ғылыми негізде шығармашылық жұмыстарға талпындыру, өзіндік ізденіспен, тапқырлыққа үйрету.
• Оқушыларға өзінің жеті атасын білуді үйретуде сандар мен туыстық шежірелерді сәйкес қоя білуге және де пәнге қызығушылығын арттыру.
• Оқушылардың ой-өрісін кеңейту, өз халқының ұлттық мәдени бай мұраларын білуге және қастерлеуге тәрбиелеу.

Математика сабағында ұлттық мәдени мұраларды дамыта оқыту технологиясын пайдалану оқушылардың логикалық ойлау, өз бетімен жұмыс істей алу дағдыларының дамуына ықпалын тигізеді.

Қандайда бір жаңа ұғымды қалыптастыру, яғни ғылымды игерту сол халықтың ұлттық ерекшелігімен тығыз байланыста жүргізілсе оны қабылдау нәтижелі болады.

Біз - қазақ атаны, ананы пір тұтқан халықпыз.

Сондықтан біз тегімізді - атадан, тілімізді - анадан сұраған халықпыз

Қорқыт ата кітабында:

«Атасыз ұл - ақылға жарымас,

Анасыз қыз жасауға жарымас» - деп тегіннен - тегін айтпаған.

Қазақ « Жеті атасын білмеген - жетімдіктің белгісі»,

«Жеті атасын білген - жеті рудың қамын жейді» деп санайды.

Тарихи сыры да көп айтылатын мұңы да көп түркі текті халықтардың ішіндегі іргелісінің бірі, бір де болса бірегей - қазақ халқы.

«Қазақ - түрік емес, қазақсыз - түрік, түрік емес» - деген ежелгі мәтелдерден ер қазақтың ерен мінезін, абзал қасиетін, асқақ көңілін, ата тарихына деген сүйіспеншілігін аңғарамыз[2]

Жалпы ұлтымыздың дарындылығын Академик О. Жәутіков : «Қазақ халқы - дарынды халық. Біз математика мен механикадан дүниежүзі ғалымдарының назарын өзімізге аударуымыз керек» - деп бағалауы болашаққа деген сенімімізді арттырады [3]

Қазақ туыстық жақындықты былай бөледі:

1-кесте

[4]

Адамзат тарихында ежелде қалыптасқан ғылым-математика. Математиканың алғашқы бесігі Мысыр елі, ал екінші бесігі Үнді елі болған. Дүние жүзінде қолданылып жүрген цифрлардың түп төркіні Индиядан шыққан.

Сандардың шығу тарихы 2-кесте

[5]

1. Натурал сандар: N = {1. 2. 3 . . . , n…}

2. Бүтін сандар: Z = {0. ±1, $\mathbf{\pm}$ $\mathbf{\pm}$ ± 2, $\mathbf{\pm}$ $\mathbf{\pm}$ ± 3 . . . }

3. Рационал сандар: Q = { $\frac{m}{n}$ $\frac{\mathbf{m}}{\mathbf{n}}$ } мұндағы m € Z

n € N

4. Нақты сандар. R = {- ∞; +∞}

$\mathbf{I}^{\mathbf{2}}$ 5. Жорамал сандар: $i^{2}$ = - 1, I- жорамал бірлік.

6. Комплекс сандар: а+bi, мұндағы а-комплекс санның нақты бөлігі.

bi - жорамал бөлігі.

1) Сан ұғымы адамзат тарихының терең түкпірінен орын алады.

Нәрселерді санау нәтижесінде 1, 2, 3 . . . қалыптасып, яғни заттар тобына белгілі бір сан

сәйкес қойылды.

Жоқ нәрсеге (затқа) ноль саны сәйкес қойылды. Сонымен теріс емес бүтін сандар қалыптасты. 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

Теріс емес бүтін сандар жиынына қосу, көбейту амалдары үнемі орындалады, бірақ

азайту, бөлу амалдары әруақытта орындала бермейді. Мұның өзі сан ұғымын кеңейту керектігін талап етеді.

2) Енді әрбір теріс емес бүтін санға қарама-қарсы сандарды сәйкес қойсақ, барлық бүтін

сандар жиынын аламыз. Бұл жиында қосу, көбейту, азайту амалдарын орындауға

болады, бірақ бөлу амалы орындала бермейді, сондықтан тағыда сан ұғымын кеңейту

қажеттігі туады.

3) Рационал сандар жиынында қосу, көбейту, азайту, нольден басқа санға бөлу амалдары

орындалады, яғни бұл сандар адамзаттың күнделікті тұрмыс-тіршілігі үшін толық

жеткілікті. Алайда, ғылым мен техниканың дамуына байланысты, қарапайым

теңдеулерді шешу үшін рационал сандардың жеткіліксіз екендігі байқалды.

Квадраты 2-ге тең болатын санды иррационал сан дейді.

4) Рационал және иррационал сандар жиынын біріктіріп, нақты сандар жиынын аламыз.

Ғылым мен техниканың даму қарқыны нақты сандардың да жеткіліксіз болатындығын

көрсетті.

$\ \ \$ 5. Квадраты -1-ге тең болатын сан бар, ол «i» деп белгіленеді. Яғни $\ \ \$ $i^{2}$ $i^{2}$ = - 1.

I- жорамал бірлік.

6. а+bi түріндегі санның нақты бөлігі, ал «bi» жорамал бөлігі деп аталады.

Жорамал сандар мен комплекс сандар мектеп қабырғасында арнайы тақырып болып

өтілмейді. Бұл сандар жоғарғы оқу орындарында қолданылады.

1-схема

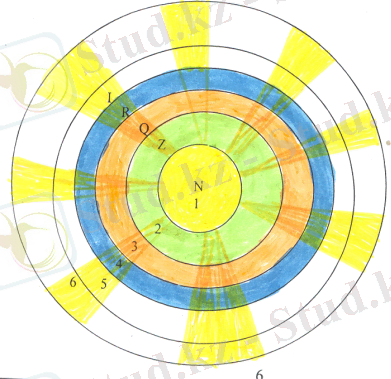
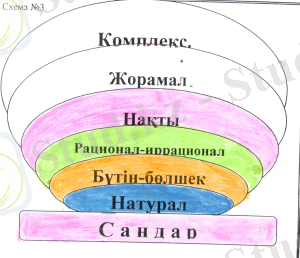N- натурал сандар

Z- бүтін сандар

Q- рационал сандар

P- нақты сандар

• Іс жүргізу
• Автоматтандыру, Техника
• Алғашқы әскери дайындық
• Астрономия
• Ауыл шаруашылығы
• Банк ісі
• Бизнесті бағалау
• Биология
• Бухгалтерлік іс
• Валеология
• Ветеринария
• География
• Геология, Геофизика, Геодезия
• Дін
• Ет, сүт, шарап өнімдері
• Жалпы тарих
• Жер кадастрі, Жылжымайтын мүлік
• Журналистика
• Информатика
• Кеден ісі
• Маркетинг
• Математика, Геометрия
• Медицина
• Мемлекеттік басқару
• Менеджмент
• Мұнай, Газ
• Мұрағат ісі
• Мәдениеттану
• ОБЖ (Основы безопасности жизнедеятельности)
• Педагогика
• Полиграфия
• Психология
• Салық
• Саясаттану
• Сақтандыру
• Сертификаттау, стандарттау
• Социология, Демография
• Спорт
• Статистика
• Тілтану, Филология
• Тарихи тұлғалар
• Тау-кен ісі
• Транспорт
• Туризм
• Физика
• Философия
• Халықаралық қатынастар
• Химия
• Экология, Қоршаған ортаны қорғау
• Экономика
• Экономикалық география
• Электротехника
• Қазақстан тарихы
• Қаржы
• Құрылыс
• Құқық, Криминалистика
• Әдебиет
• Өнер, музыка
• Өнеркәсіп, Өндіріс