Квадрат теңдеуге келтірілетін теңдеулер жайлы ақпарат. ( 8-сынып )

8-сынып, алгебра

Күні: ____________

Сабақтың тақырыбы: Квадрат теңдеуге келтірілетін теңдеулер

Сабақтың мақсаты:

Білімділік: Бұл тақырыпты игере отырып,биквадрат теңдеу ұғымымен, квадрат теңдеуге келтірілген басқа теңдеулер түрімен таныстыру

Дамытушылық: Биквадрат теңдеулерді шешу алгоритмін білу

Тәрбиелік: Оқуға, саналы сезімге, жауапкершілікке, өз бетінше еңбектенуге
тәрбиелеу

Сабақтың түрі: Жаңа сабақ

Әдіс-тәсіл, құралдары: Сұрақ-жауап, тест тапсырмалары,білімді
жүйелеу,интерактивтік тақта

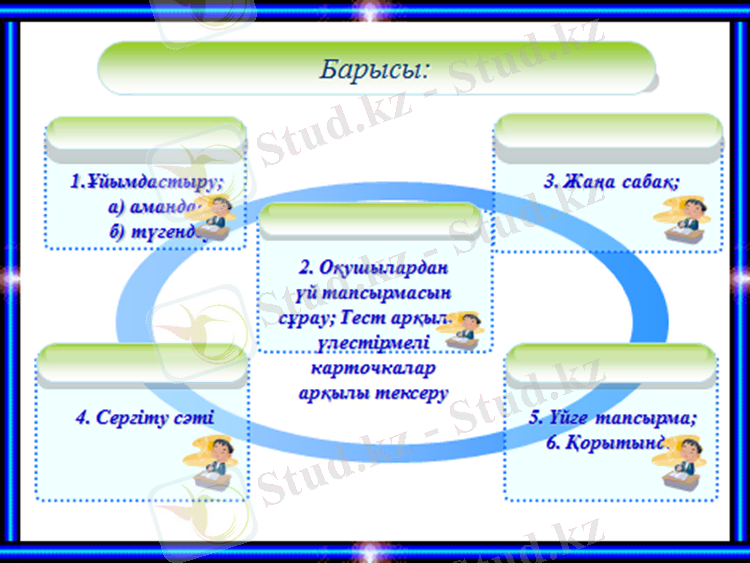
Сабақтың барысы:

І Ұйымдастыру бөлімі
Сәлемдесу
Оқушыларды түгендеу

ІІ Үй жұмысын тексеру
1.Есептердің шығарылуын тексеру
2.Ой қозғау Қайталау-білім айнасы сұрақ-жауап
Квадрат теңдеудің түрлерін сұрау

ІІ Жаңа сабақ: Квадрат теңдеуге келтірілетін теңдеулер
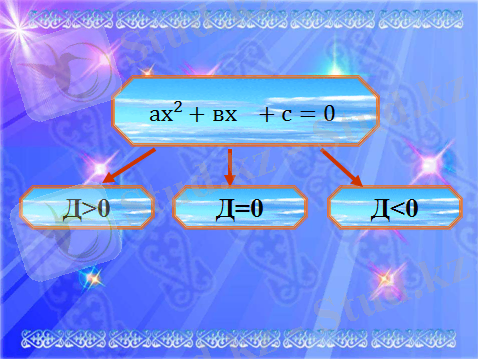
теория ах4+вх2+с=0, мұндағы а!=0 түрінде берілген теңдеу биквадрат теңдеу деп аталады.
Мысалы: х4+8х2-9=0 теңдеуін шешейік х2=у у2+8у-9=0 дискриминантын тауып, түбірлерін іздейміз у=-9 у=1 шыққан түбірді х2=у апарып қоямыз, х2=-9 теңдеуінің түбірі болмайды х2=1 теңдеуінен х=-1 х=1 екі түбірі шығады
Теңдеулерді шешудің мұндай әдісі жаңа айнымалы еңгізу әдісі деп аталады.
Теңдеулерді шешудің жаңа айнымалы еңгізу әдісімен шешу алгоритм құру (оқушылармен біріге отырып)
* Теңдеудегі қандайда бір өрнекті жаңа айнымалы арқылы белгілейміз
* Берілген теңдеудегі өрнектің орнына жаңа айнымалыны енгізіп, жаңа айнымалыға байланысты квадрат теңдеу аламыз
* Шыққан квадрат теңдеуді шешеміз
* Алмастыру арқылы алғашқы айнымалының мәнін табамыз
* Табылған түбірлерге тексеру жүргізіп, берілген теңдеудің түбірлерін аықтаймыз
Тақтамен жұмыс мысалды біріге отырып талдаух2+2х-6х2+2х=-5

ІІІ Сабақты бекіту:

№189-1,3 ) №190-2,4) №191-1,3) есептерді тақтада орындау

IV.Сабақты бекіту.Деңгейлік тапсырма

V.Сергіту сәті. Белгісіз санды табу ( таблицаны толтыру)
VI.Үйге тапсырма беру §10 оқу №189-2,4) , №190-1,3), №192-2,4)
VII.Бағалау
254005651500

-5715127000

-5715508000

№

154305-317500

Рисунок 1Деңгейлік тапсырма
26606575120500Іздеген табар,оқыған озар

4749803302000

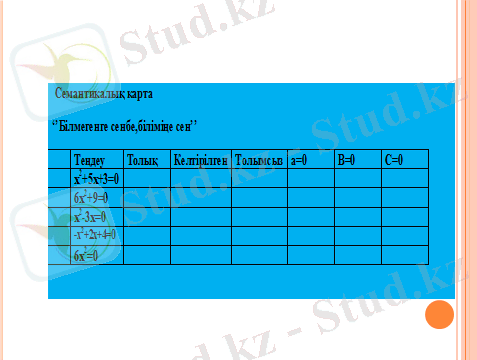
Семантикалық карта
`'Білмегенге сенбе,біліміңе сен''
№
Теңдеу
Толық
Келтірілген
Толымсыз
а=0
В=0
С=0
1
х2+5х+3=0

2
6х2+9=0

3
х2-3х=0

4
-х2+2х+4=0

5
6х2=0

4749804191000