Келтіру формулаларына есептер

1. Ұйымдастыру

(3мин)

1. Оқушылармен амандасу;
2. Оқушылардың көңілдерін сабаққа аудару
3. Математикалық сиқырды орындату

Мұғаліммен амандасады.

Көңілдерін сабаққа аударады.

Математикалық сиқырды орындайды.

2. Үй тапсырмасын

тексеру (3мин)

Келтіру формулаларын қолдана білуге есеп.

№ 408 (3)

$\alpha = \frac{5\pi}{6} = > sin\frac{5\pi}{6} = sin(\pi - \ \frac{\pi}{6}) = sin\frac{\pi}{6} = \frac{1}{2}\$

$\cos\frac{5\pi}{6}\ = cos(\pi - \frac{\pi}{6}) = - cos\frac{\pi}{6} = - \frac{\sqrt{3}}{2}\$ $\cos\frac{5\pi}{6}\ = cos(\pi - \frac{\pi}{6}) = - cos\frac{\pi}{6} = - \frac{\sqrt{3}}{2}\$

$tg\frac{5\pi}{6} = tg(\pi - \ \frac{\pi}{6}) = - tg\frac{\pi}{6} = - \frac{\sqrt{3}}{3}$ $tg\frac{5\pi}{6} = tg(\pi - \ \frac{\pi}{6}) = - tg\frac{\pi}{6} = - \frac{\sqrt{3}}{3}$

c $tg\frac{5\pi}{6} = ctg(\pi - \ \frac{\pi}{6}) = - ctg\frac{\pi}{6} = - \sqrt{3}$ $tg\frac{5\pi}{6} = ctg(\pi - \ \frac{\pi}{6}) = - ctg\frac{\pi}{6} = - \sqrt{3}$

Топ президенттері конверт суырады.

1) әр топ (1, 2, 3) өздері білетін, жаттаған

формулаларын жазады.

2) Топ жұмыстарын өзара ауыстырып интерактивті

тақтада көрсетілген

дұрыс жауап пен тексереді. Топтың

өздеріне қайтарып, топ президенті

бағалау парағының, үй тапсырмасын

тексеру бөліміне ұпай түсіреді.

3. Ой қозғау(Формулаларға талдау. )

(7мин)

Келтіру формулаларын қалай есте сақтап, шапшаң жаттауга болады ? (Осы сұраққа талдау жасау. )

1-оқушы 2-оқушы

$\frac{\pi}{2} + \alpha; \ \ \ \ \frac{\pi}{2} - \alpha; \$ $\pi + \alpha; \ \ \ \pi - \alpha\$

$\frac{\pi}{2} + \alpha; \ \ \ \ \frac{\pi}{2} - \alpha; \$ $\frac{3\pi}{2} + \alpha; \ \ \ \ \frac{3\pi}{2} - \alpha; \$ $2\pi + \alpha; \ \ \ 2\pi - \alpha\$

$\frac{3\pi}{2} + \alpha; \ \ \ \ \frac{3\pi}{2} - \alpha; \$

$\pi + \alpha; \ \ \ \pi - \alpha\$

$2\pi + \alpha; \ \ \ 2\pi - \alpha\$

Оқушылардың талдауы:

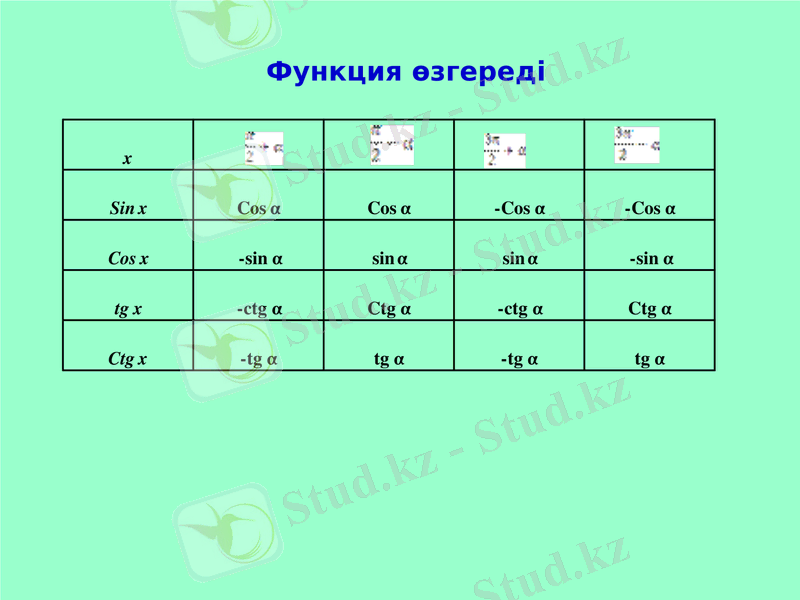
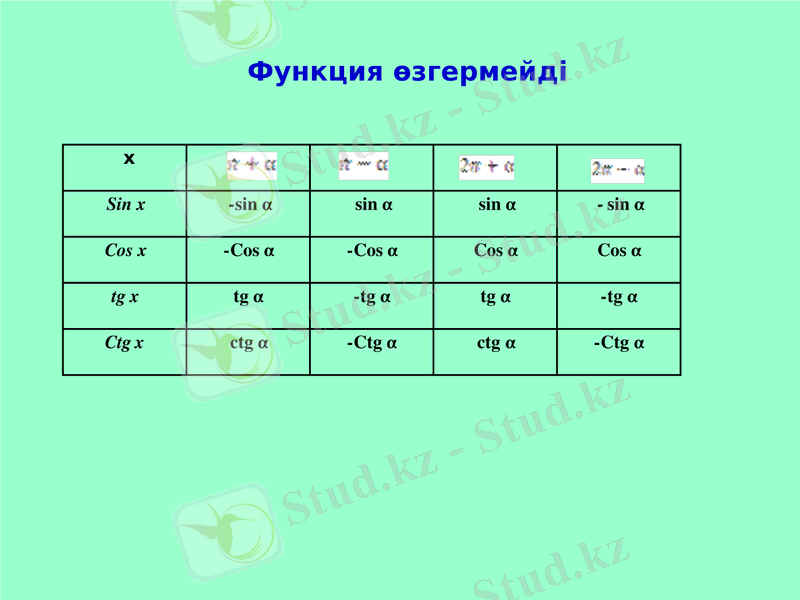
4. Оқулықпен жұмыс

(15мин)

Келтіру формулаларын қолдануға есептер; № 412. Деңгейлік тапсырмалар.

1. 3sin⁡π2+4cos2π3+6sin13π6=43\sin{\frac{\pi}{2} + 4cos\frac{2\pi}{3} + 6sin\frac{13\pi}{6}} = 4
2. 1800180^{0}2700270^{0}1800180^{0}

$3\sin{\frac{\pi}{2} + 4cos\frac{2\pi}{3} + 6sin\frac{13\pi}{6}} = 4$ 2tg $180^{0}$ -0, 5 sin(- $270^{0}$ ) +0, 5 cos $180^{0}$ = -1№ 419

2. sin⁡7π4•cos7π6•tg5π3•ctg4π3=−64\sin\frac{7\pi}{4} \bullet cos\frac{7\pi}{6} \bullet tg\frac{5\pi}{3} \bullet ctg\frac{4\pi}{3} = - \frac{\sqrt{6}}{4}

$\sin\frac{7\pi}{4} \bullet cos\frac{7\pi}{6} \bullet tg\frac{5\pi}{3} \bullet ctg\frac{4\pi}{3} = - \frac{\sqrt{6}}{4}$ $\cos{( - 7, 9\pi) \bullet tg( - 1, 1\pi) - \sin{5, 6\pi \bullet ctg\ 4, 4\pi = 0}}$

5. Ой толғаныс (топшама)

(10мин)

Топшамалар. Ықшамдаңдар

1. cos⁡2(3π2−α) •ctg2(2π−α) \cos^{2}\left( \frac{3\pi}{2} - \alpha \right) \bullet {ctg}^{2}(2\pi - \alpha)
2. sin⁡2(π+α) •tg2(π2+α) \sin^{2}(\pi + \alpha) \bullet {tg}^{2}\left( \frac{\pi}{2} + \alpha \right)

1. sin⁡(α−3π2) •tg(α−2π) \sin\left( \alpha - \frac{3\pi}{2} \right) \bullet tg(\alpha - 2\pi)
2. cos⁡2(α−3π2) +sin⁡2(−α) \cos^{2}\left( \alpha - \frac{3\pi}{2} \right) + \sin^{2}( - \alpha)

$\cos^{2}\left( \frac{3\pi}{2} - \alpha \right) \bullet {ctg}^{2}(2\pi - \alpha)$ $\sin^{2}(\pi + \alpha) \bullet {tg}^{2}\left( \frac{\pi}{2} + \alpha \right)$ $\sin\left( \alpha - \frac{3\pi}{2} \right) \bullet tg(\alpha - 2\pi)$ $\cos^{2}\left( \alpha - \frac{3\pi}{2} \right) + \sin^{2}( - \alpha)$