Stud.kz
Сабақ жоспары :: Математика

Геометрия, "хан тәңіріне саяхат", 8-сынып

Күнделік сабақ жоспары

Мерзімі __15. 02 ___ Геометрия Сынып 8 «А»

Сабақтың тақырыбы: «Хан Тәңіріне» саяхат .

Сабақтың мақсаттары:

1. «Төртбұрыштар», «Үшбұрыштардың және төртбұрыштардың аудандары», «Үшбұрыштағы метрикалық қатыстар» тараулары бойынша алған білімдерін есте қайта жаңғырту
2. Логикалық ойлау, есте сақтау, алған білімдерін есептеуде, ауызша есептеуде қолдана білу қабілеттерін, пәнге деген қызығушылығын дамыту
3. Ұлттық сана сезімі оянған, рухани ойлау дәрежесі биік, еңбекқор, іскер, білімді және білімін пайдалана білетін, бүгінгіні түсінетін, кешегіні білетін, алдына мақсат қойып, оған жетер жол таба білетін ұрпақ тәрбиелеу, оқушылардың патроиоттық сезімдерін қалыптастыру.

Сабақтың түрі: Саяхат сабағы

Сабақтың типі: Жаттығу және қайталау сабағы

Оқытудың әдістері: Сұрақ-жауап, деңгейлеп дамыта оқыту, ойын технологиясы элементтері.

Оқытудың формасы: Кіші топпен жұмыс

Пәнаралық байланыс: География, тарих

Сабақтың көрнекілігі: 1. Презентация-слайд 2. Жетондар 3. Үлестірмелі материалдар

Сабақтың барысы:

І. Ұйымдастыру кезеңі

а) Сәлемдесу;

ә) Сабаққа келмеген оқушыларды анықтау;

б) Оқушылардың сабаққа дайындығын тексеру;

в) Оқушыларды саяхат жоспарымен, ережелерімен таныстыру;

ІІ. Саяхат жоспары

Хан Тәңірі шыңы Қазақстанның ең биік нүктесі, Орталық Тянь-Шаньның ең әдемі шыңдарына жатады. Үшкір пирамидаға ұқсас мәрмәр шың барлық жерден көрінеді. Бұл шыңға байланысты неше түрлі аңыздар бар, оның басқаша аты Тәңіртау немесе Қантау, соңғы атаудың себебі кешкі күн батқан уақытта шыңның түсі қызғылт түске боялады. Жетімыңдық шыңдардың ең солтүстікте орналасқаны осы Хан Тәңірі шыңы.
Хан Тәңірі шыңына шығу тым қиын, сондықтан альпинистер мен эксремалды туризм ұнататындарға өте қызық. Қазақстанға шыңның солтүстік жағы қарайды. «Хан Тәңірінің солтүстік жарына» шығу көптеген альпинистердің арманы болып саналады.
Хантәңірі шыңы теңіз деңгейінен 7010 метр биікте тұр. Шыңның оңтүстік бөлігі Қытайға, батысы Қырғызстанға қараса, солтүстіктегі бөлігі біздің елге тиесілі.
Хантәңірі шыңы жайлы деректер ертедегі жиһангездердің жазбаларында кездеседі. Дегенмен ғылыми тұрғыдағы алғашқы мәліметтер ХІХ ғасырда орыстың әйгілі саяхатшысы Петр Семенов-Тянь-Шанскийдің еңбегінде тіркелді.

  • Саяхатқа екі топ шығады.
  • «Алғырлар» тобының лидері Айгерім.

«Тапқырлар» тобының лидері Арман.

  • Саяхатшылар өз араларынан жолсерік таңдайды.
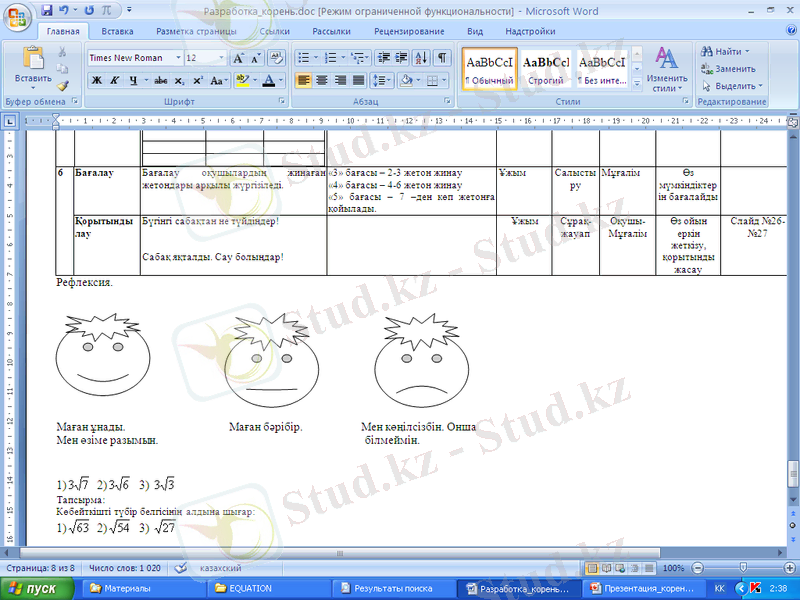
  • Жолсерік есептеулерді дұрыс орындаған оқушыларға жетондар таратып отырады, жетон бағасын «Жол парағына» қойып отырасыңдар

Жол парағы

Аты-жөні .

І бөлім

☺😐☹

Менің сабақтағы жұмысымның мақсаты . . .

□ Топта жұмыс жасауға, қарым-қатынас жасауға үйрену

□ Төртбұрыштардың түрлерін ажырата білуге, қасиеттерін анықтай білуге үйрену

□ Төртбұрыштар мен үшбұрыштардың аудан формулаларын есеп шығаруда қолдана білуге үйрену

□ Тригонометриялық тепе-теңдіктерді, тікбұрышты үшбұрыштың сүйір бұрыштарының sin, cos, tg, ctg-ының градустық өлшемдерін қолданып есепті жақсы шығаруға үйрену

Аялдамалар
Жолсерік бағасы
Өз - өзі бағалау
Мұғалім бағасы
Жалпы баға
Аялдамалар: 1. Чистопол селосы
Жолсерік бағасы:
Өз - өзі бағалау:
Мұғалім бағасы:
Жалпы баға:
Аялдамалар: 2. Көкшетау қаласы
Жолсерік бағасы:
Өз - өзі бағалау:
Мұғалім бағасы:
Жалпы баға:
Аялдамалар: 3. Астана қаласы
Жолсерік бағасы:
Өз - өзі бағалау:
Мұғалім бағасы:
Жалпы баға:
Аялдамалар: 4. Алматы қаласы
Жолсерік бағасы:
Өз - өзі бағалау:
Мұғалім бағасы:
Жалпы баға:
Аялдамалар: 5. Хан Тәңірі шыңы
Жолсерік бағасы:
Өз - өзі бағалау:
Мұғалім бағасы:
Жалпы баға:
Аялдамалар: Қорытынды баға
Жолсерік бағасы:

ІІ бөлім

Менің сабақ қорытындым:

Мен өз мақсатыма жеттім: ия жоқ (қажеттісінің астын сыз)

Мен аялдама тапсырмасын орындауда қиналдым.

Маған жалғыз, топпен жұмыс істеген ыңғайла (астын сыз)

Менің сабақты бағалауым

  • Саяхатымызды Чистопол автостанциясынан бастаймыз. Билет сатып алуға кезекке тұрыңдар.
  1. Барлық бұрыштары тік болатын параллелограмм
  2. Қарама-қарсы екі қабырғасы тең әрі параллель болатын төртбұрыш
  3. Барлық қабырғалары тең параллелограмм
  4. Барлық қабырғалары тең тіктөртбұрыш
  5. Тек екі қабырғасы ғана параллель болатын дөңес төртбұрыш
  6. Трапецияның орта сызығы . . . тең
  7. Үшбұрыштың орта сызығы . . . тең.
  8. Диагональдары перпендикуляр болатын параллелограмм
  9. Диагональдары тең әрі перпендикуляр болатын төртбұрыш
  10. Тікбұрышты үшбұрыштың үлкен қабырғасы
  11. Тікбұрышты үшбұрыштың кіші қабырғалары?
  12. Төртбұрыштың ішкі бұрыштарының қосындысы
  13. Төртбұрыштың іргелес бұрыштарының қосындысы
  14. Тікбұрышты үшбұрыштың сүйір бұрыштарының қосындысы?

Көкшетау қаласына жеткенше дейін 4, 5-5 сағат уақытымыз бар, сондықтан уақытымыз тез өтіп кетсін деп жолда тапсырмалар орындайық.

:
  1. Қарама-қарсы қабырғалары параллель
: +
: +
: +
: +
:
  1. Барлық қабырғалары тең.
:
:
: +
: +
: 3. Қарама-қарсы бұрыштары тең, іргелес бүрыштарының қосындысы180.
: +
: +
: +
: +
: 4. Барлық бұрыштары тік.
:
: +
:
: +
: 5. Диагоналдары қилысып, қилысу нүктесінде қақ бөлінеді.
: +
: +
: +
: +
: 6. Диагоналдары тең.
:
: +
:
: +
: 7. Диагоналдары өзара перпендикуляр және сәйкес бұрыштарының биссектрисасы болады.
:
:
: +
: +
  • Міне, Көкшетауға да жетіп қалдық, темір жол вокзалына барып билет алайық. Билетке кезекке тұрыңдар.
  1. Тік төртбұрыштың ауданы
  2. Қабырғасы 4 см квадраттың ауданы
  3. Тік бұрышты үшбұрыштың ауданы
  4. Параллелограммның ауданы
  5. Кез келген үшбұрыштың ауданы
  6. Трапецияның ауданы
  7. Ромбының ауданы
  8. Квадраттың ауданы
  9. Қабырғалары 3 және 5 см болатын тік төртбұрыштың ауданы
  10. Катеттері 6 және 3 см болатын тік бұрышты үшбұрыштың ауданы
  11. Үшбұрыштың орта сызығы 7 см, табаны нешеге тең?
  12. Ауданы 144см2болатын квадраттың қабырғасы
  13. Периметрі 20см болатын квадраттың ауданы
  14. Ауданы 9 см2квадраттың периметрі?

Астанаға жеткенше дейін сөзжұмбақ шешейік

Г
е
р
о
н
:
Г: п
е: а
р: р
о: а
н: л
: л
Е
л
о
г
р
а
м
м
:
Г: г
е: и
р: п
о: О
н: т
: е
н
у
з
а
:
Г: р
е: о
р: М
о: Б
н:
:
:
Г: т
е: а
р: н
о: г
н: Е
: н
с
:
Г: к
е: а
р: Т
о: е
н: т
: т
Г: ө
е: Р
р: т
о: б
н: ұ
: р
ы
ш
:
Г: п
е: И
р: ф
о: а
н: г
: о
р
: т
Г: р
е: а
р: п
о: е
н: ц
: и
Я
  1. S=p(p−a) (p−b) (p−c) \sqrt{p(p - a) (p - b) (p - c) }- кімнің формуласы?
  2. Қарама-қарсы қабырғалары қос-қостан параллель болатын төртбұрыш
  3. Тікбұрышты үшбұрыштың үлкен қабырғасы
  4. Барлық қабырғалары тең параллелограмм
  5. Тікбұрышты үшбұрыштың сүйір бұрышына қарсы жатқан катеттің іргелес жатқан катетке қатынасы
  6. Тікбұрышты үшбұрыштың кіші қабырғасы
  7. Ауданы S=ab-ға тең фигура
  8. «Гипотенузаның квадраты катеттерінің квадраттарының қосындысына тең» кімнің теоремасы?
  9. Екі қабырғасы ғана параллель болатын дөңес төртбұрыш
  • Міне, сөзжұмбақты шешіп болғанша Астанаға да жетіп қалыппыз. Енді барып Алматыға дейін билет алуға кезекке тұрайық.
  1. sin300(½)
  2. cos300(√3/2)
  3. tg300(√3/3)
  4. ctg300(√3)
  5. sin450(√2/2)
  6. cos450(√2/2)
  7. tg450(1)
  8. ctg450(1)
  9. sin600(√3/2)
  10. cos600(1/2)
  11. tg600(√3)
  12. ctg600(√3/3)
  13. тригонометрияның негізгі тепе-теңдігі
  14. tg-ті sin және cos арқылы өрнекте

Алматыға жеткенше тест тапсырмасын орындайық

І нұсқа
ІІ нұсқа
І нұсқа:
  1. Мәнін тап: 30*с𝐭𝐠𝟒𝟓𝟎\mathbf{\ с}\mathbf{tg}\mathbf{45}^{\mathbf{0}}-5*𝐭𝐠𝟒𝟓𝟎\mathbf{\ }\mathbf{tg}\mathbf{45}^{\mathbf{0}}

А. 30 Ә. 5 Б. 35 В. 25

ІІ нұсқа:
  1. Мәнін тап: 6𝐬𝐢𝐧𝟑𝟎𝟎{\mathbf{\sin}\mathbf{30}}^{\mathbf{0}}- 2с𝐭𝐠𝟒𝟓𝟎\mathbf{\ с}\mathbf{tg}\mathbf{45}^{\mathbf{0}}

А. 1 Ә. 4 Б. 8 В. 0

І нұсқа:

2. Мәнін тап: 2 𝐜𝐨𝐬 𝟔𝟎 𝟎 + 𝟐 𝐬𝐢𝐧 𝟒𝟓 𝟎 − 𝟐 {\mathbf{\cos}\mathbf{60}}^{\mathbf{0}}\mathbf{+ \ }{\mathbf{2}\mathbf{\sin}\mathbf{45}}^{\mathbf{0}}\mathbf{-}\sqrt{\mathbf{2}}

А. 2 \sqrt{2} Ә. 2 Б. 1 В. 0

ІІ нұсқа:

2. Мәнін тап: 𝟐 𝐬𝐢𝐧 𝟑𝟎 𝟎 {\mathbf{\ 2}\mathbf{\sin}\mathbf{30}}^{\mathbf{0}} + 2 с 𝐨 𝐬 𝟑𝟎 𝟎 {\mathbf{с}\mathbf{os}\mathbf{30}}^{\mathbf{0}} - 𝟑 \sqrt{\mathbf{3}}

А. 3 \sqrt{3} Ә. 1 Б. 0 В. 2

І нұсқа:

3. 𝟐 𝐬𝐢𝐧 𝟑𝟎 𝟎 {\mathbf{\ 2}\mathbf{\sin}\mathbf{30}}^{\mathbf{0}} +4 𝐜𝐨𝐬 𝟔𝟎 𝟎 {\mathbf{\cos}\mathbf{60}}^{\mathbf{0}} + 4 𝐭 𝐠 𝟒𝟓 𝟎 = ? {\mathbf{tg}\mathbf{45}}^{\mathbf{0}}\mathbf{= ?}

А. 10 Ә. 7 Б. 3 \sqrt{3} В. 2 \sqrt{2}

ІІ нұсқа:

3. 𝟒 𝐬𝐢𝐧 𝟑𝟎 𝟎 {\mathbf{\ }\mathbf{4}\mathbf{\sin}\mathbf{30}}^{\mathbf{0}} − 𝟐 𝐜𝐨𝐬 𝟔𝟎 𝟎 \mathbf{- 2}{\mathbf{\cos}\mathbf{60}}^{\mathbf{0}} + 𝟐 𝐜 𝐭 𝐠 𝟒𝟓 𝟎 = ? \mathbf{2}{\mathbf{ctg}\mathbf{45}}^{\mathbf{0}}\mathbf{= ?}

А. 4 Ә. 3 \sqrt{3} Б. 3 В. 2 \sqrt{2}

І нұсқа:

4. Ықшамда: 𝟏 − 𝐜𝐨𝐬 𝟐 𝛂 𝐬 𝐢 𝐧 𝛂 \frac{\mathbf{1 -}\mathbf{\cos}^{\mathbf{2}}\mathbf{\alpha}}{\mathbf{sin\alpha}}

А. sinα Ә. cosα Б. tgα В. ctgα

ІІ нұсқа:

4. Ықшамда: 𝟏 − 𝐬𝐢𝐧 𝟐 𝛂 𝐜𝐨𝐬 ⁡ 𝛂 \frac{\mathbf{1 -}\mathbf{\sin}^{\mathbf{2}}\mathbf{\alpha}}{\mathbf{\cos\alpha}} ;

А. ctgα Ә. tgα Б. sinα В. cosα

І нұсқа:

5. Ықшамда: 𝟏 − 𝐜𝐨𝐬 𝟐 𝛂 𝟏 − 𝐬𝐢𝐧 𝟐 𝛂 \frac{\mathbf{1 -}\mathbf{\cos}^{\mathbf{2}}\mathbf{\alpha}}{\mathbf{1 -}\mathbf{\sin}^{\mathbf{2}}\mathbf{\alpha}} ;

А. t g 2 {tg}^{2} α Ә. c t g 2 {ctg}^{2} α Б. 1 В. 0

ІІ нұсқа:

5. Ықшамда: 𝟏 − 𝐬𝐢𝐧 𝟐 𝛂 𝟏 − 𝐜𝐨𝐬 𝟐 𝛂 \frac{\mathbf{1 -}\mathbf{\sin}^{\mathbf{2}}\mathbf{\alpha}}{\mathbf{1 -}\mathbf{\cos}^{\mathbf{2}}\mathbf{\alpha}} ;

А. 1 Ә. 0 Б. t g 2 {tg}^{2} α В. c t g 2 {ctg}^{2} α


Ұқсас жұмыстар
Шыққан санды ата
Ежелгі египеттің әдебиеті мен өнері
Бір айнымалысы бар сызықтың теңдеу тақырыбына есептер шығару
Сабақтың тақырыбы. АШЫҚ САБАҚ
Қалған бұрыштарды тап
Хан батыры атағын алған батыр
Математикадан өткенді пысықтау
Қазақ батырларының жоңғарларға қарсы.отан соғысы
Жаттығу жұмысы.Сөйлемдегі сөздердің байланысын сұрақ қою арқылы
Грамматикалық тақырып
Пәндер

Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.

google play appstore

instagram tiktok

Ақпарат

Қосымша


Email: info@stud.kz



Реферат Курстық жұмыс Диплом Материал Диссертация Практика Презентация Сабақ жоспары Мақал-мәтелдер 1‑10 бет 11‑20 бет 21‑30 бет 31‑60 бет 61+ бет Негізгі Бет саны Қосымша Іздеу Ештеңе табылмады :( Соңғы қаралған жұмыстар Қаралған жұмыстар табылмады Тапсырыс Антиплагиат Қаралған жұмыстар kz