8-сынып: Ромб пен квадрат - анықтамалар, қасиеттері және есептер


А. Ромбының анықтамасын біледі.
В. Ромбының қасиеті мен белгілерін біледі, есеп шығара алады.
С. Күрделі есептер шығара алады.
Сәлемдесіп бір-біріне сәттілік тілейді.
Дайын жауабы арқылы есептерін тексереді. Өзін-өзі бағалау
Өткенді қайталау арқылы жаңа сабақты меңгеруін
ұйымдастыру. Оқушыларды жұптап жұмыстандыра отырып оларға түрткі сұрақтар қою
1. Параллелограмм анықтамасы
2. Параллелограмның қасиеттері
3. Параллелограмның белгілері
4. Параллелограмның периметрін табатын формула
Оқушылармен бірге сабақтың мақсатын құру.
Оқушылар жұптаса отырып қойылған сұрақты оқулық арқылы еске түсіріп талдау жасайды.
Сабақтың мақсатын құрады.
Жұппен жұмыстана отырып диалогтық оқыту модулі бойынша жұмыстанады, зертеушілік әңгіме, топтық әңгіме, жоғары деңгейлі сұрақтар беру.
Ромбының анықтамасын қасиеттері мен белгілерін қарастыру. Оқушыларға сұрақ қойып ромбының қасиеттерін айтқызу.
1. Ромбының қарама - қарсы бұрыштары тең
2. Ромбының бір қабырғасына іргелес бұрыштарының қосындысы 180 0 қа тең.
3. Ромбының диагональдары қиылысу нүктесінде тең екіге бөлінеді
4. Ромбының диагональі оны өзара тең екі үшбұрышқа бөледі.
Ромбының белгілерін өздеріне дәлелдету, есептер шығарту №41-44 ауызша, №48, 51, 97, 98
Жұппен талдау жасап, бір-біріне түсіндіреді, сұрақтарға жауап береді, ойларын А3 форматына түсіреді, әр жұп өз постерін қорғайды. Ромбының қасиеттері мен белгілерін өздері зертеушілік әңгіме жасай отырып дәлелдейді, дұрыс дәлелдемені дәптерге барлық оқушылар түсіреді.
Есептер шығарады: №41-44 ауызша
I жұп № 97
II жұп №48
Жұпта шығарып, есепті талдайды, қарсы жұп қателерін түзетеді.
№48, 51, 97, 98 барлығы бірге орындайды, өзара бағалайды. Бағдаршам әдісін қолданады.
Арасындағы айырмашылық салыстырады; ыстық орындық әдісі бойынша сұрақтар беріледі.
№98, 110, 51 (2)
Арасындағы айырмашылықты көрсету үшін салыстырады.
Өзара және өзін-өзі бағалау арқылы бағалау парағын толтырады.
Ыстық орындық әдісі бойынша сұрақтарға жауап береді. №98, 110, 51(2)
№46. Тіктөртбұрыштың қабырғаларының орталары ромбының төбелері болатынын дәлелдеңдер.
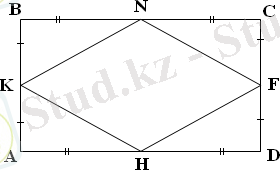
Берілгені: АВСД тіктөртбұрыш
АК=ВК, BN=NC, CF=
Дәлелдеу керек: KNFH-ромб
Дәлелдеуі: Екі катеттерінің теңдігі бойынша ΔNBK=ΔNCF=ΔHДF=ΔНАК .
Онда бұл үшбұрыштардың гипотенузалары да тең. KN=NF=FH=KH қабырғаларының теңдігі бойынша төртбұрыш KNFH-ромб болады.
№47.
A
B
C
D
O
Берілгені:
<АВО-<ВАО=15 0
Табу керек: <АВС,
Шешуі: ΔАОВ- тік бұрышты үшбұрыш
<ВАО+<АВО=90 0
<АВО-<ВАО=15 0
2<АВО =105 0
2<АВО=<АВС
<АВС=105 0
Жауабы: 75 0 және 105 0
№49.
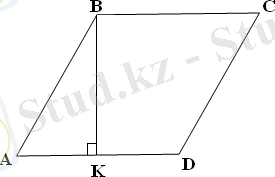
Берілгені: АВСД ромб
Табу керек: <А, <АВС-?
Шешуі: ΔАКВ- тік бұрышты үшбұрышта
Жауабы: 60 0 және 120 0
№51.
Қабырғасы және диагоналі бойынша ромб салыңдар
Салу жолы: 2 жағдай қарастырамыз. d 1 =
1. е сәулесін саламыз
2. сәуледен
3.
4.
5.
6.
7.
8.
Ромб екенін дәлелдейміз. Салуымыз бойынша
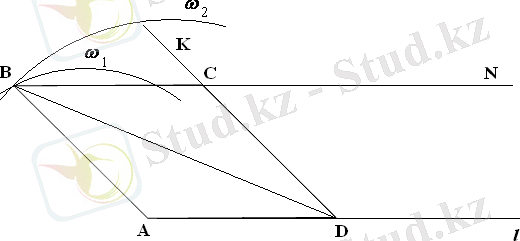
ІІ жағдай d 1 =АС диагональі болса
- е сәулесін саламыз
- сәуледен=а кесіндісін өлшеп саламыз
- шеңбер саламыз, С€
- жүргіземіз
- жүргіземіз
- ізделінді ромб
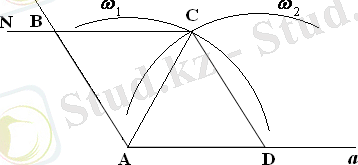
№97
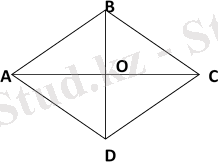
Берілгені:
<АВО:<ВАО=4:5 <ВАО+<АВО=90 0 ; <АВО:<ВАО=4:5 <АВО= 4* <ВАО/5
Табу керек: <А, <В-? 4* <ВАО/5+ <ВАО =90 0 4* <ВАО+5<ВАО=450 0 9 <ВАО=450 0
<ВАО=50 0 олай болса, <А=50 0 *2=100 0 ; <АВО=4*50 0 /5=40 0 <В=80 0
Жауабы: 80 0 және 100 0
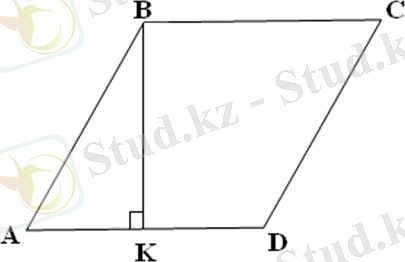
№98
Берілгені: АВСД ромб Шешуі: P=4a, a=16/4=4 олай болса, АВ=4см,
P=16 см, h=2см ΔАВК тікбұрышты үшбұрыш, ВК=1/2AB, болғандықтан <А=30 0 , олай болса <С=30 0
Табу керек: <А, <В-? Сондықтан <В=(360 0 -60 0 ) /2=150, олай болса <C=150 0
Жауабы: 30 0 және 150 0
№54.
O
Берілгені: АВСD ромб
АС=ВD
Дәлелдеу керек: АВСD квадрат
А D
Дәлелдеуі: <А=<В=90 0 екенін дәлелдеу керек. АВСD ромб болғандықтан ВD
Ал, <ВАD=2<ВАО=90 0
<АВС=2<АВО=90 0 дәлелденді
№56. Егер квадраттың қабырғасы 4, 5 см-ге ұзарса, онда берілген квадраттың периметрі қалай өзгереді?
Шешуі: Берілген квадраттың қабырғасы а десек
Р=4а а 1 =а+4, 5
Р 1 =4а 1
Р 1 =4(а+4, 5) =4а+18=Р+18
Р 1 =Р+18
Жауабы: 18 см ұзарады
4) 2 есе қысқарса ше
Р=4а а 1 =
Р 1 =4а 1 =4∙
Р 1 =
Жауабы: периметрі екі есе қысқарады.
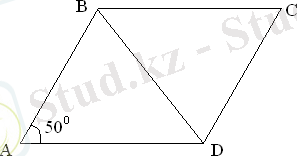
Берілгені:
Табу керек:
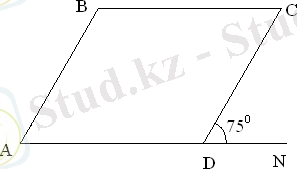
Берілгені:
Табу керек:
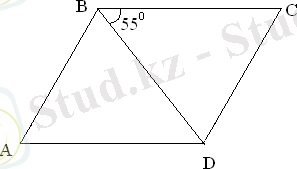
Берілгені:
Табу керек :
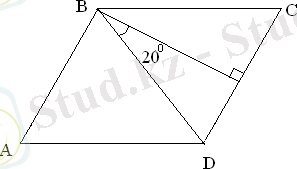
Берілгені:
Табу керек:
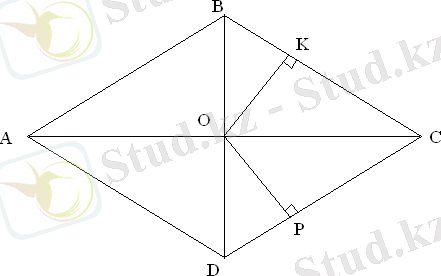
Берілгені:
ОК
Д/к: ОК=ОР
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz