11-сынып математика сабағы: интеграл көмегімен фигуралардың ауданын және айналу денелерінің көлемін есептеу

Скачать

Дайындаған :Батыс-Қазақстан облысы, Тасқала ауданы, Ы. Алтынсарин атындағы ЖББО мектептің І-санатты математика пәні мұғалімі Ташенова Гульнара Ұзақбайқызы.

11 «А» сыныбында өткізілген сабағымды ұсынып отырмын.

Тақырып: Интеграл көмегімен фигураның ауданын және көлемін есептеу.

Мақсаты:
Білімділік -оқушылардың алғашқы функция және интеграл туралы білімдерін жүйелеу, қорытындылау; алған теориялық білімдерін іс-жүзінде пайдаланып дұрыс шешім қабылдай білуге дағдыландыру;
дамытушылық -оқушылардың еркін ойлау, есте сақтау қабілеттерін дамыту;
тәрбиелік -оқушыларды ұқыптылыққа, іскерлікке, дәлдікке тәрбиелеу.

Сабақтың барысы:

І Ұйымдастырушылық кезең.

ІІ «Миға шабуыл» - қызығушылық ояту кезеңі.

ІІІ «Қатені тап!»

ІV «Білгенге маржан»- фронтальды жұмыс.

V Интерактивтік тақтамен жұмыс.

VІ «Біліміңді сынап көр!»-деңгейлік тапсырмалар.

VІІ Үйге тапсырма беру.

VІІІ Оқушыларды бағалау, сабақты қорытындылау.

І Ұйымдастырушылық кезең.

Оқушыларды түгелдеу, сабақтың мақсатымен таныстыру.

ІІ «Миға шабуыл» - қызығушылық ояту кезеңі. . (Тақтаға 2 оқушы шақырылады. )

№

Берілген функция

Алғашқы функциясы

№: 1

Берілген функция: у=k (k - тұрақты)

Алғашқы функциясы: kx +C

№: 2

Берілген функция: у= х ⁿ

Алғашқы функциясы:

№: 3

Берілген функция: у=

Алғашқы функциясы: lnx +C

№: 4

Берілген функция: у= cos x

Алғашқы функциясы: sin x +C

№: 5

Берілген функция: у= sin x

Алғашқы функциясы: - cos x +C

№: 6

Берілген функция: у=

Алғашқы функциясы: tg x +C

№: 7

Берілген функция: у=

Алғашқы функциясы: ctg x +C

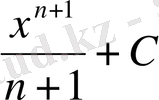
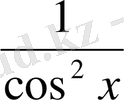
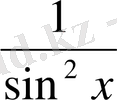
ІІІ «Қатені тап!» . (Тақтаға 2 оқушы шақырылады. )

№

Сұрақ

Дұрыс жауап

№: 1

Сұрақ: Анықталмаған интегралды табу формуласы

Дұрыс жауап:

№: 2

Сұрақ: Ньютон-Лейбниц формуласы

Дұрыс жауап:

№: 3

Сұрақ: Қисықсызықты трапецияның ауданын есептеу формуласы.

Дұрыс жауап:

№: 4

Сұрақ: Айналу денесінің көлемін есептеу формуласы.

Дұрыс жауап:

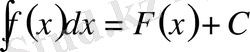
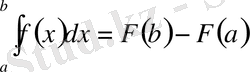
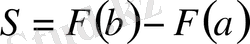
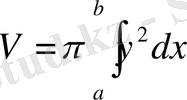
ІV «Білгенге маржан» - фронтальды жұмыс. (Тақтаға 3 оқушы шақырылады. )

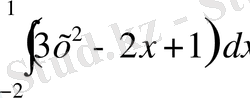
1 2

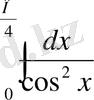
3

V Интерактивтік тақтамен жұмыс.

Тапсырма 1
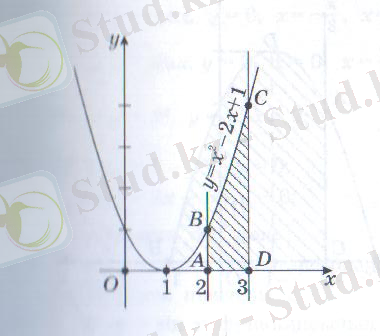
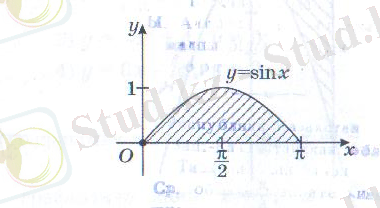
Берілген қисықтармен шектелген фигураның ауданын табыңдар:

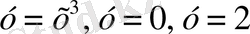
(Оқушы интерактивтік тақтада суреттеп, орындайды)

Тапсырма 2
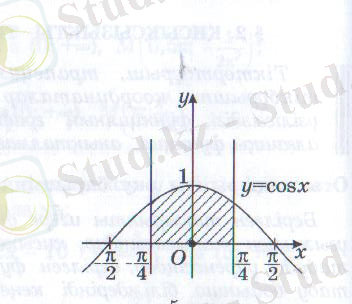
Сурет бойынша берілген қисықсызықты трапецияның ауданын есептеңіз:

І нұсқа

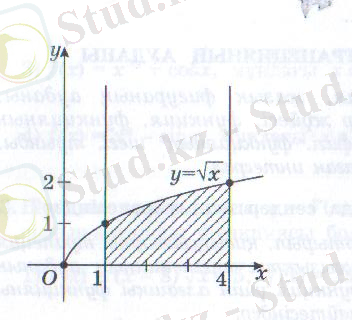
ІІ нұсқа

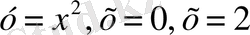Тапсырма 3
Берілген қисықтармен шектелген фигураны абсцисса осіне қатысты айналдырғанда шыққан дененің көлемін есептеңдер:

VІ «Біліміңді сынап көр!» (деңгейлік тапсырмалар. )

№

«5»

«4»

«3»

№: 1

«5»:

Берілген қисықтармен шектелген фигураның ауданын табыңдар:

у = х ² , у = 3-х

«4»: Сурет бойынша берілген қисықсызықты трапецияның ауданын есептеңіз:

«3»:

Берілген қисықтармен шектелген фигураның ауданын табыңдар:

у = х ² , х=1, х=2, у=0

№: 2

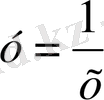«5»: гиперболасын абсцисса осіне қатысты айналдырғанда пайда болған дененің х=1 нүктесінен х =3 нүктесіне дейінгі аралықтағы дененің көлемін табыңдар.

«4»:

Берілген қисықтармен шектелген фигураның ауданын табыңдар:

у = 2х ² , у = 4х

«3»: Сурет бойынша берілген қисықсызықты трапецияның ауданын есептеңіз:

VІІ Үйге тапсырма беру.

VІІІ Оқушыларды бағалау, сабақты қорытындылау.

• Іс жүргізу
• Автоматтандыру, Техника
• Алғашқы әскери дайындық
• Астрономия
• Ауыл шаруашылығы
• Банк ісі
• Бизнесті бағалау
• Биология
• Бухгалтерлік іс
• Валеология
• Ветеринария
• География
• Геология, Геофизика, Геодезия
• Дін
• Ет, сүт, шарап өнімдері
• Жалпы тарих
• Жер кадастрі, Жылжымайтын мүлік
• Журналистика
• Информатика
• Кеден ісі
• Маркетинг
• Математика, Геометрия
• Медицина
• Мемлекеттік басқару
• Менеджмент
• Мұнай, Газ
• Мұрағат ісі
• Мәдениеттану
• ОБЖ (Основы безопасности жизнедеятельности)
• Педагогика
• Полиграфия
• Психология
• Салық
• Саясаттану
• Сақтандыру
• Сертификаттау, стандарттау
• Социология, Демография
• Спорт
• Статистика
• Тілтану, Филология
• Тарихи тұлғалар
• Тау-кен ісі
• Транспорт
• Туризм
• Физика
• Философия
• Халықаралық қатынастар
• Химия
• Экология, Қоршаған ортаны қорғау
• Экономика
• Экономикалық география
• Электротехника
• Қазақстан тарихы
• Қаржы
• Құрылыс
• Құқық, Криминалистика
• Әдебиет
• Өнер, музыка
• Өнеркәсіп, Өндіріс