Құрамында дәрежелері бар өрнектерді түрлендіру. 7-сынып
Трекин орта жалпы білім беретін қазақ мектебі
Ашық сабақтың тақырыбы:
Құрамында дәрежелері бар өрнектерді түрлендіру
7 ә сыныбы
Пән мұғалімі: Габдуллина А. А.
2014 - 2015 оқу жылы
Сабақтың тақырыбы: Құрамында дәрежелері бар өрнектерді түрлендіру.
Сабақтың мақсаты:
Білімділік: Құрамында дәрежелері бар өрнектерді түрлендіру бойынша алған білімдерін жалпылап, тиянақтау , қосымша мәліметтер беру.
Дамытушылық : Тиімді әдіс- тәсілдер арқылы оқушылардың ой- өрісін кеңейту, өздігінен жұмыс жасау, іздену, шығармашылық қабілеттерін дамыту.
Тәрбиелік : Оқушыларды нақтылыққа, ұйымшылдыққа, ұқыптылыққа, дәлдікке тәрбиелеу.
Сабақтың типі : Білімді бекіту сабағы.
Сабақтың әдіс- тәсілдері : графикалық диктант, ауызша есептер шығару, өзіндік ізденіс (тарихи мағлұмат), деңгейлік тапсырмалар.
Көрнекілігі: карточкалар, нақыл сөз, кестелер.
Күтілетін нәтиже: Құрамында дәрежелері бар өрнектерді түрлендіру бойынша есептерді шығаруда формулаларды дұрыс қолдана алады, жауабын дұрыс есептеп шығара алады.
Сабақтың барысы :
І. Ұйымдастыру кезеңі : оқушыларды түгендеу, сабаққа әзірлігін тексеру.
ІІ. Үй тапсырмасын тексеру:
ІІІ. Өтілген материалдың игерілуін тексеру :
1. Графикалық диктант: иә- жоқ
- Негіздері бірдей дәрежелерді бөлгенде негізін өзгеріссіз қалдырып, бөлінгіштің дәреже көрсеткішін бөлгіштің дәреже көрсеткішіне қосамыз (азайтамыз)
- (а 3 ) 2 = а 5 тең (а 6 )
- (- 3х 2 у 8 ) 2 = 9х 4 у 16
- Дәрежені дәрежеге шығарғанда, негізін өзгертпей дәреже көрсеткіштері қосылады.
- 3
-5
∙ 3
3
=
тең (
)
- Бөлшекті дәрежеге шығарғанда, оның аламының да, бөлімінің де әрбір көбейткішін осы дәрежеге шығарады.
- (2999+ 3001) 0 = 6000 -ға тең?
- Негіздері бірдей дәрежелерді көбейткенде, олардың дәреже көрсеткіштерін қосып, негіздерін өзгеріссіз қалдырамыз .
- (-а) 10 ∙ а 5 ∙ (- а) 3 = а 18 (- а 18 )
2. Ауызша есептер шығару арқылы жасырылған сөйлемді тауып, мағынасын ашу:
(а 6 х 2 ) 3 (Б) 1, 4с 4 ∙20с 10 (І) 3а 5 в 5 ) 2 (Л) 7с 8 (2с 3 ) 2 (І) (2а 2 х) 3 (М)
10
2
- 5
2
(
Қ)
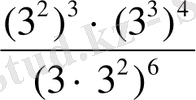(А)
(7-9)
5
∙125
0
(З) х
12
∙ (х
2
)
3
(Ы)
3 а 3 ∙ (-ав 2 ) 4 (Н ) х 5 :(х∙х 4 ) (А)
«БІЛІМ- ҚАЗЫНА»
ІҮ. Тарихи деректерге шолу:
- Ұлы грек математигі Пифагор санның натурал көрсеткішті дәрежесін қандай да бір фигура түрінде көрсетуге болатындығын анықтаған.
2 2
•
•
•
•
3 2
•
•
•
•
•
•
•
•
•
4 2
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
- Ағылшын математигі С. Стивин санды дәреже түрінде жазуды ойлап тапты: 3(3) + 5(2) - 4 . Қазіргі кездегі түрі:33+ 52- 4
- Дәрежені ең көп қолданатындар астрономдар. Олар әр қадамдарында алып сандармен кездеседі және олармен есептеулер жүргізеді. Мысалы: Андормеда тұмандығына дейінгі ара қашықтық 95 км, Күн массасы жуықтап алғанда 2 кг. Осындай алып сандарды жазу, есептеу қиындыққа соғады. Сондықтан санды стандарт түрде жазуды қолданады. км икг. Сонымен қатар дәрежені биологтар, химиктер де қолданады.
- Ертеде Ежелгі славяндықтар алып сандарды жаза білген, олардың арнайы атаулары болған:
«тысяща» =
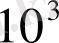, «тьма» =
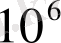, «легион» =
,
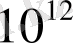«леодр» =
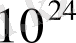, «ворон» =
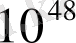, «колода» =
.
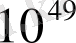Ү. Білімді бекіту:
1. Деңгейлік тапсырмалар:
І- деңгей: « 3 »
1. Өрнектің мәнін тап:
24 ·с
-3
, мұндағы с =
.
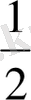2. Амалды орында:
а) (х
7
)
3
· х
12
;
б) х
-12
: х
3
;
в) ( 3 х
6
)
3
;
3. k- ның қандай мәнінде теңдік дұрыс болады : 5 8 : 5 k = 5 4
ІІ деңгей: « 4 »
Есепте :
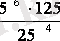
ІІІ деңгей: « 5 »
х-ті тап:
х
2
6
2
9
= 2
17
5 тапсырма- “5” 4 тапсырма - “4” 3 тапсырма- “3”
ҮІ. Қорытындылау :
1. «Ой толғаныс»: Бүгінгі сабақтан не алдым?
2. Өзара бағалау: Оқушылармен бірігіп оқушы білімін бағалау.
Бағалау парағы
Аты- жөні
3. Үй тапсырмасы: Құрамында дәрежелері бар өрнектерге есептер құрастыру.
1. Графикалық диктант: иә- жоқ
- Негіздері бірдей дәрежелерді бөлгенде негізін өзгеріссіз қалдырып, бөлінгіштің дәреже көрсеткішін бөлгіштің дәреже көрсеткішіне қосамыз (азайтамыз)
- (а 3 ) 2 = а 5 тең (а 6 )
- (- 3х 2 у 8 ) 2 = 9х 4 у 16
- Дәрежені дәрежеге шығарғанда, негізін өзгертпей дәреже көрсеткіштері қосылады.
- 3
-5
∙ 3
3
=
тең (
)
- Бөлшекті дәрежеге шығарғанда, оның аламының да, бөлімінің де әрбір көбейткішін осы дәрежеге шығарады.
- (2999+ 3001) 0 = 6000 -ға тең?
- Негіздері бірдей дәрежелерді көбейткенде, олардың дәреже көрсеткіштерін қосып, негіздерін өзгеріссіз қалдырамыз .
- (-а) 10 ∙ а 5 ∙ (- а) 3 = а 18 (- а 18 )
1. Графикалық диктант: иә- жоқ
- Негіздері бірдей дәрежелерді бөлгенде негізін өзгеріссіз қалдырып, бөлінгіштің дәреже көрсеткішін бөлгіштің дәреже көрсеткішіне қосамыз (азайтамыз)
- (а 3 ) 2 = а 5 тең (а 6 )
- (- 3х 2 у 8 ) 2 = 9х 4 у 16
- Дәрежені дәрежеге шығарғанда, негізін өзгертпей дәреже көрсеткіштері қосылады.
- 3
-5
∙ 3
3
=
тең (
)
- Бөлшекті дәрежеге шығарғанда, оның аламының да, бөлімінің де әрбір көбейткішін осы дәрежеге шығарады.
- (2999+ 3001) 0 = 6000 -ға тең?
- Негіздері бірдей дәрежелерді көбейткенде, олардың дәреже көрсеткіштерін қосып, негіздерін өзгеріссіз қалдырамыз .
- (-а) 10 ∙ а 5 ∙ (- а) 3 = а 18 (- а 18 )
1. Графикалық диктант: иә- жоқ
- Негіздері бірдей дәрежелерді бөлгенде негізін өзгеріссіз қалдырып, бөлінгіштің дәреже көрсеткішін бөлгіштің дәреже көрсеткішіне қосамыз (азайтамыз)
- (а 3 ) 2 = а 5 тең (а 6 )
- (- 3х 2 у 8 ) 2 = 9х 4 у 16
- Дәрежені дәрежеге шығарғанда, негізін өзгертпей дәреже көрсеткіштері қосылады.
- 3
-5
∙ 3
3
=
тең (
)
- Бөлшекті дәрежеге шығарғанда, оның аламының да, бөлімінің де әрбір көбейткішін осы дәрежеге шығарады.
- (2999+ 3001) 0 = 6000 -ға тең?
- Негіздері бірдей дәрежелерді көбейткенде, олардың дәреже көрсеткіштерін қосып, негіздерін өзгеріссіз қалдырамыз .
- (-а) 10 ∙ а 5 ∙ (- а) 3 = а 18 (- а 18 )
1, 4с 4 ∙20с 10 (І) 3а 5 в 5 ) 2 (Л) (2а 2 х) 3 (М) 7с 8 (2с 3 ) 2 (І) (а 6 х 2 ) 3 (Б)
10
2
- 5
2
(
Қ)
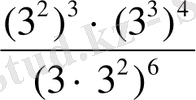(А)
(7-9)
5
∙125
0
(З)
х
12
∙ (х
2
)
3
(Ы)
х 5 :(х∙х 4 ) (А) 3 а 3 ∙ (-ав 2 ) 4 (Н )
1, 4с 4 ∙20с 10 (І) 3а 5 в 5 ) 2 (Л) (2а 2 х) 3 (М) 7с 8 (2с 3 ) 2 (І) (а 6 х 2 ) 3 (Б)
10
2
- 5
2
(
Қ)
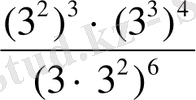(А)
(7-9)
5
∙125
0
(З)
х
12
∙ (х
2
)
3
(Ы)
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.
Ақпарат
Қосымша
Email: info@stud.kz